-

人教版新课标小学数学三年级下册用连乘解决问题说课稿2篇
3、小结比较观察三种方法,提出问题:为什么同一个问题有三种不同的解决方法?学生交流,教师小结:先解决的问题不同,选择的信息不同,图形拼摆的不同,解决的方法就不同,体现数形结合的思想。相同点是:无论思路如何,都是用连乘的方法解决问题。板书课题:解决问题——两步连乘应用题生活中还有很多这样的清况,想不想再尝试一下。(三)联系生活,优化方法,拓展深化,学校有特异为这些参加比赛的同学们购买了矿泉水,出示画面:共有20箱矿泉水,每箱24瓶,每瓶2元,请问学校共要支付多少钱?学生独立完成观察和思考的角度不同,先后选择的信息不同,所以同一道题有不同的解决方法。看来大家多用连乘的方法解决问题有了进一步的理解。生活中类似这样的问题很多,再来看一看:学校定好了水,付了钱,总得运回来吧.出示搬运车搬水到卡车上的画面:搬运车一次搬4摞,一摞3箱,一箱24瓶,请问搬运车一次能搬多少瓶?

人教版新课标小学数学四年级上册商的变化规律说课稿2篇
第三个规律,商不变的规律。这是本课的重点内容。有了两次的探究经验,这一规律的学习与理解,可以完全放手让学生自主进行。猜想如果商不变,被除数、除数会发生什么变化呢?学生根据已有的经验,可能会有不同猜想,我要求学生带着问题通过计算、观察、比较、主动探讨总结出:被除数和除数同时扩大(或缩小)相同的倍数(0除外)商不变。利用合作学习,通过动脑动口动手,既提高学生解决问题的学习能力,又培养了合作学习的意识和习惯。给学生提供展示研究成果的机会,体验成功。需要教师提醒的是“有没有被除数和除数同时乘或除以不相同的数,商也不变的?”学生举反例加以说明并指出“相同的倍数不包括0”。设计这个环节,也有意让学生去验证商不变性质。学生在表述时,对于逻辑的严密性和语言的完整性需要老师及时指导,在突出重点的同时培养学生的语言表达能力。整个环节在验证的基础上,步步深化商的变化规律,为学生应用新知做好铺垫。

人教版新课标小学数学四年级上册口算乘法说课稿2篇
2、创设学生熟悉的生活情境,探究新知首先,我让学生说一说教材45页的情境图,反映的是什么内容?谁来读一读6副图的信息,让学生观察,使学生初步理解“速度”的含义。接着让学生说一说自己了解的其他交通工具的速度。让学生说你是怎样读速度的,接下来点播速度的写法。为以后的速度、时间、路程三者的关系打下基础。3、自主探究,学习新知教师提供信息:,人骑自行车1小时大约可以行16千米,3小时可以行多少千米?让学生根据这个信息列出算式,再要求学生用自己已有的知识经验独立口算,交流算法得出计算结果。为了检查学生掌握的情况和语言的表达能力我出示以下4个小题。18×4=、24×3=、25×2=、14×6=4、交流汇报,建构知识由学生汇报不同的算法过程,引导学生对比不同算法的特点,确定最优化的算法。

人教版新课标小学数学四年级上册田忌赛马说课稿2篇
(四)深入探究,重新审视对策问题解决问题不是学习的最终目的,让学生不断体验对策的价值才是关键所在。对策的价值在哪里?设计对策的关键是什么?把问题抛给学生去思考,一方面让学生再次感受正确对策达到“以小打大”、“以弱胜强”妙处,更重要的是让学生明确设计对策的关键前提是什么?即“知己知彼,百战不殆”的数学思想,以便根据对手的变化灵活运用对策。教学步骤设计:1、学生探讨,如果齐王的下等马都比田忌的上等马快,田忌还有获胜的可能吗?2、田忌赛马第二次获胜的前提是什么?(田忌猜测道齐王安排赛马的出场顺序还和第一次一样)3、如果齐王安排赛马的出场顺序改变了,田忌该怎样才能获得胜利?(找两位同学分角色演示一下)4、回忆课前时候,老师为什么会在纸牌游戏“比大小中”屡战屡胜。

人教版新课标小学数学四年级下册营养午餐说课稿2篇
“营养午餐”是学生既熟悉又陌生的一个课题,熟悉的是学生每天都必须接触,陌生的是学生对于什么样的搭配才是合乎营养标准的“营养午餐”还没有达到科学合理的认识,偏食挑食等不良饮食习惯在学生群体中比比皆是。教材结合学生的生活实际,围绕午餐的营养问题设计了几个数学综合应用活动:首先是民主路小学为学生提供的三种午餐菜谱;其次是营养专家介绍了10岁儿童营养午餐的两个基本指标;接着是让学生尝试合理搭配自己喜欢的午餐菜谱,最后通过统计、排列组合,让学生运用所学知识,解决问题。一方面使学生综合运用简单的排列组合,统计等相关知识解决问题,体会数学在日常生活中的应用价值,增强学生应用数学的意识,另一方面通过了解各份菜中热量、脂肪、蛋白质的含量和营养午餐的一些基本指标,促使学生克服偏食、挑食的毛病,养成科学的饮食习惯。

人教版新课标小学数学五年级上册稍复杂的方程说课稿2篇
一、说教材:稍复杂的方程的教学任务例1教学解方程ax±b=c及其应用(列方程解形如ax±b=c的问题)(1)把解方程和用方程解决问题有机结合,在解决问题的过程中解较复杂的方程。(2)结合现实素材(足球上两种颜色皮的块数)引出,这种问题用算术方法解决思考起来比较麻烦。(3解方程的过程其实是由解若干基本方程构成的(y-20=4,2x=24),需要强调把2x看成一个整体。(4)可以列出不同的方程,如2x-4=20,关键是使学生理解数量关系。二、说学生:学生在前面已经学习了简单的方程数量关系,及简单方程式的解法,而且我在前面的教学中已经笨鸟先飞,让学生接触了形如:ax±b=c的方程式。三、说教法:根据学生的实际情况,我准备在教学过程中,重点讲解稍复杂方程式的数量关系式的分析研究,让学生根据应用题的题意列出正确的数量关系式。

人教版新课标小学数学五年级下册粉刷围墙说课稿2篇
还有一点思考是作为教师应该有这样一种认识,学生从自己的头脑中搜索有价值的数学知识储备,并对这些知识储备进行筛选和取舍,这是一种重要的能力。换句话讲,这就是学生分析问题和解决问题的能力,这种能力是需要培养的,这也是在第二学段“综合应用”中必须把握的准则。教学目标:1、让学生经历粉刷围墙的实践活动,巩固长方体表面积的计算方法,加强数学知识在实际生活中的应用。2、通过活动,培养学生收集、分析信息的意识和能力,使学生能根据实际情况,选择合理方案。3、让学生体验数学知识与生活的紧密联系,并利用数学知识科学地指导生活,感受成功。教学重点:整理分析和比较信息,制定方案。教学难点:策略的优化。教学准备:课前做好相关数据收集整理的准备工作,教师尤其要在课前了解学生调查的涂料价目。学生准备:计算器,记录纸等。

人教版新课标小学数学五年级下册容积和容积单位说课稿2篇
3. 实验(课件演示)每个人每天要喝1400毫升水,也就是1.4升,让同学们猜出猜看能有几杯水,通过实验告诉学生每天至少要喝多少杯水。(课件演示)阅读材料,对学生进行节约用水的思想教育。4. 教师:我们知道了容积和容积单位,也知道了它们与体积单位的关系,现在让我们试一试怎样计算一个容器的容积.出示例5、一种小汽车上的油箱,里面长5dm,宽4dm,高2dm。这个油箱可以装汽油多少升?请一位同学读题.教师:这道题告诉了我们油箱里面的长、宽、高,我们能不能计算出它的容积?(可以.)但是,我们能不能直接算出它的容积是多少升?(不能.)那么应该怎样做?(先算出体积,再把算出的体积单位的名数改写成容积单位的名数.)教师让学生独立做题,教师行间巡视,做完后一步一步地指名让学生说一说是怎么做的,集体订正。

人教版新课标小学数学五年级下册体积和体积单位说课稿2篇
5、 你能结合刚才的活动说一说你的感受吗?6、 看来物体所占空间还有大小之分,那你能判断出手机、收音机哪个物体所占的空间大?哪个物体所占的空间小吗?7、 象石块、手机、书包等这些都是它们的体积,谁能根据你的理解说一说什么是物体的体积?[小学生的思维以形象思维为主,随着年龄的增长逐步向抽象思维过渡。根据这一特点,我在学生感知“空间”的基础上,通过三次摸一摸的活动,引导学生进行操作、观察,思考,使操作、观察与思维、语言表达紧密结合起来,然后再逐步摆脱直观形象,利用表象逐步抽象形成概念,由感性认识上升到理性认识。](三) 尝试、解决问题在新一轮课改中,《标准》所提倡的数学课堂教学应“由单纯的传授知识的殿堂转变为学生主动从事数学活动的场所;学生从单纯的知识接受者转变为数学学习的主人。”

人教版新课标小学数学六年级下册比例尺说课稿2篇
一、说教材:我说课的内容为六年级下册的《比例尺》。这节课是在学生学完“比例的意义和基本性质”、“正、反比例的意义”后安排的内容。这部分内容是学生学习有关地图、工程图纸的计算的基础。比例尺在生活中也有广泛应用,学好它也很有现实意义。 教学目标1、知识与技能:使学生理解比例尺的意义,学会求比例尺,图上距离和实际距离。2、过程与方法:使学生经历比例尺产生过程和探究比例尺应用的过程,提高学生解决实际问题的能力。3、情感态度和价值观:结合具体情境,使学生体验到数学与生活的密切联系,进一步激发学生学习数学的兴趣。重点:理解比例尺的概念,根据比例尺的意义求比例尺、实际距离和图上距离。难点:从不同的角度理解比例尺的意义二、说学生: 六年级的下学期的学生,对于各种图形有着丰富的生活经验,所以,讲解有关比例尺的知识,学生有感性认识,同时也会饶有兴趣的。

人教版新课标小学数学六年级下册邮票中的数学问题教案
《贴邮票》活动要求:A、每组4人,给四封不同地点、质量的信件B、根据信封上的信息计算邮费并按要求贴上邮票(邮票的总面值刚好等于邮费,不能多贴)每封信最多贴三张邮票,只有0.8元或1.2元的两种邮票纪律要求:看看哪组合作得最好,速度最快!如果遇到困难,在事发那个在一边最后再去解决。3、小组汇报(1)、贴邮票的过程中大家遇到了什么问题?(有的能贴有的不能贴)这样的信件有哪些?(告诉我地点、质量、邮费)(2)、其他的信件都能贴出来嘛?说说看你是怎么贴邮票的?(3)、请将你们贴好邮票的信件送到邮箱来。剩下的都是一些“难题”(4)、思考:为什么4.0元、4.8元、6元的邮费没有办法按要求贴出邮票?(5)、原因出在哪里?这个问题怎么解决?(邮票面值太小,将邮票的面值改大)(6)、那最少要改成多大的?为什么?(将邮票面值改大,你会从多大面值的邮票开始考虑?为什么?)

疫情后高级中学校长在新学期开学典礼上的讲话
回望2020年,令人感慨万千。这一年,面对肆虐的新冠疫情,全国人民众志成城,取得抗疫斗争重大战略成果;这一年,我国经济逆风前行,走出V字形复苏曲线,中国成为全球唯一实现正增长的主要经济体;这一年,中国如期完成脱贫攻坚目标任务,提前十年完成笔扫千军整理联合国减贫目标;这一年,学校秉持“融教育”办学理念,稳步推进教育质量提升工程,高级中学一本上线38人,本科上线330人;初级中学中招500分以上22人,450分以上68人,教育教学质量在全市同类学校中名列前茅;

疫情后高级中学校长在新学期开学典礼上的讲话发言.
成绩属于过去,它更是鞭策我们前进的动力,逆水行舟,不进则退。新的学期,孕育着新的希望和憧憬,我们的每一位老师和同学,在经过一个寒假的短暂休息与调整之后,又将满怀信心、斗志昂扬地站在新学期的起跑线上,为实现理想目标而全身心投入工作和学习。
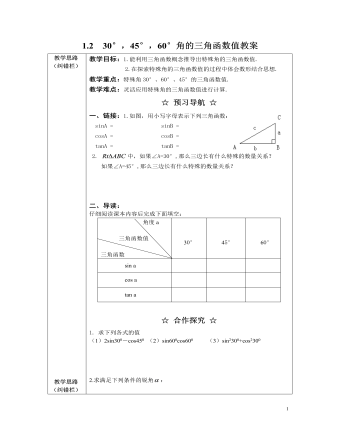
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中七年级数学上册代数式的求值教案2
解 由题意可得,今年的年产值为a·(1+10%) 亿元,于是明年的年产值为a·(1+10%)·(1+10%)= 1.21a(亿元).若去年的年产值为2亿元,则明年的年产值为1.21a =1.21×2 = 2.42(亿元).答:该企业明年的年产值将能达到1.21a亿元.由去年的年产值是2亿元,可以预计明年的年产值是2.42亿元.例3 当x=-3时,多项式mx3+nx-81的值是10,当x = 3时,求该代数式的值.解 当x=-3时,多项式mx3+nx-81=-27m-3n-81, 此时-27m-3n-81=10, 所以27m+3n=-91.则当x=3,mx3+nx-81 =( 27m+3n )-81=-91-81=-172.注:本题采用了一种重要的数学思想——“整体思想”.即是考虑问题时不是着眼于他的局部特征,而是把注意力和着眼点放在问题的整体结构上,把一些彼此独立,但实质上又相互紧密联系着的量作为整体来处理的思想方法.

北师大初中七年级数学上册有理数乘法的运算律教案2
分析:(1)(2)用乘法的交换、结合律;(3)(4)用分配律,4.99写成5-0.01学生板书完成,并说明根据什么?略例3、某校体育器材室共有60个篮球。一天课外活动,有3个班级分别计划借篮球总数的 , 和 。请你算一算,这60个篮球够借吗?如果够了,还多几个篮球?如果不够,还缺几个?解:=60-30-20-15 =-5答:不够借,还缺5个篮球。练习巩固:第41页1、2、7、探究活动 (1)如果2个数的积为负数,那么这2个数中有几个负数?如果3个数的积为负数,那么这3个数中有几个负数?4个数呢?5个数呢?6个数呢?有什么规律? (2)逆用分配律 第42页 5、用简便方法计算(三)课堂小结通过本节课的学习,大家学会了什么?本节课我们探讨了有理数乘法的运算律及其应用.乘法的运算律有:乘法交换律:a×b=b×a;乘法结合律:(a×b)×c=a×(b×c);分配律:a×(b+c)=a×b+a×c.在有理数的运算中,灵活运用运算律可以简化运算.(四)作业:课本42页作业题

北师大初中七年级数学上册有理数的乘方教案2
二.思考:(-2) 可以写成-2 吗?( ) 可以写成 吗?(指名学生回答,师生共同总结:负数和分数的乘方书写时,一定要把整个负数和分数用小括号括起来)三.计算:①(-2) ,②-2 ,③(- ) ,④ (叫4个学生上台板演,其他练习本上完成,教师巡视,确保人人学得紧张高效).(四)讨论更正,合作探究1.学生自由更正,或写出不同解法;2.评讲思考:将三题①③中将底数换成为正数或0,结果有什么规律?学生总结:负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都为0。有理数的乘方就是几个相同因数积的运算,可以运用有理数乘方法则进行符号的确定和幂的求值.乘方的含义:①表示一种运算;②表示运算的结果.

北师大初中七年级数学上册有理数的乘法法则教案2
讨论归纳,总结出多个有理数相乘的规律:几个不等于0的因数相乘,积的符号由负因数的个数决定。当负因数有奇数个时,积的符号为负;当负因数有偶数个时,积的符号为正。只要有一个因数为0,积就为0。(2)几个不等于0的因数相乘时,积的绝对值是多少?(生:积的绝对值是这几个因数的绝对值的乘积.)例2、计算:(1) ;(2) 分析:(1)有多个不为零的有理数相乘时,可以先确定积的符号,再把绝对值相乘;(2)若其中有一个因数为0,则积为0。解:(1) = (2) =0练习(1) ,(2) ,(3) 6、探索活动:把-6表示成两个整数的积,有多少种可能性?把它们全部写出来。(三)课堂小结通过本节课的学习,大家学会了什么?(1)有理数的乘法法则。(2)多个不等于0的有理数相乘,积的符号由负因数的个数决定。(3)几个数相乘时,如果有一个因数是0,则积就为0。(4)乘积是1的两个有理数互为倒数。(四)作业:课本作业题

北师大初中七年级数学上册有理数的混合运算教案2
1、掌握有理数混合运算法则,并能进行有理数的混合运算的计算。2、经历“二十四”点游戏,培养学生的探究能力[教学重点]有理数混合运算法则。[教学难点]培养探索思 维方式。【教学过程】情境导入——有理数的混合运算是指一个算式里含有加、减、乘、除、乘方的多种运算.下面的算式里有哪几种运算?3+50÷22×( )-1.有理数混合运算的运算顺序规定如下:1 先算乘方,再算乘除,最后算加减;2 同级运算,按照从左至右的顺序进行;3 如果有括号,就先算小括号里的,再算中括号里的,最后算大括号里的。 加法和减法叫做第一级运算;乘法和除法叫做第二级运算;乘方和开方(今后将会学到)叫做第三级运算。注意:可以应用运算律,适当改变运算顺序,使运算简便.合作探究——

北师大初中七年级数学上册有理数的加法法则教案2
师生共同归纳法则2、异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。生5:这两天的库存量合计增加了2吨。(+3)+(-1)=+2 或(+8)+(-6)=+2师:会不会出现和为零的情况?提示:可以联系仓库进出货的具体情形。生6:如星期一仓库进货5吨,出货5吨,则库存量为零。(+5)+(-5)=0师生共同归纳法则3、互为相反数的两个数相加得零。师:你能用加法法则来解释法则3吗?生7:可用异号两数相加的法则。一般地还有:一个数同零相加,仍得这个数。小结:运算关键:先分类运算步骤:先确定符号,再计算绝对值做一做:(口答)确定下列各题中和的符号,并说明理由:(1)(+3)+(+7);(2)(-10)+(-3);(3)(+6)+(-5);(4)0+(-5).例 计算下列各式:(1)(-3)+(-4);(2)(-2.5)+5;(3)(-2)+0;(4)(+ )+(- )教法:请四位学生板演,让学生批改并说明理由。

