-

关于六月份国旗下讲话稿的精选
尊敬的老师,同学们:大家好!今天我发言的题目是《战胜挫折,走向成功》。古人云:人生不如意,十有八九。挫折是人生的必然,是指个体在从事有目的的活动中,遇到了障碍或干扰,导致其动机不能实现,需要不能满足时产生的情绪反应。如同人生的影子,它将伴随着每一个人前进的脚步。虽然谁都期望一生中一帆风顺,事事如意,但是或早或迟,或大或小,总难免遇害上各式各样的挫折。认真准备考试,却没有得到理想的成绩;以诚待人,却换来嘲讽的目光……这些困难都会给我们造成挫折感。面对这些失败,我们会难过,会哭泣,然而,困难不会因泪水退却,人生的磨难也从来不会给出软弱的心灵让座,不能让沮丧把青春的果实泡得霉烂。是逃避,还是奋起?我想大多数人会选择后者。挫折能使人真正的保持聪明和清醒。当遇到挫折和不如意时,越是回避越难以解脱,只有敢于直面它,掌握和运用正确的方法,这才能逐渐走向成熟。

关于六一儿童节的国旗下的讲话
十六周国旗下讲话同学们:刚刚送走了五月份展能活动月,相信同学们已经从不同的方面体验到了成功的甜蜜滋味吧。紧接着的六一儿童节,更是让同学们开开心心地度过了快乐的一天吧,今年的六一恰逢与端午相连,真是幸福满盈啊!进入六月,回顾这个学期同学们对课外书的阅读一定有很多的收获吧。每周二和周四的午间阅读,是校园里最美丽的一道风景,你们在书海里遨游时专注的表情,是人间纯美的瞬间。相信你们在阅读的时候也感受到一种其他的娱乐无法替代的幸福体验吧。还记得《不一样的卡梅拉》里,卡梅拉家族的一次次探险,一回回让我们忍俊不禁的爆笑吗? 还记得在读《老鼠记者》时 ,我们仿佛在跟着杰罗尼摩一起天马行空地周游世界,经历各种惊险刺激而又妙趣横生的冒险之旅,并且总能从中找到许多快乐好玩的东西吗?

关于六一儿童节国旗下讲话参考
“六一”的太阳为什么这样辉煌?“六一”的花朵为什么这样芬芳?“六一”的红领巾为什么这样鲜艳?“六一”的孩子们为什么这样欢畅……你知道,他知道,大家全知道。全世界最年少的节日已经来到,全世界最天真的节日就在今朝。“六一”的歌声为什么这样动听?“六一”的舞蹈为什么这样多情?“六一”的故事为什么这样引人?“六一”的集会

关于六一儿童节国旗下讲话稿
五月的时光在不知不觉间流逝,六月的阳光将照耀在我们的脸上。天真的笑脸,欢快的笑声,明天我们将迎来六一国际儿童节。目前,各国政府普遍关注儿童的未来,保护儿童的权益。联合国1990年通过的《儿童权利公约》,我国是参与制定国和签约国之一。在批准《儿童权利公约》的同一年,我国颁布了《中华人民共和国未成年人保护法》,这对维护少年儿童的权益起到了积极的作用。“六一”是我们最快乐的节日,因为: 我们是家庭的宝贝,更是家庭的希望。你们能够快乐地成长,家庭就充满欢歌与笑语。我们是学校的学生,更是学校的希望。我们能够全面地发展,学校就充满生机与活力。我们是社会的未来,更是社会的希望。我们能够和谐地发展,社会就充满热情与友爱。

儿童节国旗下讲话稿:六一畅想
尊敬的各位老师、亲爱的同学们:大家早上好!我是六o一班的蔡文婷,今天,我向大家演讲的题目是《六一畅想》。再过一天,就是“六一”儿童节了,那是个充满幻想的日子,那是个令世界少年儿童欢欣鼓舞的日子。可是,回想起往年的“六一”节,不是父母带我们去逛公园,去吃“肯德基”、“麦当劳”,就是去商场购物,或参加学校举行的“六一”节晚会,游园活动……全都是按照成年人的思维方式制造隆重的节日气氛,却忽视了我们的个性,我们的心愿,爸爸、妈妈、老师、阿姨们,请松开你们的手吧,放飞笼中可怜的小鸟,让我们也在无边无际的蓝天中自由地翱翔吧!又一个盼望已久的“六一”节就要到了,她穿着五彩的霞衣,手捧着鲜花,沐浴着六月的风,踩踏着六月的雨,轻轻地,悄悄地向我们走来了。我不禁陷入了美妙的遐想之中,构思着一幅幅属于我们自己的节日图画。我期望在“六一”那一天,所有的公园免费向儿童开放,让我们像鸟儿一样尽情地玩耍,自由地飞翔。我期望在“六一”那一天,几个小伙伴去郊外野餐,倾听大自然的声音,在大自然中自制美餐,风餐露宿。我期望在“六一”那一天,老师不布置一点儿作业,让我们呼吸一下轻松的空气,家长不再给我们补课,让我们做一回自己的主人。

六一儿童节国旗下讲话演讲稿
尊敬的各位领导,各位嘉宾,亲爱的老师们,同学们:大家好!在这鲜花烂漫,绿草如茵的初夏时节,我们迎来了孩子们的盛大节日——六一国际儿童节,我非常荣幸地与小朋友们一起共度这美好的节日。值此机会,谨让我向全体小朋友、少先队员们致以诚挚的节日问候,并向辛勤耕耘、呕心沥血培育祖国花朵的园丁们致以崇高的敬意!向今天即将受到表彰的先进个人和先进集体表示热烈的祝贺!少先队员、小朋友们,我们正处于一个充满希望的挑战的新时代,你们幸运地生活在一所关注师生生存状态,追求最大限度满足师生成长需要的学校;一所以“给学生最美好的童年,给人生最坚实的起步”为核心办学理念,倾情打造“附小教育”品牌的学校;一所“以教育科研为先导的实验学校,以英语特色为核心的育才学校,以服务社会为内涵的新型学校”

货车租车合同-合同范本
一、车辆: 乙方按甲方要求,提供____座的____车____辆,允许载人数为____ 人(不含司机),超过该人数,司机有权拒载,否则所有责任由甲方负责。 二、费用:共________元 费用(________)包含、(__)不含:所有过路费、过桥费、停车费。 三、权利义务: 1.乙方根据甲方提供大概行程进行报价,如甲方实际用车,超出原计划,需根据新的行程计价,否则乙方司机有权拒载。在用车期间,甲方需负责乙方司机的食、宿(二天以上)问题。 2.为确保双方权益,甲方在确定用车时(用车前),至少支付给乙方50% 保证金________ 元,如因甲方原因,取消用车,保证金不予退还(未付保证金个人或单位,确定用车,临时变更,取消或改用车日期,需支付车款50%做误工费)。 单接送用车,甲方预约侯车时间,不能超过1小时,否则每小时另支付司机加班费¥100元;乙方司机按预约时间准时到达指定地点(迟到不能超过15分钟),否则视乙方违约,扣除¥100元,超过50分钟(非人为造成,如:道路严重堵塞、天灾人祸、车祸等),将赔偿甲方全部损失(协议租车价)。

复活节国旗下讲话稿:Happy Easter
复活节国旗下讲话稿:HappyEasterGoodmorningeverybody,whoknowsEasterDay?yes,复活节。今天,michelle要为大家介绍的是西方的重要节日——复活节。我们了解最多的可能就是christmas——圣诞节。殊不知,复活节是仅次于圣诞节的重要节日。为什么呢?在复活节期间,有什么好玩的事,好吃的东西呢?让我们来听一听Terresa喻怡宸的介绍吧!四(4)中队喻怡宸:老师们,同学们,早上好!我是来自四(4)中队的喻xx。昨天是西方的一个重要节日—复活节,今天由我来给大家分享一下复活节的由来和传统。复活节,也就是EasterDay,是一个非常重要的西方节日,在每年春分月圆之后的第一个星期日。今年是XX年4月16日,也就是昨天。基督徒认为,复活节象征重生与希望,是纪念耶稣基督于公元33年被钉死后第三天复活的事迹。
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。

人教A版高中数学必修一不同函数增长的差异教学设计(2)
本节课在已学幂函数、指数函数、对数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反应.而本节课重在研究不同函数增长的差异.课程目标1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.数学学科素养1.数学抽象:常见增长函数的定义、图象、性质;2.逻辑推理:三种函数的增长速度比较;3.数学运算:由函数图像求函数解析式;4.数据分析:由图象判断指数函数、对数函数和幂函数;5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结函数性质.重点:比较函数值得大小;难点:几种增长函数模型的应用.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。

人教A版高中数学必修一函数的表示法教学设计(2)
课本从引进函数概念开始就比较注重函数的不同表示方法:解析法,图象法,列表法.函数的不同表示方法能丰富对函数的认识,帮助理解抽象的函数概念.特别是在信息技术环境下,可以使函数在形与数两方面的结合得到更充分的表现,使学生通过函数的学习更好地体会数形结合这种重要的数学思想方法.因此,在研究函数时,要充分发挥图象的直观作用.在研究图象时,又要注意代数刻画以求思考和表述的精确性.课本将映射作为函数的一种推广,这与传统的处理方式有了逻辑顺序上的变化.这样处理,主要是想较好地衔接初中的学习,让学生将更多的精力集中理解函数的概念,同时,也体现了从特殊到一般的思维过程.课程目标1、明确函数的三种表示方法;2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;3、通过具体实例,了解简单的分段函数,并能简单应用.

人教A版高中数学必修一函数的应用(一)教学设计(2)
客观世界中的各种各样的运动变化现象均可表现为变量间的对应关系,这种关系常常可用函数模型来描述,并且通过研究函数模型就可以把我相应的运动变化规律.课程目标1、能够找出简单实际问题中的函数关系式,初步体会应用一次函数、二次函数、幂函数、分段函数模型解决实际问题; 2、感受运用函数概念建立模型的过程和方法,体会一次函数、二次函数、幂函数、分段函数模型在数学和其他学科中的重要性. 数学学科素养1.数学抽象:总结函数模型; 2.逻辑推理:找出简单实际问题中的函数关系式,根据题干信息写出分段函数; 3.数学运算:结合函数图象或其单调性来求最值. ; 4.数据分析:二次函数通过对称轴和定义域区间求最优问题; 5.数学建模:在具体问题情境中,运用数形结合思想,将自然语言用数学表达式表示出来。 重点:运用一次函数、二次函数、幂函数、分段函数模型的处理实际问题;难点:运用函数思想理解和处理现实生活和社会中的简单问题.

人教A版高中数学必修一集合的基本运算教学设计(2)
集合的基本运算是人教版普通高中课程标准实验教科书,数学必修1第一章第三节的内容. 在此之前,学生已学习了集合的含义以及集合与集合之间的基本关系,这为学习本节内容打下了基础. 本节内容是函数、方程、不等式的基础,在教材中起着承上启下的作用. 本节内容是高中数学的主要内容,也是高考的对象,在实践中应用广泛,是高中学生必须掌握的重点.课程目标1. 理解两个集合的并集与交集的含义,能求两个集合的并集与交集;2. 理解全集和补集的含义,能求给定集合的补集; 3. 能使用Venn图表达集合的基本关系与基本运算.数学学科素养1.数学抽象:并集、交集、全集、补集含义的理解;2.逻辑推理:并集、交集及补集的性质的推导;3.数学运算:求 两个集合的并集、交集及补集,已知并集、交集及补集的性质求参数(参数的范围);4.数据分析:通过并集、交集及补集的性质列不等式组,此过程中重点关注端点是否含“=”及?问题;
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.
人教A版高中数学必修二平面与平面平行教学设计
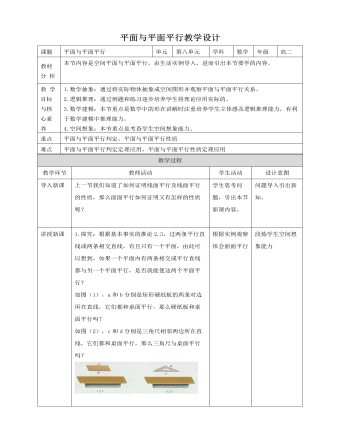
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
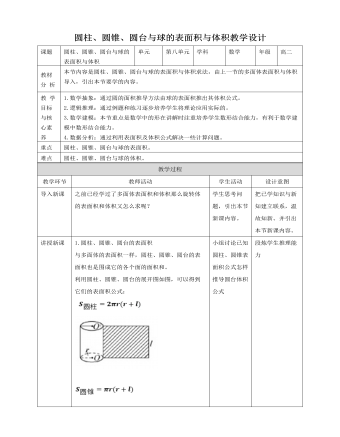
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.

