-

人教A版高中数学必修一函数y=Asin(ωχ+φ)教学设计(1)
本节课选自《普通高中课程标准实验教科书数学必修1》5.6.2节 函数y=Asin(ωx+φ)的图象通过图象变换,揭示参数φ、ω、A变化时对函数图象的形状和位置的影响。通过引导学生对函数y=sinx到y=Asin(ωx+φ)的图象变换规律的探索,让学生体会到由简单到复杂、由特殊到一般的化归思想;并通过对周期变换、相位变换先后顺序调整后,将影响图象变换这一难点的突破,让学生学会抓住问题的主要矛盾来解决问题的基本思想方法;通过对参数φ、ω、A的分类讨论,让学生深刻认识图象变换与函数解析式变换的内在联系。通过图象变换和“五点”作图法,正确找出函数y=sinx到y=Asin(ωx+φ)的图象变换规律,这也是本节课的重点所在。提高学生的推理能力。让学生感受数形结合及转化的思想方法。发展学生数学直观、数学抽象、逻辑推理、数学建模的核心素养。

人教A版高中数学必修一函数的表示法教学设计(2)
课本从引进函数概念开始就比较注重函数的不同表示方法:解析法,图象法,列表法.函数的不同表示方法能丰富对函数的认识,帮助理解抽象的函数概念.特别是在信息技术环境下,可以使函数在形与数两方面的结合得到更充分的表现,使学生通过函数的学习更好地体会数形结合这种重要的数学思想方法.因此,在研究函数时,要充分发挥图象的直观作用.在研究图象时,又要注意代数刻画以求思考和表述的精确性.课本将映射作为函数的一种推广,这与传统的处理方式有了逻辑顺序上的变化.这样处理,主要是想较好地衔接初中的学习,让学生将更多的精力集中理解函数的概念,同时,也体现了从特殊到一般的思维过程.课程目标1、明确函数的三种表示方法;2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;3、通过具体实例,了解简单的分段函数,并能简单应用.

人教A版高中数学必修一函数的零点与方程的解教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.5.1节《函数零点与方程的解》,由于学生已经学过一元二次方程与二次函数的关系,本节课的内容就是在此基础上的推广。从而建立一般的函数的零点概念,进一步理解零点判定定理及其应用。培养和发展学生数学直观、数学抽象、逻辑推理和数学建模的核心素养。1、了解函数(结合二次函数)零点的概念;2、理 解函数零点与方程的根以及函数图象与x轴交点的关系,掌握零点存在性定理的运用;3、在认识函数零点的过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学数形结合及函数思想; a.数学抽象:函数零点的概念;b.逻辑推理:零点判定定理;c.数学运算:运用零点判定定理确定零点范围;d.直观想象:运用图形判定零点;e.数学建模:运用函数的观点方程的根;

人教A版高中数学必修一集合的基本运算教学设计(2)
集合的基本运算是人教版普通高中课程标准实验教科书,数学必修1第一章第三节的内容. 在此之前,学生已学习了集合的含义以及集合与集合之间的基本关系,这为学习本节内容打下了基础. 本节内容是函数、方程、不等式的基础,在教材中起着承上启下的作用. 本节内容是高中数学的主要内容,也是高考的对象,在实践中应用广泛,是高中学生必须掌握的重点.课程目标1. 理解两个集合的并集与交集的含义,能求两个集合的并集与交集;2. 理解全集和补集的含义,能求给定集合的补集; 3. 能使用Venn图表达集合的基本关系与基本运算.数学学科素养1.数学抽象:并集、交集、全集、补集含义的理解;2.逻辑推理:并集、交集及补集的性质的推导;3.数学运算:求 两个集合的并集、交集及补集,已知并集、交集及补集的性质求参数(参数的范围);4.数据分析:通过并集、交集及补集的性质列不等式组,此过程中重点关注端点是否含“=”及?问题;

人教A版高中数学必修一简单的三角恒等变换教学设计(1)
四、小结1.知识:如何采用两角和或差的正余弦公式进行合角,借助三角函数的相关性质求值.其中三角函数最值问题是对三角函数的概念、图像和性质,以及诱导公式、同角三角函数基本关系、和(差)角公式的综合应用,也是函数思想的具体体现. 如何科学的把实际问题转化成数学问题,如何选择自变量建立数学关系式;求解三角函数在某一区间的最值问题.2.思想:本节课通过由特殊到一般方式把关系式 化成 的形式,可以很好地培养学生探究、归纳、类比的能力. 通过探究如何选择自变量建立数学关系式,可以很好地培养学生分析问题、解决问题的能力和应用意识,进一步培养学生的建模意识.五、作业1. 课时练 2. 预习下节课内容学生根据课堂学习,自主总结知识要点,及运用的思想方法。注意总结自己在学习中的易错点;

人教A版高中数学必修一简单的三角恒等变换教学设计(2)
它位于三角函数与数学变换的结合点上,能较好反应三角函数及变换之间的内在联系和相互转换,本节课内容的地位体现在它的基础性上。作用体现在它的工具性上。前面学生已经掌握了两角和与差的正弦、余弦、正切公式以及二倍角公式,并能通过这些公式进行求值、化简、证明,虽然学生已经具备了一定的推理、运算能力,但在数学的应用意识与应用能力方面尚需进一步培养.课程目标1.能用二倍角公式推导出半角公式,体会三角恒等变换的基本思想方法,以及进行简单的应用. 2.了解三角恒等变换的特点、变换技巧,掌握三角恒等变换的基本思想方法. 3.能利用三角恒等变换的技巧进行三角函数式的化简、求值以及证明,进而进行简单的应用. 数学学科素养1.逻辑推理: 三角恒等式的证明; 2.数据分析:三角函数式的化简; 3.数学运算:三角函数式的求值.
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教A版高中数学必修二直线与平面垂直教学设计
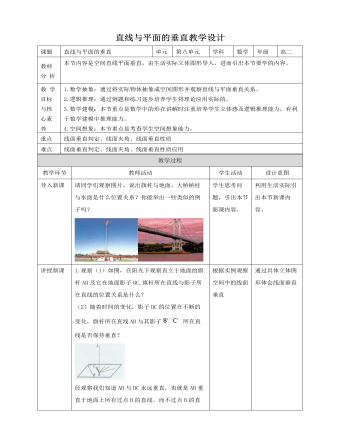
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.

农作物种子预约生产合同
根据《中华人民共和国经济合同法》、《中华人民共和国种子管理条例》及有关规定,为明确双方的权利义务,经双方协商一致,签订本合同。一、预约生产的农作物种子品种、质量、数量、金额: 农作物种类 品种名称 计量单位 数量 质量(%) 单价(元) 总金额(元)纯度 净度 发芽率 水份 合计人民币金额(大写): 万 仟 佰 拾 元 角 分二、预约方繁育材料: 材料品名 质量(%) 计量单位 数量 提供日期 亩用量 单价(元) 总金额(元)纯度 净度 发芽率 水份 合计人民币金额(大写): 万 仟 佰 拾 元 角 分三、农作物种子预约生产的环境及技术要求: 四、预约方提供技术服务的种类、方式及保密要求; 五、农作物种子质量检验及检疫严格按国家颁布的有关规定办理,检验执行GB/T3543.1~3543.7-1995《农作物种子检验规程》。 1.承约方必须持有《种子生产许可证》,交售种子时还须提供该批种子的有 效田间检验结果单、产地检疫合格证和《农作物种子质量合格证》。

技术转让和合作生产合同
第二章 合同内容及范围1.由乙方向甲方转让合同产品的设计、制造、销售、安装和维修使用的技术,合同产品的规格和技术参数详见本合同附件1。2.乙方负责向甲方提供合同产品全部有关技术和技术资料(以下简称资料),其具体内容和交付时间详见本合同附件2及附件3。3.乙方授与甲方在中国制造和销售合同产品的权利。前四台合同产品只在中国国内销售。在此以后甲方制造的合同产品可销往下列国家: ,如合同产品按政府间经济贸易协议规定销往其他国家或由中国承包商在中国购买,随承包工程出口,则不受上述规定的限制。4.在合同期间,如甲方需要,乙方有义务以优惠价格向甲方提供制造合同产品所需的部件及原材料,双方将通过协商另签合同。第一台及其后诸台合同产品的分工详见附件1。5.乙方负责图纸及资料的转化并在乙方工厂及其有关协作工厂培训甲方人员。乙方应尽最大努力使甲方人员掌握合同产品的技术(具体内容见本合同附件3)。6.乙方有义务派遣技术人员到甲方工厂进行技术服务(详见本合同附件4)。7.乙方同意向甲方提供所需的专用工具、夹具及设备和检测合同产品所需的技术资料(详见本合同附件2)。

LOGO、商标委托设计合同(范本)
根据《合同法》《著作权法》及相关法律、法规的规定,甲、乙双方在平等、自愿的基础之上,就甲方委托乙方设计公司LOGO和商标的相关事宜签订本合同,以资共同遵守。一、委托事项 甲方委托乙方设计公司的 LOGO和商标,乙方应提供不少于3套(含3套)设计方案供甲方选择。二、设计周期 设计周期分为二个阶段: 第一阶段: 个工作日(自本合同生效之日起算),完成设计初稿并提交甲方校稿。第二阶段: 个工作日(自甲方将修改意见反馈给乙方之日起算),完成设计修改并提交甲方验收。 若因乙方原因导致未能按上述约定期限交付的,每逾期一日乙方应按总设计费的万分之二向甲方支付违约金,甲方有权直接从设计费用里面直接扣除;逾期超过 个工作日,甲方有权单方终止本合同并要求乙方返还全部已收款项。

生产劳工劳动合同
甲方因生产经营需要,经考核,录用乙方(姓名)为(工程名称)工人,遵照国家有关劳动法律法规,经双方协商,签订本合同。第一条甲方录用乙方从事(工作名称)。第二条劳动合同期限从年月日起至年月日时止。其中试用期限为个月,至年月日止。第三条甲方的基本权利义务是:一、根据生产经营的需要和本单位的规章制度及本合同的各项条款对乙方进行管理。保护乙方的合法权益,按规定付给乙方工资、奖金、津贴以及保险福利和其他政策性补贴。

镇2022年工作总结及2023年工作思路
(一)推进产业优化升级,综合经济实力进一步增强。工业经济稳进提质。今年以来,国内外环境复杂性不确定性剧,我镇立足家电制造产业基础,因地制宜、准确识变、把握机遇,在不稳定不确定中积极谋求增长,把快制造业新旧动能转换、推动产业转型升级作为高质量发展的着力点,扎实推进全域产业治理。1-9月规上实现产值50.91亿元,同比增长2.43。三产动能持续释放。利用零土地招商引资、慈企回归、产销分离等综合手段、超常规工作力度,招商引资1家380万美元(外资),招商引资3家,分离发展1家。1-9月批发商品销售额增速26.7,限上商品销售额增速12.9,零售业商品销售额增速9.3,住宿餐饮业营业额增速20,社会消品零售总额增速17.3,限下社零增速11.2,商务经济领域各项数据全面由负转正,实现历史性突破。现代农业发展壮大。巩固“两非”整治成果,立足“溪上稻乡”项目,高效推进优质水稻生产基地、精品盆景花卉基地、农旅会客厅等个子项目建设,完成640亩早稻、300亩单季稻、500亩高粱的种植。启动面积740亩的四界村旱改水耕地质量提升项目。占地面积3130.86亩的高标准农田建设项目完成开招标投标并进场施工。 (二)推进城乡规划建设,城镇综合功能进一步完善。完善基础设施配套。推进国土空间规划编制,划定“三区三线”,进一步挖掘城镇存量用地,通过盘活存量,做优增量,促进镇社会经济健康发展。镇2022年度农村生活污水纳管治理工程(四界村二期)立项启动。完成镇中心小学光伏板1500平方的安装。建设停车位24只,解决群停车难问题。奋力攻坚重点工程。积极推进市重点项目慈溪市曹娥江引水工程慈溪中部通道基础设施配套工程(洋浦至蛟门浦)的房屋征收拆迁工作,截至11月2日,集体土地房屋拆迁签约率达到38.96。同时谋划启动三塘横江两侧生活休闲、商住宜居区域的规划布局。强势推进三改一拆。拆除违章建筑52起,占地面积78356平方米、建筑面积90359平方米,土地利用面积为81369平方米。处置下发的重点违法建筑13处,建筑面积达到56743平方米。完成农村乱占耕地建房专项整治,共发现、制止、查处违法案件108起,面积达16226.78平方米,下发责令停止违法行为通知书90份、责令限期整改违法行为通知书72份。

镇2022年度工作总结和2023年工作思路
一、主要工作开展情况 1、聚焦稳进提质,发展动能持续增强。一是狠抓平台建设。紧抓国土空间规划契机,强化镇工业东区、西区、北区及农业园区四个区产业发展空间优化拓展,稳步推进大河门山塘地块、榨菜整治提升产业园区、复线北侧地块四等相关工作,谋深谋实大河门山塘地块产业集聚区建设,完成采矿权拍卖亿元,着力拓展产业平台承载力。持续推进低效用地和园区二次开发利用,今年已盘活三和、世亚、华孚等处闲置厂房及用地,腾出空间约亩。二是狠抓项目建设。强力推进总投资亿元的容百锂电项目(目前容百-标段完成试生产,已进入投料试生产阶段),紧盯总投资亿元的松石、朗亿、柯仕等个在建项目,快复线北侧地块招商项目落地,截止月,我镇已完成宁波市外实到内资万元,市外实到内资万元,浙商创业创新实到资金完成元。大力推进“零土地”指标的增资扩产项目,切实提高土地容积率,提升亩均效益,目前瑞华、保世洁、珂仕二期等工业基建项目已基本完工。三是狠抓转型升级。深入开展稳链纾困助企活动,引导和鼓励企业练内功、拓市场、优布局,着力推动企业大技改投入,快企业智能化改造,完成企业高新企业培育入库家,高新申报家,宁波科技型中小企业备案家,国家科技型中小企业完成评价家。实现高新技术产业增值亿元,同比增长。四是狠抓特色农业。以味香园葡萄专业合作社为引领,充分打响打好“味香园”葡萄品牌,目前味香园葡萄品牌价值已达亿元人民币。持续深化农旅融合,以“()江南葡萄节”为活动载体,积极拓展“直播带货”、“夜市经济”等销售推广渠道,全年葡萄采摘游客达到万人次以上,经济效益超亿元。 2、聚焦全域提升,城乡品质持续优化。一是城镇品质巩固提升。深入开展“精特亮”创建,总投资万元“果香姚北”乡村明线段顺利完工。全力开展“拆违治乱”百日攻坚行动,处置违章宗,拆除面积万平方米,并以“白+黑”、“5+2”之势攻坚完成国土变调查问题销整改近亩。集中力量推进N连接线土地征用及房屋拆迁工作,实现房屋拆迁“清零”,完成征地签约率。持续推进老街立面改造及历史风貌建筑修缮,今年共完成户民居仿古改造,投入资金约万元。二是美丽乡村优化升级。以邵家丘村“未来乡村”建设为引领,深入开展兰海、临海、临浦等个村“精特亮”创建工程及村新时代美丽乡村梳理式改造,抓牢全域土地整治“一村一策”主攻方向,截止目前已为村级集体经济减少债务余万元。着力深化“一扫七治”、明村镇创建整改、垃圾分类等工作,深入开展农村环境“大清理、大起底”综合整治百日攻坚行动,逗硬整治人居环境突出问题。三是生态环境持续改善。快镇域范围内污水管网建设,省级“污水零直排区”创建、工业西区“污水零直排区”创建通过验收,北区省创、东区县创快推进。持续深化“五水共治”,重点实施大浦江水质提升工程,做好大浦江宁波生态补偿考核断面Ⅲ类水质达标及七塘横江段“甬有碧水”考核任务。成功创建国家卫生镇,探索实施全域保洁一体化。推进投资万元的生活垃圾填埋场处置项目,预计月底全部完工,年底前销。

乡2023年工作总结和2024年工作思路
三、2024年工作思路(一)深耕不辍服务保障。紧紧围绕偏远山区“一老一少”现实需求,持续深化“共富食堂”品牌,继续盘活社会慈善力量,壮大基本兜底资金盘。延伸服务范围,探索偏远自然村“邻里和睦互助点”的运行,持续推进留守学生“营养餐”工程,真正将“一老一少”的需求解决在实际问题上。(二)高质发展农业产业。利用本乡17.4万亩的山场优势,盘活乡林场资源,在现有的高山红薯、油茶、谷精草等基地基础上提质扩面,真正形成相对完善的产业链条,打造“XX红”系列农业品牌,实现群众在家门口增收;(三)全力推进环境治理。抓好环境治理和生态保护,全面推进全域环境综合整治,提升人居环境。秉承“一村一品”建设目标,推进环境整治,狠抓生态保护工作,探索森林消防长效机制,确保楠溪江源头生态绝对安全。以溪界公路生态景观带打造、建成区风貌整治工程等改造行动为抓手,项目化推进宜居、宜业、宜游的美丽乡村建设,助推“浙”里乡村奔向共富共美“嘉”生活。

2023年工作总结和2024年工作思路
加强区域餐饮食品安全基础保障能力体制机制建设,针对疫情期间餐饮保供所暴露出的应急机制缺失、协同处置缺位等问题,将各基础能力要素集成进行数字赋能,探索打造全新全域餐饮食品安全保供系统应用,构建“组织机制协调顺畅”、“法定职责责任明确”、“制度流程设计清晰”、“部门监管协同高效”、“食品安全保供精准”、“专业技术支撑有力”等六大功能模块,切实加强平时“专业化监管、跨部门协作、社会化共治”等三大能力建设,确保重大活动保障、突发公共事件,餐饮保供随时能“拉得出、打得赢”。持续推进星级农村食品经营示范店建设,完善并推广农村食品监管数字化模型,力争在农村食品安全监管上精准破题。全面推进两个“规定”落实,建立两证和强标类工业产品生产和销售单位质量安全档案,督促企业健全质量管理相关制度。发挥部门优势,做好新开工大型项目的特种设备服务工作,变“事后监督”为“事前服务”,为企业建设及后续安全使用管理打下坚实基础。



