-

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示

北师大初中九年级数学下册弧长及扇形的面积教案
1.了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用;(重点)2.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长l=nπR180和扇形面积S扇=nπR2360的计算公式,并应用这些公式解决一些问题.(难点)一、情境导入如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14,所以铁轨的长度l≈2×3.14×1004=157(米). 如果圆心角是任意的角度,如何计算它所对的弧长呢?二、合作探究探究点一:弧长公式【类型一】 求弧长如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()
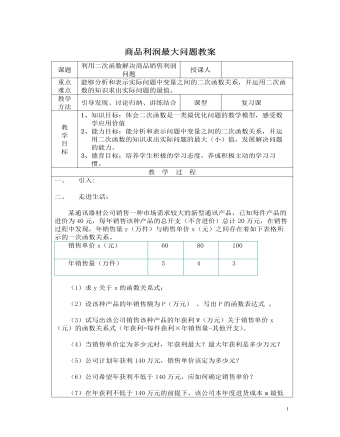
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。

北师大初中九年级数学下册三角函数的应用1教案
然后,她沿着坡度是i=1∶1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度(参考数据:2≈1.41,结果精确到0.1米).解析:作辅助线EF⊥AC于点F,根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,通过平角减去其他角从而得到∠AEF=45°,即可求出AE的长度.解:作EF⊥AC于点F,根据题意,得CE=18×15=270(米). ∵tan∠CED=1,∴∠CED=∠DCE=45°.∵∠ECF=90°-45°-15°=30°,∴EF=12CE=135米.∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°-45°-60°-30°=45°,∴AE=2EF=1352≈190.4(米).所以,娱乐场地所在山坡AE的长度约为190.4米.方法总结:解决本题的关键是能借助仰角、俯角和坡度构造直角三角形,并结合图形利用三角函数解直角三角形.

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册圆内接正多边形教案
解析:正多边形的边心距、半径、边长的一半正好构成直角三角形,根据勾股定理就可以求解.解:(1)设正三角形ABC的中心为O,BC切⊙O于点D,连接OB、OD,则OD⊥BC,BD=DC=a.则S圆环=π·OB2-π·OD2=πOB2-OD2=π·BD2=πa2;(2)只需测出弦BC(或AC,AB)的长;(3)结果一样,即S圆环=πa2;(4)S圆环=πa2.方法总结:正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径、外接圆半径、边心距,中心角之间的计算转化为解直角三角形.变式训练:见《学练优》本课时练习“课后巩固提升”第4题【类型四】 圆内接正多边形的实际运用如图①,有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心(下列各题结果精确到0.1m).(1)求地基的中心到边缘的距离;(2)已知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?

XX中学2023—2024学年度第一学期小学部教学工作计划
8、加强对音、体、美、等课程实施的监督与检查,确保上足课节。9、将学困生转化工作及优生培养工作落到实处。提高对学困生的关注度,加强对学困生的心理辅导及课业辅导。10、每周一次级部长会,每月一次学科长会,建立教务会议记录,学科教研、活动记录,教师上交材料记录。11、本学期共21周,实际授课17周。五、教学工作配档表九月1、划分班级,安排好教师课务,排好课程表。2、参加XX市教研室召开的小学教学教研工作会议3、安排各科教师参加XX市教研室组织的学科研讨。4、制定好各种教学、教研工作计划。5、安排并开展本学期公开课活动。6、印发各种表册。7、对小一新生建档。8、做好十一长假的作业布置工作十月1、组织学习烟台市小学教学常规、课程标准的学习。2、检查集体备课情况。3、进行书法、口算、口语表达技能比赛。4、积极准备上级的专项教学常规督导。5、积极打磨XX市学科优质课。

离婚协议书(子女已成年)
三、女儿/儿子_________的医药费,在_________元以内由抚养方先垫付,凭票甲、乙双方各承担一半,超过_________元,由抚养方通知未抚养方,双方共同承担。

疫情防控应急预案(镇乡)
(二)工作原则1.加强预防。增强忧患意识,高度重视公共安全工作,坚持预防与应急相结合,常态与非常态相结合,做好应对新型冠状病毒感染者的思想准备、预案准备、组织准备以及物资准备等。2.快速反应。新型冠状病毒感染事件应急处置的各环节都要坚持效率原则,建立健全快速反应机制,及时获取充分而准确的信息,跟踪研判,果断决策,迅速处置,最大程度地减少危害和影响。

(冬季安全)的国旗下讲话
真正的寒冬开始了,大家穿戴都比较严实,遮挡了视线,手脚也不够灵活了。在这样的情况下,万一出现意外比较难以应对。在此,我和大家讲讲学校冬季安全小知识。一、行路安全由于早晨大雾茫茫,或者冰冻,影响了汽车的刹车性能。因此,步行外出时要注意,一定要靠路边行走。横过马路时,要注意来往车辆,不要斜穿、猛跑;在通过十字路口时,不得横过马路。冬天更不要在结有薄冰的湖面、河面、小溪边玩耍,这样最容易出事。二、运动安全冬季长跑是一项不错的体育运动,但是在长跑锻炼前准备活动一定要充分,并系好鞋带。锻炼后还要做整理活动,同时一定要注意保暖,以防感冒。我们还需要特别注意,在集体长跑中,不可以推推搡搡,或者手插在口袋里,或者一边跑步一边讲话,这样很容易发生意外,也不利于健康。

(春季开学)国旗下讲话
经过了一个愉快的寒假,我们满怀着新的希望迎来了生机勃勃的XX年春季,同学们春季是播种的季节,只有用辛勤的劳动播下希望的种子,到时候才会有满意的收获。俗话说:“栽什么树苗结什么果,撒什么种子开什么花。”那么请问亲爱的同学,在这个春季里,你打算播下什么样的种子呢?为了能让我们梦想成真,让我们在新的学期里发扬互帮互助、积极主动、探索创新、努力进取的精神,取得各自满意的成绩。下面,我代表全体老师向同学们提出如下几点要求:一、自我调整,按时到校新学期的开始,意味着紧张的学习已经来临,各位同学要开展自我调整,并把以休息为主的假期生活,调整到以学习为主的校园生活中来,要把全部精力投入到学习上来;要调整作息时间,晚上要按时睡觉,保证第二天有充沛精力投入学习。做到按时到校,服从学校以及老师的部署。

(国庆节)国旗下讲话:爱国
今天我非常荣幸,能够站在庄严的国旗下为大家讲话。再过几天就是国庆节了,这不禁使我想起那些为了新中国的成立而抛头颅、洒热血、无私奉献的英雄们!回顾我们中华民族的历史长河,有无数的爱国志士至今还活在我们心中:有岳飞、郑成功、孙中山 李大钊等等。新中国成立以后,更是有许多杰出人物,如邓稼先、华罗庚、钱学森等等。这些人的光辉形象和他们的历史贡献,永远激励着我们每一个中国人。提起“爱国”这个词,那可是一个神圣的字眼。爱国是什么?爱国是热爱祖国的山河,热爱民族的历史,关心祖国的命运,体恤人民的疾苦,在危难时刻英勇战斗,为祖国捐躯的英雄壮举等等。

(九一八事变)国旗下讲话
今天是20XX年9月15日,再过三天是9月18日,83年前的这一天这是一个令所有中国人都不能忘怀的日子。1931年9月18日,日本关东军经过精心策划,炸毁了南满铁路柳条湖段,布置假现场,污蔑中国军队破坏,并以此为借口,炮轰我东北军大营,随后攻占沈阳,制造了震惊中外的“九·一八"事变”。而九·一八"事变爆发后不到半年,东北三省全部落入日军之手。时隔80多年后的今天,旧时的伤痛早在时间的冲刷下被磨灭殆尽,可是我们并不能忘记那些不堪回首的记忆。不能将我们民族曾经的屈辱和血泪遗忘。即使我们不曾经历,心底也应深深印刻着八个字:正视历史,勿忘国耻!要如何正视历史?我们要有一个正确的态度。日本至今仍存在军国主义,想要侵占我钓鱼岛主权;日本当局还试图篡改历史教科书,掩盖曾经的罪行。这些我们当然要抗议,要反对。但也要想清楚我们反对的对象是什么?人生而平等,没有人是天生残暴无良的。是战争使得人性丧失,导致一个个悲剧的发生。古今中外这样的例子层出不穷,所以我们要反对的是引发欲望和杀戮的战争。我想,不仅是日本,那些曾对中国犯下侵略罪行的许多国家,都应该对历史进行反思。爱国之情固然高尚,但也要以理性的形式来表达。虽抱有一个良好的目的,如果不采取恰当合理的方式,很有可能造成不好的结果。口号响亮最多表明你精力充沛,并不表示你的立场正确;正义不会因为你游行、砸日本车而站在你这边,非理性的行为非但不能达到目的,只会给自己的同胞添堵。

(九月)新学期国旗下讲话
上学期,在辅导老师和许多同学的共同努力下,学校取得了多项荣誉,获得了XX市三会活动先进学校称号,六(1)班被评为XX区书香班级,四(2)班整班钢笔字比赛获XX区一等奖。同时,个人奖也取得了不少。有30位同学获XX市阅读之星、XX区三好学生、学科十佳等荣誉称号。有100多名同学在书法、美术、作文、科学论文、诗歌朗诵、舞蹈、体育、乐器演奏等各项各级竞赛中获奖。有近20名同学撰写的文章发表在《苏州日报》、《百家作文指导》等刊物上。转眼间,两个月的暑期生活已经结束。在这个假期中,有的同学在爸爸妈妈带领下,外出旅游观光,开阔了自己的眼界;有的同学广泛阅读课外书,丰富自己的知识;还有的同学积极参加公益活动、家务劳动,提高自己的动手能力;很多同学参加了各种兴趣小组的活动,增长了不少知识和本领;学校田径队的同学更是冒着炎热坚持训练,像许苏磊、肖淑瑶、施誉雯、侯沁鹏等同学训练刻苦,成绩提高很快;开学前,五年级部分学生参加语文、数学三会活动集训,争取在竞赛中取得好成绩……大家都度过了一个丰富多彩、有声有色,颇有收获的暑假。

(元旦)国旗下讲话:《迎新年》
元旦,也被称为“新年”或“新历年”,是指公历的1月1日。但在古代,“元旦”即是今天的“春节”,也就是农历新年。元旦是很多国家的法定假日;在中国大陆、台湾、香港和澳门,元旦均为法定假日;中国大陆及台湾均作为法定假日休假一天。习俗方面,“元旦”主要以各种方式互相祝福,贺年卡是其中主要形式。汉语“元旦”涵义:“元”是开始、第一的意思;“旦”即早晨天明的时间,也通常包含一天之意。因此“元旦”就是一年的开始、一年的第一天。民国以前,元旦即现在的春节。历史上,中国各个朝代对“元旦”说法不一致夏代为正月初一(夏历1月1日)商代为十二月初一(12月1日)周代为十一月初一(11月1日)秦王朝时期为十月初一(10月1日)
