-

日益重要的国际组织 说课稿
一、说教材(一)教材分析本课是最新部编版《道德与法治》六年级下册第四单元第9 课。本课首先 明确了国际组织的定义,并介绍了两种国际组织的划分标准。接着为学生呈现 了国际奥林匹克委员会、东南亚国家联盟、世界银行、世界卫生组织这四个国 际组织的标志以及职责。课文通过图文并茂的形式让学生通过画面与文字感性 地了解国际组织在国际事务中起着重要的作用。(二)教学目标1. 了解什么是国际组织、国际组织的分类及重要作用,培养开放的国际视野。2. 了解联合国和世界贸易组织,知道这两个国际组织在国际政治、经济中 发展的重要作用,明白中国与国际组织的交流、推动作用。3. 初步掌握收集、整理和运用信息的能力。(三)教学重难点 教学重点:知道国际组织的分类及重要作用,了解联合国和世界贸易组织的构成和作用,明白中国与国际组织的相互交流、支持作用。 教学难点:国际组织的分类及重要作用。 二、说学情分析:从学生的学习角度上分析,在知识层面上,六年级的学生对国际组织以及 不同国际组织所处理的一些国际性事务方面的内容比较陌生,也比较遥远。相对来说,它知识性较强,趣味性不足,因此教师要努力挖掘课本知识和拓展资料,激发学生的学习兴趣,比如:布置课前预习,让学生通过网络或书籍收集 不同国际组织的资料,对国际组织有一个初步的印象;课堂学习时,抓住学生 互动学习、交流的时间,了解不同国际组织的职责以及在国际事务中发挥的巨 大作用。

大班社会教案:兔奶奶的生日会
一、 阅读来信和礼物券 1、(出示信封)今天早上,妈妈在信箱里发现了一封信,猜猜是谁写给我们的? 2、猜谜语:红眼睛,白皮袄/长耳朵,真灵巧/爱吃萝卜和青菜/走起路来跳呀跳 3、哟,是写给我们的呀!咦,会是谁给我们写的信呢? 4、引导幼儿观察信封右下角的兔奶奶:(老花眼镜、额头的皱纹等) 5、兔奶奶写信给我们,不知道有什么事,让我们一起看看,好吗? 6、师生一起读信(教师读信,引导幼儿看图) a、(蛋糕)这是什么呀?什么时候要吃蛋糕? B、原来,兔奶奶要生日了,她请我们去干什么?那你们谁想去?

我们所了解的环境污染 说课稿
本节课我设计了导入新课、学习新知、课堂小结、布置作业四个教学环节。环节一:创设情境,导入新课教师用多媒体播放塑料制品给人们的生活带来危害的两则新闻报道:一则是废弃的塑料制品留在土壤中影响庄稼的生长, 一则是塑料袋被鱼类误食,导致鱼的死亡。学生说说看了之后有什么感受?会想到哪些问题?教师引导到有关“白色污染”的话题,由此导入新课,板书课题:我们所了解的环境污染。设计意图:激发学生的学习兴趣,引出本节课要学习的内容,为接下来的学习作好铺垫。环节二:合作探究,学习新课这一环节我安排了三个活动。活动一:关于塑料制品学生先说说在日常生活中见过哪些塑料制品,教师再引导学生一起探究塑料有哪些性能,然后,学生说说有什么感受?设计意图:引导学生客观地认识塑料制品,感受塑料制品给人们的生活带来了很多便利。活动二:“白色污染”的成因与危害学生阅读教材第73页的知识窗阅读角,结合课前调查、收集到的有关“白色污染”的有关资料,先在小组内交流:“白色污染”是怎样形成的?这些塑料垃圾给人们带来了哪些困扰?说说了解之后有什么感受?再全班汇报交流,教师相机引导。板书:塑料袋和塑料制品,破坏市容环境,危害人体健康,危及动物安全,污染大气环境,影响农业生产,破坏臭氧层等。

精编学校开展拓展训练心得体会与收获参考范文
拓展训练一下子使我对前途的挑战欲望猛然增强。在工作中,业务的拓展往往无法预见其结果,使自己裹足不前。但拓展训练使自己猛然醒悟到在今后的工作中,不要因为不可认知而畏惧,不要因从来未尝试过而轻言放弃。一个人对自身的认识往往是有保留的,对自己的潜能认识是模糊的、低估的。拓展训练使自己更清晰地认识到自己身上潜伏的能量,增强了自己克服困难,迎接挑战的信心与决心。通过拓展训练,我重新认识到了自身的潜能,也将把这种潜力发挥到以后的工作中。

关于参与红色教育社会实践活动心得体会八篇
一段岁月,波澜壮阔,刻骨铭心。一种精神,穿越历史,辉映未来。感谢我行领导给我们的这次参观学习的机会,让我们更加深刻的领会到新中国的诞生源之于无数仁人志士坚持自己的理想,信仰,抛头颅,洒热血,前仆后继,英勇战斗而换来的人民当家作主的政权。 我们从中获取了很多人生启迪,吸取了宝贵的精神营养,我们要学习老一辈无产阶级革命家,将革命先驱崇高革命精神的落实到实处,贯穿在工作当中。铭记历史,牢固树立新时期的革命精神,全心全意立足本职岗位,脚踏实地,努力工作,无私奉献,以更大的热情投入到工作中去,为社会的和谐与进步贡献自己的力量。

精编学生参加家务劳动心得体会与收获参考范文
学生素质教育,加强和改进青年学生思想政治工作,引导学生健康成长成才的重要举措,作为培养和提高学生实践、创新和创业能力的重要途径,一直来深受学校的高度重视。社会实践活动一直被视为高校培养德、智、体、美、劳全面发展的跨世纪优秀人才的重要途径。寒假期间社会实践活动是学校教育向课堂外的一种延伸,也是推进素质教育进程的重要手段。它有助于当代大学生接触社会,了解社会。同时,实践也是大学生学习知识、锻炼才干的有效途径,更是大学生服务社会、回报社会的一种良好形式。多年来,社会实践活动已在我校蔚然成风。
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点

【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 我们知道,在直角三角形(如图)中,,,即 ,, 由于,所以,于是 . 图1-6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中,是否也存在类似的数量关系呢? c 图1-7 当三角形为钝角三角形时,不妨设角为钝角,如图所示,以为原点,以射线的方向为轴正方向,建立直角坐标系,则 两边取与单位向量的数量积,得 由于设与角A,B,C相对应的边长分别为a,b,c,故 即 所以 同理可得 即 当三角形为锐角三角形时,同样可以得到这个结论.于是得到正弦定理: 在三角形中,各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题: (1)已知三角形的两个角和任意一边,求其他两边和一角. (2)已知三角形的两边和其中一边所对角,求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.1《排列与组合》优秀教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 3.1 排列与组合. *创设情境 兴趣导入 基础模块中,曾经学习了两个计数原理.大家知道: (1)如果完成一件事,有N类方式.第一类方式有k1种方法,第二类方式有k2种方法,……,第n类方式有kn种方法,那么完成这件事的方法共有 = + +…+(种). (3.1) (2)如果完成一件事,需要分成N个步骤.完成第1个步骤有k1种方法,完成第2个步骤有k2种方法,……,完成第n个步骤有kn种方法,并且只有这n个步骤都完成后,这件事才能完成,那么完成这件事的方法共有 = · ·…·(种). (3.2) 下面看一个问题: 在北京、重庆、上海3个民航站之间的直达航线,需要准备多少种不同的机票? 这个问题就是从北京、重庆、上海3个民航站中,每次取出2个站,按照起点在前,终点在后的顺序排列,求不同的排列方法的总数. 首先确定机票的起点,从3个民航站中任意选取1个,有3种不同的方法;然后确定机票的终点,从剩余的2个民航站中任意选取1个,有2种不同的方法.根据分步计数原理,共有3×2=6种不同的方法,即需要准备6种不同的飞机票: 北京→重庆,北京→上海,重庆→北京,重庆→上海,上海→北京,上海→重庆. 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 15*动脑思考 探索新知 我们将被取的对象(如上面问题中的民航站)叫做元素,上面的问题就是:从3个不同元素中,任取2个,按照一定的顺序排成一列,可以得到多少种不同的排列. 一般地,从n个不同元素中,任取m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,时叫做选排列,时叫做全排列. 总结 归纳 分析 关键 词语 思考 理解 记忆 引导学生发现解决问题方法 20
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?

人教A版高中数学必修一单调性与最大(小)值教学设计(1)
《函数的单调性与最大(小)值}》系人教A版高中数学必修第一册第三章第二节的内容,本节包括函数的单调性的定义与判断及其证明、函数最大(小)值的求法。在初中学习函数时,借助图像的直观性研究了一些函数的增减性,这节内容是初中有关内容的深化、延伸和提高函数的单调性是函数众多性质中的重要性质之一,函数的单调性一节中的知识是前一节内容函数的概念和图像知识的延续,它和后面的函数奇偶性,合称为函数的简单性质,是今后研究指数函数、对数函数、幂函数及其他函数单调性的理论基础;在解决函数值域、定义域、不等式、比较两数大小等具体问需用到函数的单调性;同时在这一节中利用函数图象来研究函数性质的救开结合思想将贯穿于我们整个高中数学教学。

人教A版高中数学必修一充分条件与必要条件教学设计(2)
【例3】本例中“p是q的充分不必要条件”改为“p是q的必要不充分条件”,其他条件不变,试求m的取值范围.【答案】见解析【解析】由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0(m>0)得1-m≤x≤1+m(m>0)因为p是q的必要不充分条件,所以q?p,且p?/q.则{x|1-m≤x≤1+m,m>0}?{x|-2≤x≤10}所以m>01-m≥-21+m≤10,解得0<m≤3.即m的取值范围是(0,3].解题技巧:(利用充分、必要、充分必要条件的关系求参数范围)(1)化简p、q两命题,(2)根据p与q的关系(充分、必要、充要条件)转化为集合间的关系,(3)利用集合间的关系建立不等关系,(4)求解参数范围.跟踪训练三3.已知P={x|a-4<x<a+4},Q={x|1<x<3},“x∈P”是“x∈Q”的必要条件,求实数a的取值范围.【答案】见解析【解析】因为“x∈P”是x∈Q的必要条件,所以Q?P.所以a-4≤1a+4≥3解得-1≤a≤5即a的取值范围是[-1,5].五、课堂小结让学生总结本节课所学主要知识及解题技巧

人教A版高中数学必修一充分条件与必要条件教学设计(1)
本课是高中数学第一章第4节,充要条件是中学数学中最重要的数学概念之一, 它主要讨论了命题的条件与结论之间的逻辑关系,目的是为今后的数学学习特别是数学推理的学习打下基础。从学生学习的角度看,与旧教材相比,教学时间的前置,造成学生在学习充要条件这一概念时的知识储备不够丰富,逻辑思维能力的训练不够充分,这也为教师的教学带来一定的困难.“充要条件”这一节介绍了充分条件,必要条件和充要条件三个概念,由于这些概念比较抽象,中学生不易理解,用它们去解决具体问题则更为困难,因此”充要条件”的教学成为中学数学的难点之一,而必要条件的定义又是本节内容的难点.A.正确理解充分不必要条件、必要不充分条件、充要条件的概念;B.会判断命题的充分条件、必要条件、充要条件.C.通过学习,使学生明白对条件的判定应该归结为判断命题的真假.D.在观察和思考中,在解题和证明题中,培养学生思维能力的严密性品质.

人教A版高中数学必修一单调性与最大(小)值教学设计(2)
《函数的单调性与最大(小)值》是高中数学新教材第一册第三章第2节的内容。在此之前,学生已学习了函数的概念、定义域、值域及表示法,这为过渡到本节的学习起着铺垫作用。学生在初中已经学习了一次函数、二次函数、反比例函数的图象,在此基础上学生对增减性有一个初步的感性认识,所以本节课是学生数学思想的一次重要提高。函数单调性是函数概念的延续和拓展,又是后续研究指数函数、对数函数等内容的基础,对进一步研究闭区间上的连续函数最大值和最小值的求法和实际应用,对解决各种数学问题有着广泛作用。课程目标1、理解增函数、减函数 的概念及函数单调性的定义;2、会根据单调定义证明函数单调性;3、理解函数的最大(小)值及其几何意义;4、学会运用函数图象理解和研究函数的性质.数学学科素养

人教A版高中数学必修一等式性质与不等式性质教学设计(2)
等式性质与不等式性质是高中数学的主要内容之一,在高中数学中占有重要地位,它是刻画现实世界中量与量之间关系的有效数学模型,在现实生活中有着广泛的应,有着重要的实际意义.同时等式性质与不等式性质也为学生以后顺利学习基本不等式起到重要的铺垫.课程目标1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题.2. 进一步掌握作差、作商、综合法等比较法比较实数的大小. 3. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质。数学学科素养1.数学抽象:不等式的基本性质;2.逻辑推理:不等式的证明;3.数学运算:比较多项式的大小及重要不等式的应用;4.数据分析:多项式的取值范围,许将单项式的范围之一求出,然后相加或相乘.(将减法转化为加法,将除法转化为乘法);5.数学建模:运用类比的思想有等式的基本性质猜测不等式的基本性质。

人教A版高中数学必修一全称量词与存在量词教学设计(2)
(4)“不论m取何实数,方程x2+2x-m=0都有实数根”是全称量词命题,其否定为“存在实数m0,使得方程x2+2x-m0=0没有实数根”,它是真命题.解题技巧:(含有一个量词的命题的否定方法)(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称量词命题还是存在量词命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.跟踪训练三3.写出下列命题的否定,并判断其真假:(1)p:?x∈R,x2-x+ ≥0;(2)q:所有的正方形都是矩形;(3)r:?x∈R,x2+3x+7≤0;(4)s:至少有一个实数x,使x3+1=0.【答案】见解析【解析】(1) p:?x∈R,x2-x+1/4<0.∵?x∈R,x2-x+1/4=(x"-" 1/2)^2≥0恒成立,∴ p是假命题.
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
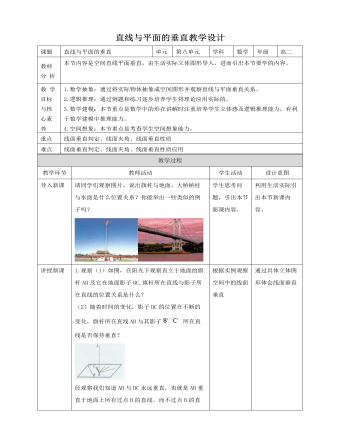
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.