-

北师大初中九年级数学下册弧长及扇形的面积教案
1.了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用;(重点)2.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长l=nπR180和扇形面积S扇=nπR2360的计算公式,并应用这些公式解决一些问题.(难点)一、情境导入如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14,所以铁轨的长度l≈2×3.14×1004=157(米). 如果圆心角是任意的角度,如何计算它所对的弧长呢?二、合作探究探究点一:弧长公式【类型一】 求弧长如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()
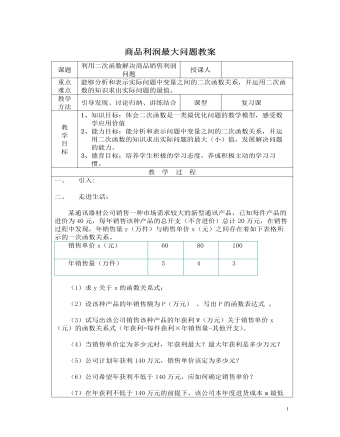
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册切线的判定及三角形的内切圆教案
解析:(1)连接BI,根据I是△ABC的内心,得出∠1=∠2,∠3=∠4,再根据∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,得出∠BIE=∠IBE,即可证出IE=BE;(2)由三角形的内心,得到角平分线,根据等腰三角形的性质得到边相等,由等量代换得到四条边都相等,推出四边形是菱形.解:(1)BE=IE.理由如下:如图①,连接BI,∵I是△ABC的内心,∴∠1=∠2,∠3=∠4.∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,∴∠BIE=∠IBE,∴BE=IE;(2)四边形BECI是菱形.证明如下:∵∠BED=∠CED=60°,∴∠ABC=∠ACB=60°,∴BE=CE.∵I是△ABC的内心,∴∠4=12∠ABC=30°,∠ICD=12∠ACB=30°,∴∠4=∠ICD,∴BI=IC.由(1)证得IE=BE,∴BE=CE=BI=IC,∴四边形BECI是菱形.方法总结:解决本题要掌握三角形的内心的性质,以及圆周角定理.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

北师大初中九年级数学下册圆内接正多边形教案
解析:正多边形的边心距、半径、边长的一半正好构成直角三角形,根据勾股定理就可以求解.解:(1)设正三角形ABC的中心为O,BC切⊙O于点D,连接OB、OD,则OD⊥BC,BD=DC=a.则S圆环=π·OB2-π·OD2=πOB2-OD2=π·BD2=πa2;(2)只需测出弦BC(或AC,AB)的长;(3)结果一样,即S圆环=πa2;(4)S圆环=πa2.方法总结:正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径、外接圆半径、边心距,中心角之间的计算转化为解直角三角形.变式训练:见《学练优》本课时练习“课后巩固提升”第4题【类型四】 圆内接正多边形的实际运用如图①,有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心(下列各题结果精确到0.1m).(1)求地基的中心到边缘的距离;(2)已知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?

北师大初中九年级数学下册圆周角和圆心角的关系教案
解析:点E是BC︵的中点,根据圆周角定理的推论可得∠BAE=∠CBE,可证得△BDE∽△ABE,然后由相似三角形的对应边成比例得结论.证明:∵点E是BC︵的中点,即BE︵=CE︵,∴∠BAE=∠CBE.∵∠E=∠E(公共角),∴△BDE∽△ABE,∴BE∶AE=DE∶BE,∴BE2=AE·DE.方法总结:圆周角定理的推论是和角有关系的定理,所以在圆中,解决相似三角形的问题常常考虑此定理.三、板书设计圆周角和圆心角的关系1.圆周角的概念2.圆周角定理3.圆周角定理的推论本节课的重点是圆周角与圆心角的关系,难点是应用所学知识灵活解题.在本节课的教学中,学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握,理解起来问题也不大,而对圆周角与圆心角的关系理解起来则相对困难,因此在教学过程中要着重引导学生对这一知识的探索与理解.还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题,在教学过程中要对此予以足够的强调,借助多媒体加以突出.

北师大初中九年级数学下册直线和圆的位置关系及切线的性质教案
解析:(1)由切线的性质得AB⊥BF,因为CD⊥AB,所以CD∥BF,由平行线的性质得∠ADC=∠F,由圆周角定理的推论得∠ABC=∠ADC,于是证得∠ABC=∠F;(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,然后运用解直角三角形解答.(1)证明:∵BF为⊙O的切线,∴AB⊥BF.∵CD⊥AB,∴∠ABF=∠AHD=90°,∴CD∥BF.∴∠ADC=∠F.又∵∠ABC=∠ADC,∴∠ABC=∠F;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°.由(1)可知∠ABF=90°,∴∠ABD+∠DBF=90°,∴∠A=∠DBF.又∵∠A=∠C,∴∠C=∠DBF.在Rt△DBF中,sin∠DBF=sinC=35,DF=6,∴BF=10,∴BD=8.在Rt△ABD中,sinA=sinC=35,BD=8,∴AB=403.∴⊙O的半径为203.方法总结:运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

部编版语文八年级下册《马说》教案
课时分配 建议本课依据学情分课时。第一课时进行自主学习反馈及文意梳理、整体感知。第二课时进行课文具体分析的交流展示及当堂检测。可适当调节。教学目标 知识与技能 1.掌握文章中的一些重点词语的含义,积累一些文言知识。2.结合课后注释,疏通文章意思,逐步提高文言文的朗读和疏通能力。过程与方法 1.通过不同形式的朗读,理解短文所阐明的深刻道理。2.通过合作探究的学习方式,引导学生体会文章语言的精妙。情感、态度与价值观 注重对学生的情感熏陶,让学生认识封建统治者不识人才、埋没人才的昏庸,引导学生认识到在今天的优越条件下,要努力使自己成为有用之才。

小说红与黑读书心得参考范本
司汤达是善于从爱情中反映重大社会问题的文学大师。于连的两次爱情都与时代风云紧密相连,这是当时阶级角逐的一种表现形式,他对德·雷纳尔夫人后来的确也产生了真正的感情,但开始是出于小市民对权贵的报复心理。因此,于连第一次占有德·雷纳尔夫人的手的时候,他感到的并不是爱情的幸福,而是拿破仑式的野心的胜利,是"狂欢"和"喜悦",是报复心理的满足。 如果说于连对德·雷纳尔夫人的追求还有某些真挚情感的话,那么于连对玛蒂尔德小姐的爱情则纯属政治上的角逐,玛蒂尔德既有贵族少女的傲慢,任性的气质,又受到法国_的深刻影响。她认为,如果再有一次_,主宰社会的必定是像于连这样富于朝气的平民青年。同于连结成伉俪,既富于浪漫气息,又找到了有力的靠山。而于连则认为与玛蒂尔德小姐结婚可以爬上高位,青云直上,因此不惜去骗取她的爱情。

大班社会教案:会说话的标志
2、通过看看,说说,做做,让幼儿了解标志有不同的含意,知道生活中许多地方都离不开它,从而丰富幼儿的生活经验,增强幼儿自我保护意识。 活动准备 配合进行教育活动的多媒体课件,幼儿制作标志的纸、笔等、供幼儿张贴的标志若干。 活动过程:1、观看多媒体课件,引起幼儿活动的兴趣。 教师提问:这里有些什么?从哪里看出来的?2、教师小结:看到了这些标志,就知道这是哪里了。标志是各种各样的,代表了不同的意思。如:看到红“+”,就知道是医院,看见大滑梯等玩具就知道是幼儿园……3、请幼儿观看课件中的标志,并说出你在哪见过?它告所我们什么?(教师可为幼儿准备一些交通标志、安全标志等)

中班安全教案:会说话的安全标志
活动目标: 1、鼓励幼儿探索学习,使幼儿认清安全标志,教育幼儿不要玩火、电等危险物品,遵守交通规则。 2、引导幼儿发现尝试,让幼儿知道应该按照安全标志的要求行动,才能既方便自己又不影响集体,培养自我保护意识和能力。 3、通过幼儿自己动手制作安全标志,发展幼儿的想象力和创造力及动手制作的能力。 活动准备: 1、多媒体课件:交通安全、严禁烟火、当心触电、禁止触摸等内容的小故事,并配有关的安全标志。 2、事先让幼儿收集有关的安全标志。 3、每幼儿一套安全标志七种:注意安全、人行横道、步行、禁止通行、严禁烟火、当心触电、禁止触摸。 4、画纸、水彩笔、剪刀等工具材料。

幼儿园大班歌唱教案:戏说脸谱
2.学习根据不同的脸谱角色,用合适的力度及动作来表现人物的性格特征。 3.初步了解中国国粹——京剧艺术,并逐步喜爱京剧艺术。活动准备 1、知识经验:邀请家长共同协助帮助幼儿欣赏有关京剧表演的flash、认识各种不同色彩的京剧脸谱、了解与活动内容有关的各人物特征等, 2、物质准备:京剧脸谱课件:蓝脸、红脸、花脸、白脸、黑脸。 歌曲内容小图片;幼儿自制京剧脸谱若干。 活动过程 1、说脸谱 (1)师幼共同欣赏京剧脸谱课件,说说各种不同脸谱所代表的人物名称及其性格特征。

中班科学教案:怎样悄悄对你说
2、学习自制传话筒,提高动手能力。 【活动准备】 各种声音的录音;铃鼓、锣、三角铁、尺子、皮筋、塑料袋、筷子、吉他等;纸杯、棉线、透明胶带。 【活动过程】 1、播放各种声音的录音,引起幼儿的兴趣。 提问:“你听到了什么?” 2、引导幼儿尝试用各种方法使物体发出声音。 (1)提供各种物体,引导幼儿观察。 提问:“这些东西不动时,它能发出声音吗?”“你能用什么办法使它们发出声音呢?”

大班科学教案:会说话的标记
2,培养幼儿关注周围事物的习惯,探索周围事物的兴趣。 活动准备; 1,各种常见的标志。家长有意识的带领幼儿观察过各种标志。 2,背景图二幅。 3,纸、记号笔、蜡笔人手一份。 活动重点:了解各种标志的不同含义。 活动难点:能尝试制作生活中所需的标志。 活动流程:理解各种标志——学会运用标志——尝试制作标志——延伸活动 活动过程: 一,理解各种标志 1,出示标志背景图,观察: 1)这里有什么?从哪里看出来的?(重点让幼儿描述医院、麦当劳二个标志) 2)小结:看到了这些标志,就知道这是哪里了,标志是各种各样的,各种不同的标志代表不同的意思。

大班科学教案:会说话的标志
2.培养幼儿关注周围事物的习惯,探索周围事物的兴趣。 活动流程: 理解各种标志-->学会运用标志-->制作生活中所需的标志 材料与环境创设: 标志的背景图 活动指导: 一、理解各种标志(知道什么是标志,了解标志是各种各样的。) 1.这里有些什么?从哪里看出来的?(重点让幼儿描述医院,麦当劳和红星幼儿园三个标志) 2.小结:看到了这些标志,就知道这是哪里了。标志是各种各样的,代表了不同的意思。

大班安全教案:会说话的安全标志
活动目标: 1、鼓励幼儿探索学习,使幼儿认清安全标志,教育幼儿不要玩火、电等危险物品,遵守交通规则。 2、引导幼儿发现尝试,让幼儿知道应该按照安全标志的要求行动,才能既方便自己又不影响集体,培养自我保护意识和能力。 3、通过幼儿自己动手制作安全标志,发展幼儿的想象力和创造力及动手制作的能力。 活动准备: 1、多媒体课件:交通安全、严禁烟火、当心触电、禁止触摸等内容的小故事,并配有关的安全标志。 2、事先让幼儿收集有关的安全标志。 3、每幼儿一套安全标志七种:注意安全、人行横道、步行、禁止通行、严禁烟火、当心触电、禁止触摸。 4、画纸、水彩笔、剪刀等工具材料。

