-

北师大初中九年级数学下册弧长及扇形的面积教案
1.了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用;(重点)2.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长l=nπR180和扇形面积S扇=nπR2360的计算公式,并应用这些公式解决一些问题.(难点)一、情境导入如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14,所以铁轨的长度l≈2×3.14×1004=157(米). 如果圆心角是任意的角度,如何计算它所对的弧长呢?二、合作探究探究点一:弧长公式【类型一】 求弧长如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()
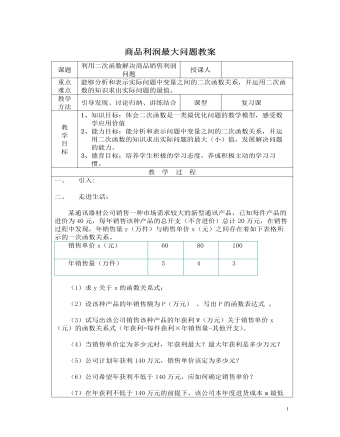
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册二次函数与一元二次方程1教案
解:(1)设第一次落地时,抛物线的表达式为y=a(x-6)2+4,由已知:当x=0时,y=1,即1=36a+4,所以a=-112.所以函数表达式为y=-112(x-6)2+4或y=-112x2+x+1;(2)令y=0,则-112(x-6)2+4=0,所以(x-6)2=48,所以x1=43+6≈13,x2=-43+6<0(舍去).所以足球第一次落地距守门员约13米;(3)如图,第二次足球弹出后的距离为CD,根据题意:CD=EF(即相当于将抛物线AEMFC向下平移了2个单位).所以2=-112(x-6)2+4,解得x1=6-26,x2=6+26,所以CD=|x1-x2|=46≈10.所以BD=13-6+10=17(米).方法总结:解决此类问题的关键是先进行数学建模,将实际问题中的条件转化为数学问题中的条件.常有两个步骤:(1)根据题意得出二次函数的关系式,将实际问题转化为纯数学问题;(2)应用有关函数的性质作答.

北师大初中九年级数学下册确定二次函数的表达式1教案
解析:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,根据对称轴是x=-3,求出b=6,即可得出答案;(2)根据CD∥x轴,得出点C与点D关于x=-3对称,根据点C在对称轴左侧,且CD=8,求出点C的横坐标和纵坐标,再根据点B的坐标为(0,5),求出△BCD中CD边上的高,即可求出△BCD的面积.解:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,∴c-4b=-19.∵对称轴是x=-3,∴-b2=-3,∴b=6,∴c=5,∴抛物线的解析式是y=x2+6x+5;(2)∵CD∥x轴,∴点C与点D关于x=-3对称.∵点C在对称轴左侧,且CD=8,∴点C的横坐标为-7,∴点C的纵坐标为(-7)2+6×(-7)+5=12.∵点B的坐标为(0,5),∴△BCD中CD边上的高为12-5=7,∴△BCD的面积=12×8×7=28.方法总结:此题考查了待定系数法求二次函数的解析式以及二次函数的图象和性质,注意掌握数形结合思想与方程思想的应用.

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

北师大初中九年级数学下册圆内接正多边形教案
解析:正多边形的边心距、半径、边长的一半正好构成直角三角形,根据勾股定理就可以求解.解:(1)设正三角形ABC的中心为O,BC切⊙O于点D,连接OB、OD,则OD⊥BC,BD=DC=a.则S圆环=π·OB2-π·OD2=πOB2-OD2=π·BD2=πa2;(2)只需测出弦BC(或AC,AB)的长;(3)结果一样,即S圆环=πa2;(4)S圆环=πa2.方法总结:正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径、外接圆半径、边心距,中心角之间的计算转化为解直角三角形.变式训练:见《学练优》本课时练习“课后巩固提升”第4题【类型四】 圆内接正多边形的实际运用如图①,有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心(下列各题结果精确到0.1m).(1)求地基的中心到边缘的距离;(2)已知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?

北师大初中九年级数学下册圆周角和圆心角的关系教案
解析:点E是BC︵的中点,根据圆周角定理的推论可得∠BAE=∠CBE,可证得△BDE∽△ABE,然后由相似三角形的对应边成比例得结论.证明:∵点E是BC︵的中点,即BE︵=CE︵,∴∠BAE=∠CBE.∵∠E=∠E(公共角),∴△BDE∽△ABE,∴BE∶AE=DE∶BE,∴BE2=AE·DE.方法总结:圆周角定理的推论是和角有关系的定理,所以在圆中,解决相似三角形的问题常常考虑此定理.三、板书设计圆周角和圆心角的关系1.圆周角的概念2.圆周角定理3.圆周角定理的推论本节课的重点是圆周角与圆心角的关系,难点是应用所学知识灵活解题.在本节课的教学中,学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握,理解起来问题也不大,而对圆周角与圆心角的关系理解起来则相对困难,因此在教学过程中要着重引导学生对这一知识的探索与理解.还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题,在教学过程中要对此予以足够的强调,借助多媒体加以突出.

北师大初中九年级数学下册直线和圆的位置关系及切线的性质教案
解析:(1)由切线的性质得AB⊥BF,因为CD⊥AB,所以CD∥BF,由平行线的性质得∠ADC=∠F,由圆周角定理的推论得∠ABC=∠ADC,于是证得∠ABC=∠F;(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,然后运用解直角三角形解答.(1)证明:∵BF为⊙O的切线,∴AB⊥BF.∵CD⊥AB,∴∠ABF=∠AHD=90°,∴CD∥BF.∴∠ADC=∠F.又∵∠ABC=∠ADC,∴∠ABC=∠F;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°.由(1)可知∠ABF=90°,∴∠ABD+∠DBF=90°,∴∠A=∠DBF.又∵∠A=∠C,∴∠C=∠DBF.在Rt△DBF中,sin∠DBF=sinC=35,DF=6,∴BF=10,∴BD=8.在Rt△ABD中,sinA=sinC=35,BD=8,∴AB=403.∴⊙O的半径为203.方法总结:运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

大班科学教案:谁能穿越管子
活动准备: 不同形状的白色弯管若干,一段既有螺帽的尼龙线、打气筒、铅笔、手电筒若干,直管弯管若干,幼儿实验记录表若干,教师实验记表一张。 活动过程:1、出示直管。 师:这是什么?平时有什么东西可以穿越这根直管? 师:今天老师给你们带来了四样东西,它们分别是一端系由螺帽的线、打气筒、铅笔、会发光的手电筒,(一端系由螺帽的线、打气筒、铅笔、会发光的手电筒)你们来猜猜看,这些东西他们哪些能穿越直管,哪些不能?(幼儿猜测) 师:让我们动手做个实验试一试吧!老师为你们准备了实验级路标,你们可以把实验中的发现记录下来,能穿越直管的,就在表格后面这里打个“勾”如果不能得就打个“叉”。

大班科学教案:闻气味的鼻子
2、教育幼儿要保护好自己的鼻子。 3、培养幼儿积极运用感官的习惯。 活动准备 不透明的容器,分别装有香水、大蒜、麻油、醋、酒、橘子等,最好每组一套。 活动过程 1、出示大象的木偶。小朋友你们说大象的鼻子有什么用处? (大象的鼻子能卷东西) 出示狗的木偶。小朋友,狗的鼻子又有什么用处? (狗的鼻子最灵)。 2、讨论人的鼻子有什么用处。 ⑴、动物的鼻子有这么大用处,那么我们人的鼻子有什么用呢?(呼吸、嗅气味) ⑵、桌上有许多小瓶子,用我们的小鼻子来闻闻,看瓶子里装的是什么。 ⑶、说说你最喜欢什么气味,不喜欢什么气味,为什么?你以前还闻过哪些有气味的东西?

大班音乐教案:《会跳舞的叶子》
2、用正确的节奏歌唱。活动准备录音机、钢琴。活动过程一、谈话法1、小朋友,你知道大树妈妈最爱什么?你见过树叶从树上往下飘落的样子象什么?2、邀请幼儿边念儿歌边做暖身操,如下: 1 2 3双手放下 双手平举 双手高举

幼儿园音乐教案:打击乐《鸽子》
2、创编鸽子飞翔、唱歌等模仿动作随音乐表演。 3、了解信鸽的特点,加深爱鸽子的情感。活动准备 铃鼓、碰铃、圆舞板等乐器人手一件。活动过程 1、复习歌曲《邮递员叔叔》。 1)齐唱歌曲。 2)边唱边做即兴表演。 2、谈话:“会送信的鸽子”。

幼儿园大班教案:大雁和鸭子
活动准备: 1、多媒体课件、录音机、磁带。 2、提前布置好春、夏、秋、冬的场景。 3、绘画工具、布偶。 活动过程:一、教师以“故事多多姐姐”的身份出场,自我介绍。 1、“我”教师走进教室. 2、“我”教师:小朋友们好!还认识我吗?(幼答)我是来自动画城的多多姐姐,自从我们栏目举办了“幸运星旅行记”以来,收到了很多小朋友的来信与参与。今天很高兴来到这里,并恭喜你们成为本周的幸运星,一起加入我们的幸运星旅行吧!(给幼儿佩带幸运星饰品)我们的口号是“故事多多,乐趣多多”,那么今天我们旅行的第一站就是动 画城,跟我出发吧!(随音乐一起入场)

大班科学教案:水流到别的杯子去
1:提供不同材料,建议幼儿思考如何使沉入水中的材料浮于水面,或使浮于水面的材料沉入水中。如用牙膏皮做成小船,或将小铁钉放在积木上等。沉与浮 2(立起来的木棍):将小木棍放入水中,发现它躺在水面上。如果在木棍一端粘一大块橡皮泥,或钉上一根大铁钉,都能使它立起来。 活动目标:使用多种材料,玩水的过程充满和有趣。 活动材料:饮料管、纸、牙膏皮、泡沫塑料、小积木、塑料、菜叶、小瓷器、竹片、铁钉、小石子水管、竹片、盛水具、彩色墨水等 活动过程:下午天气热,小朋友都在玩水。今天材料很丰富,但给出一个条件,每人只给一盆水,要节约用水,用完就没有了。用水管连接水的有3组、用大小杯子滔水的有2组、用矿泉水瓶盖扎洞来射水有3组、做水帘洞1组、沉浮和自定义玩法有几组。 “水流到别的杯子去”组;佘馨蕊、张俊骞、覃芷珊、卢艺文、班学佳 *这几个小朋友,把2根管子把3个杯子连接起来,慢慢地将一杯红色的水倒在水杯里玩,发现杯里的红水通过连接饮料管子流到另一个水杯,3杯水慢慢变红了,孩子们高兴极了,饮料管子传送水耶,3杯红水第一次出现流动成水平,水不流动了。

大班音乐教案:小音符的房子
活动目的:1、通过游戏让幼儿认识五线谱,知道构成五线谱的元素线、间、小节线以及高音谱号的名称。2、让幼儿自由在五线谱上建构的乐谱,并能说出自己在五线谱的位置。3、培养幼儿的音乐素养,激发幼儿对音乐的兴趣。4、让幼儿体验互相帮助,共同合作的乐趣,培养幼儿充分的自信心和成功感。 活动准备:1、音符头饰。2、五线谱图示。3、制作五线谱的毛线,将若干小节线、高音谱号放在教室周围。

中班健康教案:做个讲卫生的好孩子
2、通过讨论及知识竞赛的形式、知道如何做一名将卫生的孩子。 3、知道讲卫生可以给自己和他人带来愉快的情绪、同时也会受到大家的欢迎的。 活动准备: 1、有关个人卫生和环境卫生的知识竞赛题、 2、教师演唱歌曲《猪小弟》 3、五角星贴花若干。 活动过程: 一、教师讲述故事,引出主题 今天老师带来了一个故事《小猪变干净》 师讲述故事后提问:猪小弟为什么找不到朋友玩游戏?为什么它身上脏,大家就不愿意和它玩呢?最后,它为什么能找到朋友玩?

大班科学教案:各种各样的管子
整个过程我分为三个阶段:1、设疑激趣,巧妙导入。 我选择了在开始部分用课件的形式向幼儿展示各种用管子制成的艺术品,激发幼儿探究的兴趣。2、师幼参与,探索认知。 本阶段是整节课的重点。在活动中,我坚持以幼儿为本,启发引导幼儿大胆想象,让他们尽情发挥,积极发言。通过认一认、分一分、说一说、做一做等活动,认识各种各样的管子,学习对管子进行简单分类,了解管子的重要性,能爱惜管子,不向管子形状的通道中乱扔东西。3、活动延伸,培养能力。 在活动即将结束时,我准备让幼儿大胆地想象,亲自动手制作一件管子作品,创造性的玩管子,以培养幼儿的想象力和动手操作的能力。【活动目标】1、了解各种各样的管子在日常生活中的应用,能根据管子的特点对管子进行简单的分类。2、知道管子给人们的生活带来了方便,不向管道中乱扔东西。3、会用管子进行简单的造型,会玩各种管子游戏,感受管子游戏的乐趣。

大班科学教案:杯子怎么会流汗
二、活动目标:1、让幼儿通过实验了解露水、雨是如何在空气中形成的。2、培养幼儿的探索兴趣,发展他们的动手操作及观察能力。3、引导幼儿用语言表达在探索和发现中的感受。三、活动准备:人手一个干净的空玻璃杯、杯盖、一盘甜冰块<BR><P></P>四、活动流程:设疑导入记录猜想幼儿实验拓展经验

