-

人教版高中政治必修4价值判断和价值选择说课稿(一)
2.讲授新课:(约35分钟)结合教材内容重难点和学生实际,在讲课过程中,我对教材内容的顺序进行了重组,把教材内容由原来的两大部分划分为三大部分(第一,价值判断和价值选择的含义和关系;第二,价值判断和价值选择的特征;第三,做出正确的价值判断和价值选择的标准)。这一调整更符合学生的认知结构,便于从整体上把握课本内容。在讲授过程中,我充分利用课本素材——探究活动为课堂教学服务,此外,利用学生的生活与体验,挖掘实例,如结婚要礼由以前的旧三件到现如今的转变,引导学生理解价值判断和价值选择的社会历史性特征,以以《观祈雨》、以医生、艺术家、老学究对于《断臂的维纳斯》这个雕塑的不同见解、以新鲜实例韩国沉船事件和范跑跑为例启发学生价值判断和价值选择具有主体差异性特征以此突破难点,最后通过设疑、对比、追问正确的价值判断和价值选择的标准来深化主题,突出重点。3.课堂小结:(约2分钟)强化认识

人教版高中政治必修4认识运动把握规律说课稿(一)
(7)精讲即精讲点拨,释疑解难。现代教育理论一方面强调学生学习的主动性;另一方面也重视发挥教师的积极性。课堂活动的主动性、合理性、有效性的实现还有赖于教师的讲。精讲就要求教师的讲授内容精要,分析精辟,语言精彩、节奏精练、点拨精当。从内容上看,本节课精讲主要有三处:一、运动的含义;二、运动是物质的根本属性;三、静止是运动的特殊状态。2、教学手段多媒体辅助教学。六、教学过程第一步:创设情景,用“谜语”导入新课。使学生置身于教学内容的情景之中,产生继续探究的强烈愿望。第二步:运用直观、形象的画面将教学目标问题,唤起学生参与欲望,驱使学生去思考,去自读。第三步:引导学生相互讨论,实现学生之间的横向交流。第四步:教师依据反馈信息,给予重点讲授、提示点拨、搭桥铺路。第五步:设置故事型的模拟法庭,开展讨论,在高潮中结束新课。第六步:总结概括,深化知识,形成网络。

人教版高中地理必修1第二章第一节冷热不均引起大气运动说课稿
4、【自主探究】巴山夜雨的成因③材料三:三国时期,诸葛亮于农历6月的一天,在葫芦峪设下伏兵,打算用火攻全歼司马懿。这一天,晴空万里暑热难耐,真乃火攻之良机。诸葛亮依计将司马懿之众诱入谷中……然而,正当大火冲天,司马懿全军行将覆灭之时,一场大雨不期而至,大雨浇灭了诸葛亮扶汉反魏的壮志,使他喊出了“谋事在人,成事在天,不可强也”的千古悲歌。【设计理念】前后呼应,发散思维。通过自主探究,学生各抒己见,完成对热力环流整个知识框架的一个总结,既考查了学生的课堂学习效果,又锻炼了学生知识的迁移能力,并认识生活中的地理规律,用生动的语言拉近学生与大气理性知识的距离,体会到地理学科的重要性。【提问】如果将白天换成夏季,将夜间换成冬季,情况又会怎样?城市与郊区之间也存在着热力环流——城市风,它们是怎样形成的?了解城市风的出现有何重要意义?如果地球上在赤道和两极之间存在热力环流,这个热力环流应该怎样?这几个问题,请大家课后慢慢思考。

“3·15”国际消费者权益日国旗下讲话稿: 3·15与诚信
三月有许多有意义的日子,比如刚刚过去的3月5日学雷锋日;3月12日植树节。今天,我们说一说即将到来的“3·15”国际消费者权益日。对于“3·15”消费者权益日,许多同学不陌生。平时,在各类媒体上,在我们身边、在我们自己的亲身经历中,都有许多关于消费的愉快与不愉快。而消费的满意与不满意最根本的原因就是商家是否“诚信”。因此,许多人认为:“3·15”也是诚信日。诚信日?只要求商家诚信吗?在社会中,我们每个人都是消费者,也是各种看的见或者看不见的产品的制造者。所以我们人人都应该讲诚信,人人都应该关注并保障对方的利益。什么是诚信?百度里说:诚信是公民的第二张身份证,是为人处事,真诚而不虚假,老实而不矫情;是一言九鼎,是一诺千金。我们同学在校园里,如何践行诚信?

第九周国旗下讲话稿:学会自我保护,安全与我同行
尊敬的老师们,同学们:Dearteachersandclassmats,大家早上好!我是二(1)班的张xx。今天我演讲的主题是《学会自我保护,安全与我同行》。Goodmorning!Iam______fromclass1Grade2.mytopicis“Tolearnhowtoprotectmyself,tobesafeeverytime”.校园是我们共同学习的地方,这里有老师,有同学,在这个大家庭里,我们快乐地学习,健康地成长。但是,在这个大家庭里,也很容易发生意外。campusisaplacewestudytogether.Thereareteachersandstudentshere,westudyhappilyandgrowhealthily.However,wemeetaccidentsometimes,too.午觉过后,有同学奔跑着回到教室;课间十分,有同学在教室走廊里追逐打闹……像这样不看路,快速奔跑都是非常危险的,严重的还会骨折。我曾经看到一位高年级的大哥哥,下课铃一响,他就飞快地从教室冲出来,快到直饮水机旁边时,因为跑得太快,他没看到脚下有东西,摔倒在地上,送到医院一看,已经骨折了,好多天都没来上学,不光耽误了功课,还受了许多罪。

第十二周国旗下讲话稿:冬季长跑,让健康与我同行
第十二周国旗下讲话:冬季长跑,让健康与我同行尊敬的老师、亲爱的同学们:大家好!我是高一15班的雷xx。今天我国旗下讲话的题目是:冬季长跑,让健康与我同行。在这个金桔飘香的季节里,同学们,你们是否听见了冬天的脚步在向我们临近?随着冬天的到来,皮肤干燥、饮食减少、伤风感冒等各种疾病也随之而来。我想从此时开始,我们全校师生应该树立起“健康第一”的观念,享受阳光下美好的时光,利用好这些时间积极投身体育活动,强健我们的体魄。为此,我对深入持久的开展阳光体育冬季长跑提出以下几点希望:一、在活动中加强“诚信”的自我教育,提高自我锻炼意识和参与意识,促进学校体育活动健康积极发展。二、条件受限形式可变,长跑并非是唯一的锻炼方式,同学们要结合实际情况,开展形式多样的体育活动,关键在于运动。

第五周国旗下讲话稿:孩子成绩好坏,居然与抽屉有关
中国教育报官方微信3月20日有一篇《一位校长惊人发现:孩子成绩好坏,居然与抽屉有关》。杭州实验外国语学校新学期有了一条新规定:学生抽屉整理的合格率达到95%以上的,班级任课教师可以集体拿到500元;合格率达到100%的,而且优秀率是年段最高的,可以获得学习习惯示范班级的荣誉。为什么要新增这样一条规定?中举了这样两个案例。下沙中考状元赵俊皓,抽屉无论什么时候都是最整齐的。不管你问他要什么资料,他都能准确说出在抽屉中的位置,并且第一时间取出。照他自己的理论就是“抽屉整齐,脑子清爽”。有一个男生,成绩还行,习惯很差,上节课发的试卷,下节课老师要讲评了,他竟然找不到了,即使找到了,也是一团纸,打开来是皱巴巴的。他的抽屉里,乱七八糟的东西很多,找一本作业本,要把抽屉里的东西都拿出来,像摆地摊一样。

国旗下的讲话演讲稿:学会设计人生的价值观
演讲稿频道《国旗下的讲话演讲稿:学会设计人生的价值观》,希望大家喜欢。各位尊敬的老师,亲爱的同学们:大家上午好!同学们,人生的目标不妨定的高远些,如果经过全力打拼,没有实现,那么至少也要比目标定的太低的人实现得多。林肯曾经说过:“喷泉的高度不会超过他的源头,一个人的事业也是这样,他的成就绝不会超过他的信念”。当拿破仑还是个少尉的时候,工作之余,他的同伴们便开始寻欢作乐,去游玩或找女人。他却在埋头读书,如饥似渴地读那些对他将来有用的东西:历史、战争、哲学、文化、法律、天文、地理、气象学等等。他曾说过:“不想当元帅的士兵不是个好士兵”。

国旗下的讲话演讲稿:奋斗的人生最美丽
这篇《国旗下的讲话演讲稿:奋斗的人生最美丽》,是特地,希望对大家有所帮助!沧海桑田,岁月无声。历史老人就像是一位顽强奋斗而永远年轻的玩世大侠,它催逝了往者,又孕育了新军。那凡夫俗子如过往云烟飘然而逝,唯有奋斗者,才是浩瀚星河中永不陨落的灿烂星辰!历史的天空闪烁几颗星星,人间一股英雄气在驰骋纵横。看,梁启超,改良的斗士;孙中山,民主的先驱;毛泽东,新中国的;邓**,改革开放的总设计师。巨星耀银河,美名传千古,不因为他们是伟人,而在于他们在成就大业的过程中能面对逆境,舍生取义,百折不挠,倔强挺立。梁启超,科举落地而偏不重演孔乙己的悲剧;孙中山,大革命失败而高呼“同志还需努力”;毛泽东,在被围追堵截的逃亡中依然从容地四渡赤水;邓**,九十高龄的老人却能在谈笑中换来春风春雨。伟人的奋斗固然可以传为佳话,平凡人的奋斗也许更能触发我们感慨动容。为了孩子的成长,我们的父母长年累月风雨兼程给我们送佳肴和棉衣——那翘首祈盼的焦急神情看得出好疼爱你们啊;为了我们的前途,班主任几十年如一日和我们朝夕相处甚至相濡以沫——拖着疲倦的身子离开宿舍,眼睛却不时回望本班的寝室

国旗下的讲话稿:专心致志,做学习的主人
这篇《国旗下的讲话稿:专心致志,做学习的主人》,是特地,希望对大家有所帮助!老师们、同学们:大家好!今天我演讲的题目是《专心致志,做学习的主人》。满怀着憧憬和希望,我们开始了新学期,这是一个能让我们实现理想,见证成长的一个学期。然而,激越澎湃之后,随之而来的却不尽是欢声与笑语,学习上虽然有着快乐,却已不再轻松,面对着一个个强手,看着他们的出类拔萃和独立张扬的个性,你或许自卑,或许哀叹,甚至怨恨自己的不争,但是,千万不要放弃,要坚信,只要有付出,就一定会有回报。随着新课改的全面展开,和XX、XX年高考新方案的公布,学习和生活都向我们敞开了新天地,也给了我们的挑战。每一位同学都要随时根据阶段考试的结果,和老师们的指导适时进行调整,不要自以为是,只埋头学习,不明确方向。这就要求我们要从现在起:首先,要养成上课积极思考,踊跃表达,质疑问难的良好习惯,只有这样,大家集思广益,相互交流,不仅有立于打破狭隘的思维界限,拓宽四位空间,而且还能增强相互合作和交流的能力。
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点

【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 我们知道,在直角三角形(如图)中,,,即 ,, 由于,所以,于是 . 图1-6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中,是否也存在类似的数量关系呢? c 图1-7 当三角形为钝角三角形时,不妨设角为钝角,如图所示,以为原点,以射线的方向为轴正方向,建立直角坐标系,则 两边取与单位向量的数量积,得 由于设与角A,B,C相对应的边长分别为a,b,c,故 即 所以 同理可得 即 当三角形为锐角三角形时,同样可以得到这个结论.于是得到正弦定理: 在三角形中,各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题: (1)已知三角形的两个角和任意一边,求其他两边和一角. (2)已知三角形的两边和其中一边所对角,求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.1《排列与组合》优秀教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 3.1 排列与组合. *创设情境 兴趣导入 基础模块中,曾经学习了两个计数原理.大家知道: (1)如果完成一件事,有N类方式.第一类方式有k1种方法,第二类方式有k2种方法,……,第n类方式有kn种方法,那么完成这件事的方法共有 = + +…+(种). (3.1) (2)如果完成一件事,需要分成N个步骤.完成第1个步骤有k1种方法,完成第2个步骤有k2种方法,……,完成第n个步骤有kn种方法,并且只有这n个步骤都完成后,这件事才能完成,那么完成这件事的方法共有 = · ·…·(种). (3.2) 下面看一个问题: 在北京、重庆、上海3个民航站之间的直达航线,需要准备多少种不同的机票? 这个问题就是从北京、重庆、上海3个民航站中,每次取出2个站,按照起点在前,终点在后的顺序排列,求不同的排列方法的总数. 首先确定机票的起点,从3个民航站中任意选取1个,有3种不同的方法;然后确定机票的终点,从剩余的2个民航站中任意选取1个,有2种不同的方法.根据分步计数原理,共有3×2=6种不同的方法,即需要准备6种不同的飞机票: 北京→重庆,北京→上海,重庆→北京,重庆→上海,上海→北京,上海→重庆. 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 15*动脑思考 探索新知 我们将被取的对象(如上面问题中的民航站)叫做元素,上面的问题就是:从3个不同元素中,任取2个,按照一定的顺序排成一列,可以得到多少种不同的排列. 一般地,从n个不同元素中,任取m (m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列,时叫做选排列,时叫做全排列. 总结 归纳 分析 关键 词语 思考 理解 记忆 引导学生发现解决问题方法 20
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
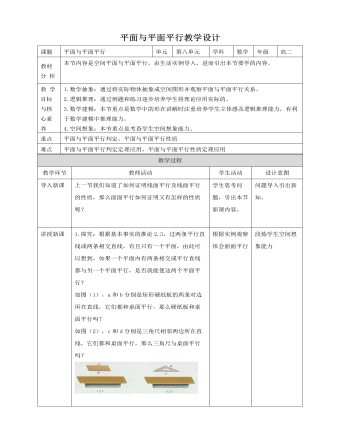
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
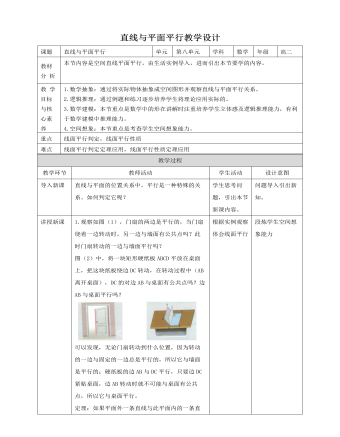
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

北师大版初中七年级数学下册用尺规作三角形说课稿
《用尺规作三角形》是北师大版《义务教育课程标准实验教科书.数学》七年级下册第五章第五节的内容。在之前的学习中,我们已经学会用尺规作线段和角,而边和角是三角形的基本元素,这节课主要是学习利用尺规按要求做三角形,表面上看是操作的过程,但教科书中提出了有关探究性问题,目的是引导学生关注作图背后的数学思考,即用尺规作三角形用到了两个三角形全等的条件,因此本课教学应引导学生积极思考,使学生体会到作图的每一步骤都是有根 有 据的.二、教学目标分析参照《课程标准》的要求及教材的特点,考虑到学生已有的认知结构和心理特征 ,我制定了如下教学目标:1、知识与技能:1.会用尺规按要求作三角形:已知三边作三角形,已知两角及夹边作三角形,已知两边及夹角作三角形.2.会写出三角形的已知、求作、作法. 3.能对新作三角形给出合理的解释.

