-
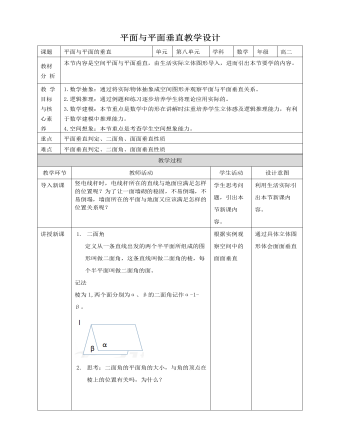
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
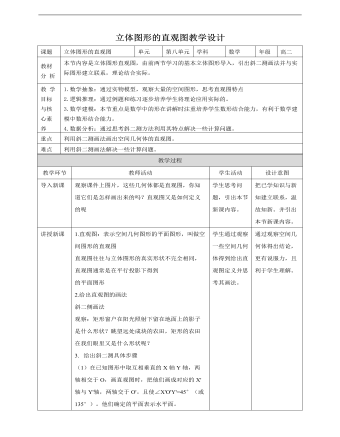
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
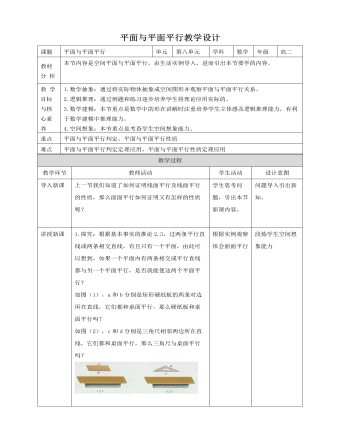
人教A版高中数学必修二平面与平面平行教学设计
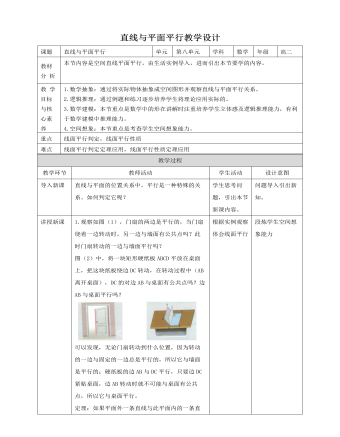
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
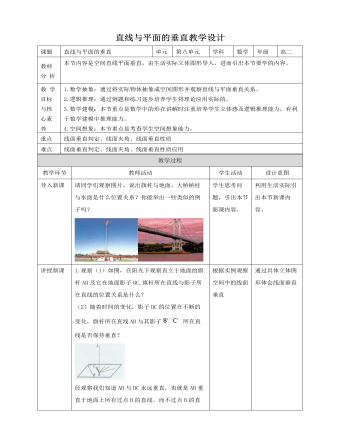
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

人教版高中数学选择性必修二变化率问题教学设计
导语在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识,定性的研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长” 是越来越慢的,“指数爆炸” 比“直线上升” 快得多,进一步的能否精确定量的刻画变化速度的快慢呢,下面我们就来研究这个问题。新知探究问题1 高台跳水运动员的速度高台跳水运动中,运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+4.8t+11.如何描述用运动员从起跳到入水的过程中运动的快慢程度呢?直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动的越来越慢,在下降阶段运动的越来越快,我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度v ?近似的描述它的运动状态。

观看央视《灯塔大课堂第28课》心得体会范文精选
朔风凛冽,气温低至零下二十多摄氏度。出发前,同志们都穿上了配发的空军地勤服——皮上衣、皮裤子。郭永怀个头偏高,没有合适的尺寸。大家劝他留在家里,等候答复,可他无论如何不答应。人们拗不过他,只好找来一件皮大衣和一双毛皮靴凑合穿。实验场区没有帐篷,也没有座椅。站乏了,冻透了,只能咬牙坚持。终于挨到开饭时间,郭永怀和大伙一样,用开水把冻得硬邦邦的馒头泡软,就着咸菜,凑合一顿。 在研发过程中,对于引爆方式的选择,科研人员一度在较易实施的“枪式法”和起点较高的“内爆法”之间难以取舍。郭永怀采用“特征线法”进行理论计算,提出以先进的“内爆法”作为主攻方向,同时,为了稳妥起见,应当“争取高的,准备低的”。随后进行的爆轰物理实验无疑是掌握关键技术的重要一环,为了取得满意的爆炸模型,郭永怀带领科研人员反复试验,有时,甚至跑到帐篷里亲自搅拌炸药……

大班综合体育课《小猴寻宝》课件教案
2、培养幼儿动手操作能力、协作能力、团队协作能力。3、复习10以内的数的顺序及找规律。活动准备:每个幼儿一个小猴头饰、桃子和苹果图片、桌子、画有飞机和汽车的卡片各一大张并分成和幼儿人数的一半的份数、玩具若干、录了《猴哥》音乐的磁带、小鸟头饰一个、老虎头饰两个。活动过程:1、猴妈妈和孩子们在睡梦中醒来, 猴妈妈带着孩子们在“猴哥”的音乐声中进行晨练。(做热身运动)2、 孩子们都饿了,妈妈带着孩子们到树林去摘果子(练习跳高)。在孩子们吃果子时,一只小鸟飞来说道:“猴妈妈,听说五台山上有宝藏,许多小动物都去寻宝去了,你们也快去吧!”然后飞走了。

代课教师劳动合同
三、工作报酬、保险与福利待遇第五条甲方根据乙方的工作岗位,按月支付乙方的工资。乙方试用期工资为___元/月,正式聘用期工资由基本工资和绩效工资组成,基本工资为___元/月。绩效工资按甲方依法确定的分配制度、方式和标准执行。如甲方的工资制度发生变化或乙方的工作岗位变动,按新的工资标准确定,并根据乙方的工作岗位,确定每月工资报酬。第六条乙方在甲方处工作满一个学期后可以享受寒暑假的带薪假期。寒暑假只发基本工资___元/月。合同期限届满后甲乙双方不续签合同的,甲方不支付该寒暑假工资。

小学课程工作计划
1、保持学生对音乐的兴趣,使学生乐于参与音乐活动。 2、培养音乐感受与鉴赏能力。 3、培养表现音乐的能力。 4、培养艺术想象和创造力。 5、培养乐观的态度和友爱精神

高二备课组工作计划
(1)集体备课,教学流程基本统一。每次备课组活动都必须对下周所上内容进行讨论,如何上,深度如何,具体到每一个课时。同时,根据各层次的具体情况,适当进行调整,以适应学生的实际情况为标准,让学生学会、掌握并能运用。备课组要做到资源共享,反对个人主义。作业要求分层,必做题、选做题、拓展题,并注重作业反馈。

艺术课教学工作计划
①继续加强美术新课程标准和业务的学习,深化教学观念和理念 本学期,我将继续加强自身的业务培训,利用一切时间,多学,多练,多找自身的不足,多以课堂教学研讨为主要研究活动,加强自己对案例研究,使自己由认识新课程到走进新课程。

语文听课心得体会
在两节优质课中,教师放手让学生自主探究解决问题。每一节课,每一位老师都很有耐性的对学生有效的引导,充分体现“教师以学生为主体,学生是数学学习的主人,教师是数学学习的组织者,引导者和合作者”的教学理念。老师们的语言精炼、丰富,对学生鼓励性的语言十分值的我们学习、在思想教育方面,这些教师都处理的比较好,自然真挚的情感流露感染了学生和听课的每一位教师及家长。看到任欣和初艳丽两位语文老师气定神闲,信手拈来,不时激起一个个教学的浪花,不仅令学生陶醉、痴迷,更让我连声赞叹。从中我更深刻地体会到了学习的重要性与紧迫感。

实习老师听课心得体会
2.土地利用方式 通常,我国土地分为农用地、建设用地和未利用地。农用地是指直接用于农业生产的土地,包括耕地、林地、草地、农田水利用地、养殖水面等;建设用地是指建造建筑物、构筑物的土地,包括城乡住宅和公共设施用地、工矿用地、交通水利设施用地、旅游用地、军事设施用地等;未利用地是指农用地和建设用地以外的土地。在土地利用方式上,城镇与乡村明显不同,城镇以建设用地为主,乡村以农用地为主。 3.城乡土地利用 (1)城镇土地利用是指城镇中工业、交通、商业、文教、卫生、居住、绿化等建设用地的状况,反映的是城镇布局形态和空间功能差异。

矩形第1课时教案
1. 理解矩形的概念,明确矩形与平行四边形的区别与联系;2.探索并证明矩形的性质,会用矩形的性质解决简单的问题;3.探索并掌握“直角三角形斜边上的中线等于斜边的一半”这个定理.

幼儿园公开课教案复韵母ie
活动名称:复韵母ie授课教师:卡哇伊 活动目标:1,知道复韵母je的音、形以及四声调。 2,能够掌握标调规则,知道声调标在e上。 3.愿意尝试拼读音节,并组词。活动准备:复韵母e及四声调卡片各一张;音节卡片;若干声母卡片;“果树”一棵;筐子.活动重、难点:正确发出ie的音及四声调,拼读音节。

幼儿园语言课活动教案
第一课时: 一、活动准备: 1、幼儿园的背景图 2、儿歌中的动物图片 3、字卡 二、活动过程: (一)导入:师生谈话 1、小朋友们喜欢幼儿园吗? 2、表扬班上高高兴兴上幼儿园的小朋友,引出儿歌中的小动物。

家长学校授课教案
教学过程: 一、 导入。 尊敬的各位家长,你们好。首先欢迎你们来参加我们的家长会。感谢你们在百忙之中来到学校,共同来关注学生的学习情况,关心学生的发展情况。今天我们共同探讨的问题是怎样培养孩子的受挫能力。 二、 帮助家长们明确家长在家庭教育中培养学生健全人格的重要性。 要想引导未成年人走正确的人生道路,必须培养孩子做一个健全的人,要具有随时迎接挫折,迎接“丢脸”,经历痛苦的思想准备。这样的教育特别应该从小学生抓起,从小培养孩子们在挫折中成长的能力。因为,现在的孩子都是父母心中的“小皇帝”、“小公主”,他们从小在爷爷、奶奶、父母的精心呵护下长大,生活在太阳底下,吸取着雨露阳光。唯我独尊,娇横跋扈,事事占上风。试想,这样的孩子如果从小不接受正面的引导,能走正确的人生道路吗?他们只会遇到困难退却,受到挫折失去信心和希望,经受不了打击,他们只会顺水推舟,不会逆水行舟。难怪我国每年都会出现因不能正确面对父母的教育而服毒身亡的,因同学的嘲笑而跳楼自杀的,因学习的压力而弃学逃亡流浪街头的,因羡慕而产生妒忌走上犯罪道路的…… 因此,培养学生健全的人格是极为重要的。作为学校、家庭应责无旁贷加强培养孩子们从对挫折的能力,让他们在风雨中健康成长。

体育课安全教育教案
(一)导入 1、导言:同学们,你们看过足球比赛么?有什么感受?有没有危险呢? (1)学生各叙己见。 (2)教师归纳出示课题。 2、引导学生自主探索:体育课与课间活动应该注意那些安全事项? 学生讨论交流,各自发表。 (二)学习新知识 1、运动前的注意事项 (1)检查自己的身体情况 参加体育活动,首先要了解自己的身体状况,要学会自我监督,随时注意身体功能状况变化,若有不良症状要及时向教师反映情况, 采取必要的保健措施。切忌有心脏病或其他不适合参与体育活动的疾病而隐瞒病情,勉强参加活动。

