-

北师大初中七年级数学下册用科学记数法表示较小的数教案
方法总结:绝对值小于1的数也可以用科学记数法表示,一般形式为a×10-n,其中1≤a<10,n为正整数.与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数由原数左边起第一个不为零的数前面的0的个数所决定.【类型二】 将用科学记数法表示的数还原为原数用小数表示下列各数:(1)2×10-7; (2)3.14×10-5;(3)7.08×10-3; (4)2.17×10-1.解析:小数点向左移动相应的位数即可.解:(1)2×10-7=0.0000002;(2)3.14×10-5=0.0000314;(3)7.08×10-3=0.00708; (4)2.17×10-1=0.217.方法总结:将科学记数法表示的数a×10-n还原成通常表示的数,就是把a的小数点向左移动n位所得到的数.三、板书设计用科学记数法表示绝对值小于1的数:一般地,一个小于1的正数可以表示为a×10n,其中1≤a<10,n是负整数.从本节课的教学过程来看,结合了多种教学方法,既有教师主导课堂的例题讲解,又有学生主导课堂的自主探究.课堂上学习气氛活跃,学生的学习积极性被充分调动,在拓展学生学习空间的同时,又有效地保证了课堂学习质量
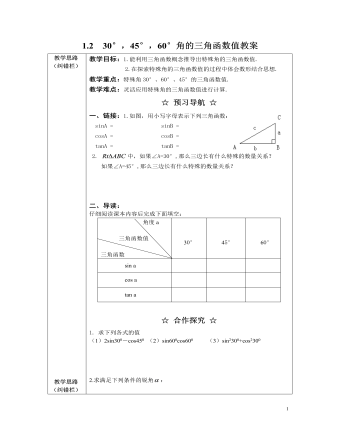
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?

北师大初中九年级数学下册利用三角函数测高2教案
问题2、如何用测角仪测量一个低处物体的俯角呢?和测量仰角的步骤是一样的,只不过测量俯角时,转动度盘,使度盘的直径对准低处的目标,记下此时铅垂线所指的度数,同样根据“同角的余角相等”,铅垂线所指的度数就是低处的俯角.活动三:测量底部可以到达的物体的高度.“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.要测旗杆MN的高度,可按下列步骤进行:(如下图)1.在测点A处安置测倾器(即测角仪),测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).根据测量数据,就能求出物体MN的高度.在Rt△MEC中,∠MCE=α,AN=EC=l,所以tanα= ,即ME=tana·EC=l·tanα.又因为NE=AC=a,所以MN=ME+EN=l·tanα+a.

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。
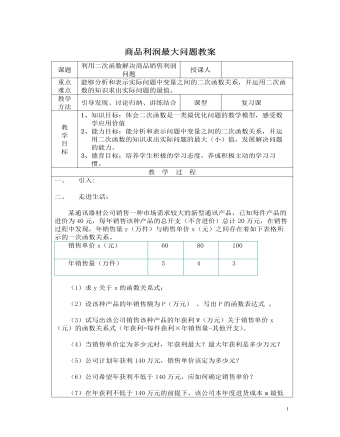
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

人教版新课标PEP小学英语四年级上册Recycle1教案2篇
Part two1. Teaching AimsMaster the 26 letters.Master the pronunciation of the letters.2. Teaching Aidsa tape-recorder, some cards, some papers and so on.3. Important pointsThe pronunciation of the letters4. Teaching steps1) Greetings and revisionLet some groups act out the dialogue in the last lesson.2) New contentsLet them say out the 26 letters and let some ones say them out.Then listen and learn the letters song.First, give them some minutes and let them read the letters. Let’s see whether there is anyone who can learn anything in them. Then give them some information and let them read again. At last, give them the answer and read again.Let them remember it.PracticeShow the cards where are written the math patterns and let some answer it. Then ask “Who can read it in English?” Let some one read it. Others follow him.Next, show the cards and ask others answer them. T asks and S answers. Then S asks and S answers. Practice in pairs.HomeworkMaster the letters.Teaching notesPart three1. Teaching AimsIntroduce self and others using the words and phrases.Let’s play.2. Teaching Aidsa tape-recorder, some cards3. Important pointsShe has…She likes…I have…4. Teaching stepsGreetings and revisionLet some one read the letters and divide them by the pronunciations.

人教版新课标PEP小学英语四年级上册My Friends教案2篇
1.叫一名学生在班里走动,站在一名学生的后面。 2.教师举起一张本单元的单词图片。先正确地说出这个单词第一个字母的读音的学生坐下,另一名学生继续在班里走动,继续活动。 板书设计 :My friends 黑板上方:上课前打好的四线三格,在课堂上随讲随写的字母Ww, Xx, Yy, Zz 黑板下方: 教案点评: 本课时主要学习字母Ww, Xx, Yy, Zz及相关单词。因为本课时将结束字母的学习,因此在热身、复习环节,有必要先进行字母Aa-Vv的听写。然后出示字母卡、单词卡让学生认读字母和复习单词。呈现新课环节,教师可将字母教学放到单词中进行。在教学过程 中,教师结合图片或实物逐个进行字母和单词的教学,可辅以字母课件进行教学,便于学生更好的领会和掌握。教师要注意侧重字母的书写教学,使学生养成正确的书写习惯。两个小游戏“Bingo”和“Listen and show”帮助学生在趣味活动中巩固了所学的全部字母。扩展性活动的设计目的在于复习本单元的单词。

人教版新课标PEP小学英语四年级上册My Schoolbag教案2篇
教师问:Can you spell these words? 如有学生能够拼出单词,教师要给与表扬并说:那让我们来看一看他拼的对不对,然后出示单词卡。如没有学生拼出单词,教师说:我们学习单词不仅要会说还要会写,今天我们就来学习几个单词的拼写,看谁学得快。然后出示单词卡。 让学生看单词卡拼读单词。 教师让学生看单词回答:How many letters in this word?学生回答后,让他们背着拼出单词。 教师让学生在四线三格中默写字母b, o, k, r, l, e, p, n, c, I, a,教师教学生在四线三格中书写单词。告诉学生首先要把每个字母书写正确,然后按照单词的拼写把字母写在一起,注意单词的每个字母间要有一点距离。教师在教写ruler和pencil-case时, 注意小写u和s还没有学习书写,让学生照着板书写就可以了。 让学生照板书抄字头,然后每个单词写一行。 (三)趣味操练(Practice)

高教版中职数学基础模块下册:8.4《圆》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 8.4 圆(二) *创设情境 兴趣导入 【知识回顾】 我们知道,平面内直线与圆的位置关系有三种(如图8-21): (1)相离:无交点; (2)相切:仅有一个交点; (3)相交:有两个交点. 并且知道,直线与圆的位置关系,可以由圆心到直线的距离d与半径r的关系来判别(如图8-22): (1):直线与圆相离; (2):直线与圆相切; (3):直线与圆相交. 介绍 讲解 说明 质疑 引导 分析 了解 思考 思考 带领 学生 分析 启发 学生思考 0 15*动脑思考 探索新知 【新知识】 设圆的标准方程为 , 则圆心C(a,b)到直线的距离为 . 比较d与r的大小,就可以判断直线与圆的位置关系. 讲解 说明 引领 分析 思考 理解 带领 学生 分析 30*巩固知识 典型例题 【知识巩固】 例6 判断下列各直线与圆的位置关系: ⑴直线, 圆; ⑵直线,圆. 解 ⑴ 由方程知,圆C的半径,圆心为. 圆心C到直线的距离为 , 由于,故直线与圆相交. ⑵ 将方程化成圆的标准方程,得 . 因此,圆心为,半径.圆心C到直线的距离为 , 即由于,所以直线与圆相交. 【想一想】 你是否可以找到判断直线与圆的位置关系的其他方法? *例7 过点作圆的切线,试求切线方程. 分析 求切线方程的关键是求出切线的斜率.可以利用原点到切线的距离等于半径的条件来确定. 解 设所求切线的斜率为,则切线方程为 , 即 . 圆的标准方程为 , 所以圆心,半径. 图8-23 圆心到切线的距离为 , 由于圆心到切线的距离与半径相等,所以 , 解得 . 故所求切线方程(如图8-23)为 , 即 或. 说明 例题7中所使用的方法是待定系数法,在利用代数方法研究几何问题中有着广泛的应用. 【想一想】 能否利用“切线垂直于过切点的半径”的几何性质求出切线方程? 说明 强调 引领 讲解 说明 引领 讲解 说明 观察 思考 主动 求解 思考 主动 求解 通过例题进一步领会 注意 观察 学生 是否 理解 知识 点 50

小学数学人教版五年级上册《解方程》说课稿
二、说教学目标知识与技能:初步理解“方程的解”和“解方程”的含义,以及之间的联系和区别。能用等式的性质解形如X±a=b的方程,掌握解方程的格式和写法。初步学会检验某个数是否是方程的解,培养学生检验的习惯,提高计算能力。过程和方法:通过探索、讨论、交流等活动,让学生初步理解“方程的解”和“解方程”的概念。经历运用等式的性质探究方程解法的过程,体会方程的解法和等式的性质之间的联系。情感、态度与价值观:1. 学生能积极参与数学学习活动,对数学有好奇心和求知欲。2. 在观察、猜想、验证等数学活动中,培养学生的数学素养。重点:方程的解和解方程的概念,初步掌握用等式性质来解简易方程的方法。难点:区别方程的解和解方程的含义。解方程的算理。三、说教法与学法教法:新课标指出,教师是学习的组织者、引导者、合作者,充分发挥学生的主体性。根据这一理念,我在教学中通过观察、猜想、验证等方式,自主探索、自主学习。有目的地运用知识迁移的规律,引导学生进行观察、比较、分析、概括,培养学生的逻辑思维能力。学法:①让学生学会以旧引新,掌握并运用知识迁移进行学习的方法;②让学生学会自主发现问题,分析问题,解决问题的方法。

小学数学人教版五年级上册解简易方程说课稿
一、 说教材1、教材内容:人教版小学数学第十册《解简易方程》及练习二十六1~5题。2、教材简析:本节课是在学生已经学过用字母表示数和数量关系,掌握了求未知数x的方法的基础上学习的。通过学习使学生理解方程的意义、方程的解和解方程等概念,掌握方程与等式之间的关系,掌握解方程的一般步骤,为今后学习列方程解应用题解决实际问题打下基础。3、教学目标:(1)使学生理解方程的意义、方程的解和解方程的概念,掌握方程与等式之间的关系。(2)掌握解方程的一般步骤,会解简单的方程,培养学生检验的习惯,提高计算能力。(3)结合教学,培养学生事实求是的学习态度,求真务实的科学精神,养成良好的学习习惯。渗透一一对应的数学思想。

小学数学人教版三年级上册《数字编码》说课稿
一、说教材(一)教材分析这部分教材是在新课标理念下新增加的一节实践活动课,重要是向学生渗透数字编码的数学思想。本节课是通过日常生活中的一些事例,如:学号、门牌号、身份证号等使学生进一步体会数字编码在日常生活中的应用,并通过实践活动进行简单的数字编码,培养学生的抽象、概括能力。(二)学生分析学生在第一学段已经对数字编码有了简单的了解,如:运动员的号牌、车牌号、邮编、门牌号等。学生也简单的知道数不仅可以用来表示数量和顺序,还可以用来编码。这节课就是在学生的生活经验和已有知识的基础上,进一步体会数字编码在日常生活中的应用,并通过实践活动进行简单的数字编码,培养学生的抽象、概括能力。(三)教学目标根据教材的特点和课标要求,从学生的实际出发,我确定了一下教学目标: 1、经历尝试编写本学校独一无二学号的过程,使学生体会数字编码在生活中的应用,探索数字编码的简单方法。 2.初步培养学生抽象概括的能力,提高应用意识和实践活动能力。 3.体会数字应用的广泛性,提高学习数学的兴趣和积极性。

小学数学人教版三年级上册《认识周长》说课稿
一、说课程标准《数学课程标准》中明确指出:应该从学生的生活经验和已有的知识出发,给学生呈现“现实的、有意义的、富有挑战性的”材料,提供充分的数学活动和交流的机会,引导他们在自主探索的过程中获得知识和技能,尽力实际问题抽象成数学模型并解释与应用的过程。二、教材及学情分析本节课是人教版3年级上册第七单元第2节内容,“认识周长”是“空间与图形”的重要内容之一。是在学生已经认识了长方形、正方形、三角形和圆形等平面图形的基础上进行教学的。教材先通过“森林运动会”——小蚂蚁围着树叶跑步,初步感知小蚂蚁的运动路线就是树叶的周长;然后对游泳池池口和篮球场周围边线进行观察,明确这条边线的长就是它们的周长,这里没有给出周长的定义,而是通过生活中这两个具体事例,让学生通过观察、操作,在获得直接感知的基础上认识周长的含义。接着以已有的直接经验为基础,让学生根据给定的图形去量一量、算一算,进一步理解周长,知道怎样可以测量并计算出周长。

小学数学人教版一年级上册《认识钟表》说课稿
一、教材分析《认识钟表》是义务教育课程标准实验教科书数学(人教版)一年级上册第七单元的教学内容。本节课要求学生对整时的认识,是学生建立时间观念的初次尝试,为以后“时、分”的教学奠定基础。二、学生分析一年级的学生由于年龄小,刚入学不久,好动、好奇、好玩。大部分学生在学前教育或家庭教育中多多少少都接受过一些关于时间的知识。一般来说,一名6岁的儿童每天起床、吃饭、上课、下课都要按照一定的时间来进行,这样在生活中潜移默化就感知到了时间这一抽象概念的存在。而且几乎每个家庭都有挂钟或手表,钟面、表面对于学生来说并不陌生。三、教学目标 1.初步认识钟面和电子表面,能结合自己的生活经验正确地读、写整时时刻,初步建立时间观念。 2.经历操作、讨论、交流等实践活动,进一步培养学生的动手、动口、动脑的实践应用能力和合作精神,发展数感。

小学数学人教版三年级上册《倍的认识》说课稿
一、说教材倍的认识是在学生认识和理解乘法意义的基础上学习的,学生将通过对已学习的有关乘法的知识进行迁移获得“倍”的概念。“倍”是一个新的概念,是一种数量之间的关系。通过对本内容的学习,初步建立倍的概念和简单的数学模型,有助于学生深入理解乘法的含义,拓宽应用乘法解决实际问题的范围与能力,培养数感,为今后学习分数、小数和百分数等相关知识奠定基础。二、说教学目标根据教材的特点和学生的实际情况,我预设目标如下:1、在充分感知的基础上,理解一个数是另一个数几倍的含义,初步建立倍的概念。2、通过动手操作,培养几何直观。3、使学生初步体会数学知识与日常生活的联系,培养学生观察、操作、分析及语言表达的能力,养成良好的学习习惯。三、说教学重难点:教学重点:理解一个数是另一个数几倍的含义,初步建立倍的概念。突破方法:通过反复的学具操作活动,让学生去观察、经历、体验和探索,在亲身感受中建立“倍”的概念。

小学数学人教版三年级上册《几分之几》说课稿
尊敬的各位评委老师、同仁们:大家好!今天我要进行说课的课题是《几分之几》。下面我对本课题主要从教材、教学目标、重难点、教法、学法、教学过程、板书设计等几方面进行简单分析。一、说教材(地位与作用)《几分之几》是人教版三年级第八单元第2个课时。在此之前,学生们已经学习了“几分之一”,这为过度到本课题的学习起到了铺垫的作用。而本课题的理论、知识等是学好分数的基础,它在整个分数的学习中起着承上启下的作用。二、说教学目标根据本教材的结构和内容,结合着三年级学生的认知结构及其心理特征,本节课我制定了以下三维教学目标:通过观察、猜测、比较、动手操作等合作参与数学学习活动,掌握分数表示的意义,感受数学与生活的密切联系,激发学习数学、探索数学的浓厚兴趣,使学生在数学活动中养成与人合作的良好习惯。从而掌握几分之几的读写和同分母的大小比较,理解分数各部分的名称及各部分表示的意义,初步培养有序地全面地思考问题的能力。

小学数学人教版一年级上册《6和7的组成》说课稿
一、说教材说课的内容是《义务教育课程标准实验教科书 数学》人教版一年级上册第五单元:《6—-10的认识和加减法》中的第二课时。这部分教材是为学生快速而正确进行6和7加减法计算做铺垫的内容。在这一阶段通过让学生初步经历从日常生活中抽象出数的过程,借助于生活中的实物和学生的操作活动进行教学,为学生了解数学的用处和体验数学学习的乐趣打下扎实的基础。基于以上认识,我确定本课的教学目标为:1.知识目标:通过动手摆学具教学使学生学会从实际生活中抽象出数,掌握6和7的组成。2.能力目标:培养学生观察、动手操作、口头表达的能力,渗透数学来源于生活,理解数学与日常生活的紧密联系,并运用于生活的辨证唯物主义思想。3.情感目标:通过探究活动,激发学生学习的热情,培养学生主动探究的能力。教材的重点、难点:本节课的重点是:掌握6、7的组成。本课难点是:‘6、7的组成’在实际中的灵活运用。

