-

2024年上半年工作总结和下半年工作计划汇编(6篇)
一、工作成效(一)全面统筹法治XX建设,以头雁之姿攻坚依法行政堵点痛点难点。一是纵深谋划顶层设计。全力筹划、组织召开县委全面依法治县委员会会议和办公室主任会议,对法治建设和“八五”普法中期考核评估工作进行安排部署。二是全域推开重点工作。部署开展道路交通安全和运输执法领域突出问题专项整治工作,公安、交通运输等部门通过自查自纠,共排整改问题108个。三是一体推进建设考评。6月对全县各乡镇、各部门(单位)法治建设重点工作推进落实情况进行专项督查,确保全县年度法治建设各项任务落实落细。四是依法行政深入推进。联合县委编办深入各乡镇就乡镇赋权事项进行调研评估,全面掌握乡镇赋权的落实情况。对全县27个行政执法单位的4265件执法案卷进行全面评查,达到了以评查促提升,以评查促规范的目的。审查县政府常务会议题41件。五是行政争议高效化解。

2024年上半年工作总结及2024下半年工作计划汇编(3篇)
7.加强高质量发展统计监测。一是强化经济监测预警。加强对上报数据进行横向、纵向的监测预警,同时对重点企业、重点行业的主要指标进行跟踪监测分析,撰写高质量统计分析文章,共撰写了各类经济形势分析及报告材料10余篇。二是撰写并发布了《XX区2022年国民经济和社会发展统计公报》,编印《XX统计月报》4册;编印了2021年《统计年鉴》。三是积极开展统计服务,为区委政研室、区政府经调室、区发改局、区财政局、区绩效办、区生态环境分局、区统战部等部门提供相关统计数据。8.扎实推进第五次全国经济普查工作。一是高度重视,部署早。4月,郑明明区长主持召开了五经普工作部署会议,研究明确了区五经普组织机构、方案制定、经费落实等重点工作,明确了全区五经普工作组织领导事项。6月,区委、区政府集中研究审核了相关工作方案文件。7月12日,全省、全市五经普动员会后,立即召开了全区五经普启动部署会议。

2024年上半年工作总结和下半年工作计划汇编(17篇)
一、工作完成情况(一)持续抓深抓实抓责任,汇聚力量促振兴。一是健全帮扶联系制度。建立统一高效的巩固拓展脱贫攻坚成果同乡村振兴有效衔接的议事协调工作机制,通过县巩固拓展脱贫攻坚成果专项小组研究部署重点工作,制发《XX县巩固拓展脱贫攻坚成果专项小组2024年工作要点》等系列文件。二是完善工作推进机制。每月印发《工作提示单》,不定期制发重点工作通报,加大调研走访力度,对重点工作做到常提醒、常督促,助推各镇、县直各单位落实主体责任。(二)持续抓巩固拓展脱贫攻坚成果,牢牢守好底线。一是推进三保一安联席制度。落实“三保一安”联席制度,在健全防止因病返贫致贫风险、控辍保学、农村脱贫人口住房安全动态监测、农村供水工程长效管理上下功夫,确保“三保障”和饮水安全成果巩固提升。截至目前,教育方面2024年享受春季学生资助241人约19.92万元,春季“雨露计划”97人14.7万元;医疗方面脱贫人口家庭医生总签约3663人,脱贫人口和监测对象已全部参加2024年医疗保险和防贫保;住房方面将3户脱贫户纳入危房改造计划,于10月底竣工并完成验收;饮水安全方面已启动城乡供水一体化项目,偏远地区新建4个饮水项目。

2023年人才工作总结及2024年工作打算材料汇编(4篇)
中心城区面积从不足x平方公里,到如今突破xx.x平方公里;交通建设从没有一米高等级公路,到如今构建起“铁公机”立体网络;农民人均纯收入从不足xxx元,到xxxx年底农村居民人均可支配收入飙升至xxxxx元翻开xx建地xx年的壮美画卷,沧桑巨变的背后离不开人才的付出、离不开人才的奉献。xx年筚路蓝缕的奋斗史,就是一部集聚人才、依靠人才、成就人才的发展史。——这是人才总量大幅跃增的xx年。从xxxx年每万人拥有人才不足xx人,到xxxx年每万人拥有人才xxx人,再到xxxx年每万人拥有人才xxxx人,增长近xx倍。——这是人才质量飞速提升的xx年。截至xxxx年底,全市大学以上学历人才占比由不足x%提高至xx%、增长xx余倍,一大批优秀人才获国家级荣誉表彰。——这是人才生态显著改善的xx年。从人才专项经费几乎为零,到人才工作投入近亿元;从人才缺乏基本住居保障,到拎包入住式人才公寓突破xxxx套;从没有专门的人才服务机构,到市县(区)全覆盖成立人才服务中心近悦远来的人才生态不断优化。

第二周国旗下讲话稿:发扬宏志精神,实现青春跨越
老师们,同学们,大家好!今天我国旗下讲话的题目是《发扬宏志精神,实现青春跨越》。XX年9月,宏志班在xx市xx实验中学创立了。从那时起到今天,历经三年时光,自强不息的田中人用青春和汗水换来了宏志大树的刚健与挺拔,铸就了xx中学今日的丰硕与芬芳。特别是XX年、XX年两年中考,宏志班的同学取得了优异的成绩,有90多名宏志生录取到四星级高中,圆满的完成了教育局下达的扬中、附中指标,这些数据不断刷新着田中教学质量的新高度,赢得了家长、社会的刮目相看和高度赞誉。喜人的成绩面前,我们追寻原因:到底是什么让田中学子不断书写美丽的传奇?我想:应该就是宏志精神。什么是宏志精神呢?宏志精神的核心就是“自强、勤奋、感恩”。《易经》中说:“天行健,君子以自强不息”。古往今来,成就大事之人,都是自强之人。勾践卧薪尝胆,实现了“三千越军可吞吴”的壮举;祖逖闻鸡起舞,赢得了东晋军事家的美名;曹雪芹披阅十载,增删五次,铸就了《红楼梦》的绝世经典。人生的道路漫长而又精彩:我们要学会在阳光中欢笑,在阴霾中坚强,在狂风中抓紧希望,在暴雨中坚守理想;自强不息,乐观向上,走出一条属于自己的人生之路。

第十二周国旗下讲话稿:冬季长跑,让健康与我同行
第十二周国旗下讲话:冬季长跑,让健康与我同行尊敬的老师、亲爱的同学们:大家好!我是高一15班的雷xx。今天我国旗下讲话的题目是:冬季长跑,让健康与我同行。在这个金桔飘香的季节里,同学们,你们是否听见了冬天的脚步在向我们临近?随着冬天的到来,皮肤干燥、饮食减少、伤风感冒等各种疾病也随之而来。我想从此时开始,我们全校师生应该树立起“健康第一”的观念,享受阳光下美好的时光,利用好这些时间积极投身体育活动,强健我们的体魄。为此,我对深入持久的开展阳光体育冬季长跑提出以下几点希望:一、在活动中加强“诚信”的自我教育,提高自我锻炼意识和参与意识,促进学校体育活动健康积极发展。二、条件受限形式可变,长跑并非是唯一的锻炼方式,同学们要结合实际情况,开展形式多样的体育活动,关键在于运动。

春季学期第二周国旗下讲话稿:争做文明学生,共筑美好校园
老师们,同学们,大家早上好!今天我国旗下讲话的主题是:争做文明学生,共筑美好校园。大家知道做什么事情不简单、做什么事情不平凡吗?把每一件简单的事情做好,就是不简单;把每一件平凡的事情做好,就是不平凡。我的一个好朋友,每次在食堂吃完饭,都会一边把盘子递给收餐具的阿姨,一边礼貌地对她说声“谢谢”。收餐具的阿姨通常忙得顾不上回答——她们正以最快的速度整理着几只手同时甩在桌上的餐盘。不过也有时候,阿姨会冲我们笑笑,或者开心地说“不用谢”,然后继续麻利地工作。我不知道这一句简单的“谢谢”能有多大的作用,不过我想,至少这个阿姨的一天可以因此多一丝愉快,我们的校园里可以多一点文明的正能量。

XX镇中心初级中学2023—2024学年度第二学期工作总结
五、总务后勤工作方面在本学期的教育教学工作中,总务工作在工作中坚持发挥后盾保障作用,本着以教书育人,服务育人,服务教学的原则,坚持履行学校的整体工作步骤,切实完成好学校的总务后勤工作。1.在后勤服务工作中,本着服务教学的意识,着力强化后勤队伍建设,努力增强服务意识。2.严格履行财务制度,规范财务行为。在经费使用方面执行预算审批制度,在购物方面实行采购审批和政府采购制度,杜绝了各种不正之风,保证了资金的效益最大化。3.学校和各班班主任签定了班班通责任书,加强了班班通设备管理。同时制定了《班级财产管理制度》,把公物管理列入班主任考核内容之一,加强了财产管理。

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
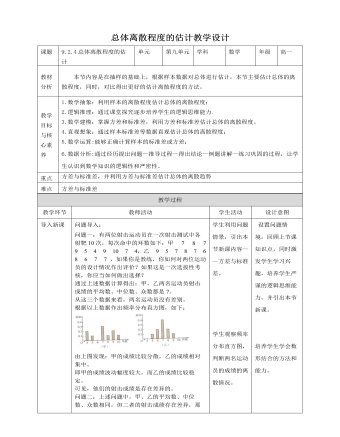
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
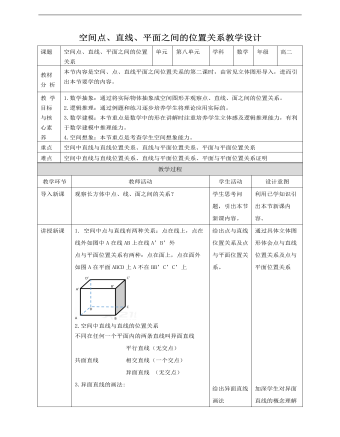
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
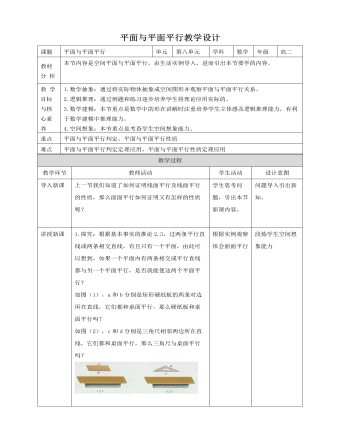
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
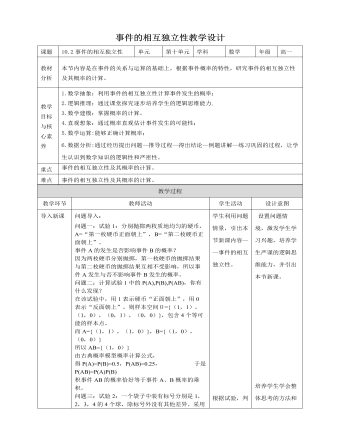
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
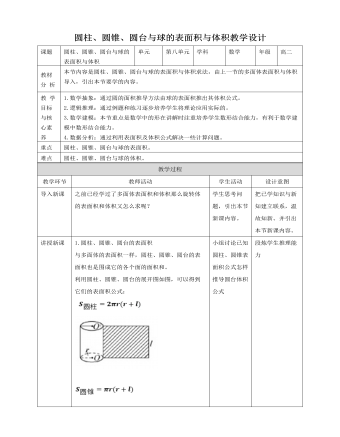
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
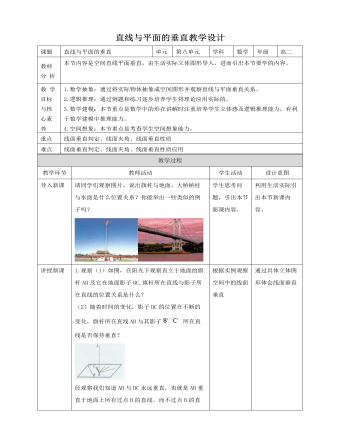
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
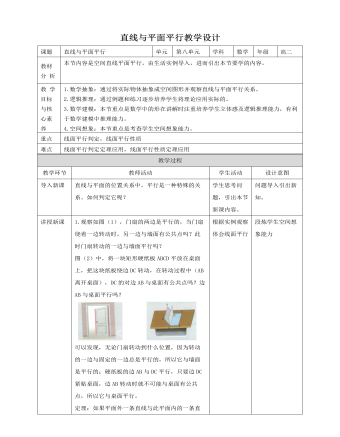
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=
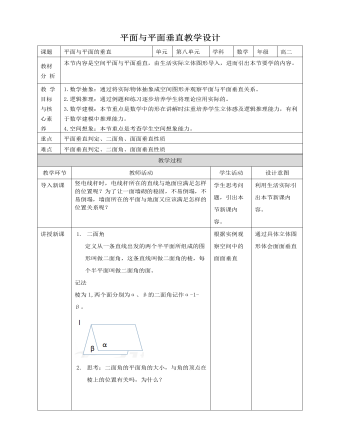
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?






