-

人教版高中地理必修2人口的空间变化教案
影响我国古代人口大规模迁移的因素,与影响我国近几十年人口迁移的因素有何不同?(古代:战乱,其次为开疆拓土、流放、戍边等。现代:国家政策、社会变革、经济发展、个人需求等。)2、为什么有这样的不同?(古代人口迁移受统治者及其行政力量的束缚。由于自给自足的经济十分脆弱,加之频繁的战争以及自然灾害等影响,人民难以安居乐业,不得不背井离乡大批迁移。近几十年来随着社会经济的发展、贸易的往来和交通的便捷,我国人口迁移不仅数量增加,而且频率加快,使各地人们的交往更加密切。)教师总结:从古今中外的人口迁移现象中,我们可以看出在人类历史早期人口迁移中重要的因素是什么?(自然因素)现在什么因素起重要作用?(经济因素)。但是在某种特定的时空条件下,任何一种因素都有可能成为促使人口迁移的决定性因素。【作业设计】查阅49年以来中国历年的人口数据资料,绘制人口增长的统计图表,探究中国人口增长的发展趋势

人教版高中地理必修3荒漠化的防治教案
1.萨赫勒地区位于撤哈拉沙漠的南缘。请根据下面的图文资料,并联系已学知识,分析萨赫勒地区的气候等自然特征,并说明荒漠化的潜在自然因素。点拨:资料表明萨林勒地区正处于干旱与半干旱、热带沙漠与热带草原的过渡地带;津德尔是其中有代表性的居民点,其月均温都在22℃以上,甚至达到33℃,可想而知其蒸发量是巨大的。在降水方面,这里的年降水量不足500毫米,且基本集中在夏季,特别是7、8两个月。以其有限的而且特别集中的降水状况与其全年的高温、高蒸发量相比,确实是个容易产生环境问题的敏感地区。客观上,这里就潜在着荒漠化的自然因素,这是本地区的地理位置和当地的水热条件所决定的。2.气候的严酷性决定了萨赫勒地区的传统经济以自给性质的游牧业为主。20世纪以来,随着沿岸国家人口和经济的发展及本区交通条件的改善,这里的传统游牧经济向商品性的定居牧业经济转化。
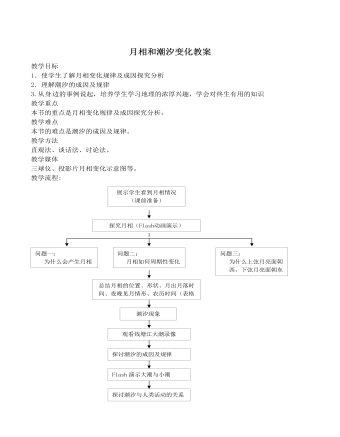
人教版高中地理选修1月相和潮汐变化教案
5.对土星五号火箭和登月舱的质疑现代航天飞机只能把20吨载荷送上低轨,而当 年的土星五号却能轻而易举地把100吨以上载荷送上地球轨道,将几十吨物体推出地球重力圈,为什么后来却弃而不用,据说连图纸都没有保存下来?6.温度对摄影器材的影响月面白天可达到121°C,据图片看,相机是露在宇航服外而没有采用保温措施的。胶卷在66°C就会受热卷曲失效,怎么拍得了照片?这些人士认为,对以上这一切美国政府一直没个 交代,而知情者由于担心生活和安全受到影响,甚至可能直接遭到了胁迫,至今对此沉默不言。但相信不久的将来,诞生于美苏太空竞赛年代的“登月骗局”定会水落石出。反驳不过,也有许多人认为“阿波罗”登月计划不可能造假:首先因为该计划当时是在全球实况转播的,近亿人亲眼看到。另外,宇航员还从月球带回了一些实物,如岩石。
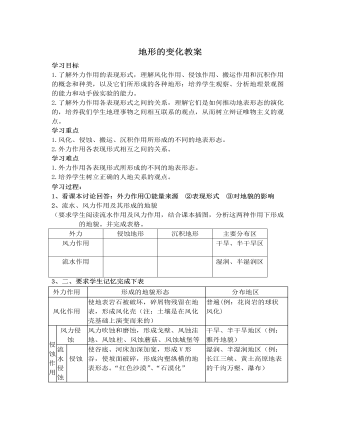
人教版高中地理选修1地形的变化教案
学习目标1.了解外力作用的表现形式,理解风化作用、侵蚀作用、搬运作用和沉积作用的概念和种类,以及它们所形成的各种地形;培养学生观察、分析地理景观图的能力和动手做实验的能力。2.了解外力作用各表现形式之间的关系,理解它们是如何推动地表形态的演化的,培养我们学生地理事物之间相互联系的观点,从而树立辩证唯物主义的观点。学习重点1.风化、侵蚀、搬运、沉积作用所形成的不同的地表形态。2.外力作用各表现形式相互之间的关系。学习难点1.外力作用各表现形式所形成的不同的地表形态。2.培养学生树立正确的人地关系的观点。学习过程:1、看课本讨论回答:外力作用①能量来源 ②表现形式 ③对地貌的影响2、流水、风力作用及其形成的地貌

人教版高中地理选修2荒漠化的成因与防治教案
1、图4.10“西北地区土地荒漠化的人为因素(以风力作用为例)图”产生荒漠化的人为因素有过度农垦、过度放牧、过度樵采和不合理利用水资源等。从荒漠化和人类的关系来看,荒漠化的发生、发展和社会经济有着密切的联系,人类不合理的经济活动不仅是荒漠化发生的主要原因和活跃因素,同时人类又是它的直接受害者。2、图4.14“荒漠植物的生态适应图”荒漠植物的生态适应特征表现在:a类为肉质植物,体内薄壁组织可储存大量水分,其近地表分布的根系可以在偶然而短暂的降水过程(如暴雨)中收集水分;b类植物一方面利用其近地表根系吸收可能的降水,另一方面根系向纵深发展,以利用稳定的地下水;c类为微叶或无叶型植物,叶片强烈缩小或退化,由绿色叶茎行使光合作用功能,蒸腾很弱。【教学内容】一、荒漠化的成因1.荒漠化的自然原因荒漠化的自然原因包括干旱(基本条件)、地表物质松散(物质基础)和大风吹扬(动力因素)。

国企公司加强廉洁文化建设经验做法总结
当前,国企改革进入了全面提速阶段,xx秉承机构精简、人员精干的“扁平化”原则,采用机关职能管理+现场组织实施管辖+生产属地委托+市场化专业技术支撑服务的模式高效运转。实现协同效应最大化、资源利用高效化、生产经营数字化和企业管理规范化,人均完成的选商、物资采购、合同的签订、结算、面对的技术服务商,要比非油公司更多更复杂。在面临繁重的生产建设任务的同时,必将面临形形色色的利益诱惑和廉洁考验。因此,要聚焦廉洁风险,探索培育廉洁文化,推动廉洁文化外溢输出,将其价值理念、行为规范和制度规范“内化于心、外化于行”,提升管理人员、承包商廉洁从业意识。一、以企业文化为抓手,厚植廉洁文化理念“油公司”模式下,市场化程度高,用工方式多样化,企业业务支撑人员较多,员工的经营理念、管理经验、文化积淀不同,对廉洁文化的认识还不够深入。

【高教版】中职数学基础模块上册:5.3任意角的正弦函数、余弦函数和正切函数
【教学目标】知识目标:⑴ 理解任意角的三角函数的定义及定义域;⑵ 理解三角函数在各象限的正负号;⑶掌握界限角的三角函数值.能力目标:⑴会利用定义求任意角的三角函数值;⑵会判断任意角三角函数的正负号;⑶培养学生的观察能力.【教学重点】⑴ 任意角的三角函数的概念;⑵ 三角函数在各象限的符号;⑶特殊角的三角函数值.【教学难点】任意角的三角函数值符号的确定.【教学设计】(1)在知识回顾中推广得到新知识;(2)数形结合探求三角函数的定义域;(3)利用定义认识各象限角三角函数的正负号;(4)数形结合认识界限角的三角函数值;(5)问题引领,师生互动.在问题的思考和交流中,提升能力.
小学数学苏教版六年级下册《第六单元第三课反比例关系、反比例量》教学设计说课稿
提问:1.怎样判断两种相关联的量是否成正比例?用字母怎样表示正比例关系? 2.判断下面两种量是否成正比例?为什么? (1)时间一定,行驶的路程和速度 (2)除数一定,被除数和商 3.单价、数量和总价之间有怎样的关系?在什么条件下,两种量成正比例? 4.导入新课: 如果总价一定,单价和数量的变化有什么规律?这两种量存在什么关系?今天,我们就来研究这种变化规律。

小学数学人教版六年级下册《第五课图形的认识与测量(第2课时)》教案说课稿
【课时安排】 1课时【教学过程】1.回顾梳理、归纳总结。师:我们学过哪些立体图形?生:长方体、正方体、圆柱体、圆锥体师:它们分别有哪些特征?师生共同总结立体图形的特征。 课件演示:长方体的特征:6个面是长方形(特殊情况有两个对面是正方形)相对的面完全相同;12条棱,相对的4条棱长度相等;8个顶点。正方体的特征:6个面都相等,都是正方形;12条棱都相等;8个顶点。圆柱的特征:上下两个面是完全相同的圆形,侧面是一个曲面,沿高展开一般是个长方形。上下一样粗;有无数条高,每条高长度都相等。

小学数学人教版六年级下册《第五课图形的认识与测量(第1课时)》教案说课稿
2.三角形的分类。师:你能给三角形按照不同的标准进行分类吗?生用自己喜欢的方式整理分类,然后汇报:生:三角形按角分为锐角三角形、直角三角形、钝角三角形。师:什么是锐角三角形、直角三角形、钝角三角形?生:三个角都是锐角的三角形叫做锐角三角形;有一个角是直角的三角形叫做直角三角形;有一个角是钝角的三角形叫做钝角三角形。生:三角形按边分为不等边三角形(三条边都不相等)、等腰三角形(等边三角形) 等腰三角形的两条边相等,等边三角形的三条边都相等。3.四边形分类。师:你能给四边形分类吗?生:四边形分为平行四边形和梯形;平行四边形包括长方形和正方形,长方形又包括正方形;梯形包括等腰梯形和直角梯形。4.直线、射线和线段的关系。小组内互相交流,然后汇报:

高教版中职数学基础模块下册:7.1《平面向量的概念及线性运算》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 7.1 平面向量的概念及线性运算 *创设情境 兴趣导入 如图7-1所示,用100N①的力,按照不同的方向拉一辆车,效果一样吗? 图7-1 介绍 播放 课件 引导 分析 了解 观看 课件 思考 自我 分析 从实例出发使学生自然的走向知识点 0 3*动脑思考 探索新知 【新知识】 在数学与物理学中,有两种量.只有大小,没有方向的量叫做数量(标量),例如质量、时间、温度、面积、密度等.既有大小,又有方向的量叫做向量(矢量),例如力、速度、位移等. 我们经常用箭头来表示方向,带有方向的线段叫做有向线段.通常使用有向线段来表示向量.线段箭头的指向表示向量的方向,线段的长度表示向量的大小.如图7-2所示,有向线段的起点叫做平面向量的起点,有向线段的终点叫做平面向量的终点.以A为起点,B为终点的向量记作.也可以使用小写英文字母,印刷用黑体表示,记作a;手写时应在字母上面加箭头,记作. 图7-2 平面内的有向线段表示的向量称为平面向量. 向量的大小叫做向量的模.向量a, 的模依次记作,. 模为零的向量叫做零向量.记作0,零向量的方向是不确定的. 模为1的向量叫做单位向量. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 带领 学生 分析 引导 式启 发学 生得 出结 果 10

高教版中职数学基础模块下册:7.1《平面向量的概念及线性运算》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 7.1 平面向量的概念及线性运算 *创设情境 兴趣导入 如图7-1所示,用100N①的力,按照不同的方向拉一辆车,效果一样吗? 图7-1 介绍 播放 课件 引导 分析 了解 观看 课件 思考 自我 分析 从实例出发使学生自然的走向知识点 0 3*动脑思考 探索新知 【新知识】 在数学与物理学中,有两种量.只有大小,没有方向的量叫做数量(标量),例如质量、时间、温度、面积、密度等.既有大小,又有方向的量叫做向量(矢量),例如力、速度、位移等. 我们经常用箭头来表示方向,带有方向的线段叫做有向线段.通常使用有向线段来表示向量.线段箭头的指向表示向量的方向,线段的长度表示向量的大小.如图7-2所示,有向线段的起点叫做平面向量的起点,有向线段的终点叫做平面向量的终点.以A为起点,B为终点的向量记作.也可以使用小写英文字母,印刷用黑体表示,记作a;手写时应在字母上面加箭头,记作. 图7-2 平面内的有向线段表示的向量称为平面向量. 向量的大小叫做向量的模.向量a, 的模依次记作,. 模为零的向量叫做零向量.记作0,零向量的方向是不确定的. 模为1的向量叫做单位向量. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 带领 学生 分析 引导 式启 发学 生得 出结 果 10

空间向量及其运算的坐标表示教学设计人教A版高中数学选择性必修第一册
一、情境导学我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.二、探究新知一、空间直角坐标系与坐标表示1.空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.

用空间向量研究距离、夹角问题(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、点到直线的距离、两条平行直线之间的距离1.点到直线的距离已知直线l的单位方向向量为μ,A是直线l上的定点,P是直线l外一点.设(AP) ?=a,则向量(AP) ?在直线l上的投影向量(AQ) ?=(a·μ)μ.点P到直线l的距离为PQ=√(a^2 "-(" a"·" μ")" ^2 ).2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.点睛:点到直线的距离,即点到直线的垂线段的长度,由于直线与直线外一点确定一个平面,所以空间点到直线的距离问题可转化为空间某一个平面内点到直线的距离问题.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 . 答案: √174/6解析:如图,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),E(0,2,1),F(1,0,2),(EF) ?=(1,-2,1),

用空间向量研究直线、平面的位置关系(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、空间中点、直线和平面的向量表示1.点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量(OP) ?来表示.我们把向量(OP) ?称为点P的位置向量.如图.2.空间直线的向量表示式如图①,a是直线l的方向向量,在直线l上取(AB) ?=a,设P是直线l上的任意一点,则点P在直线l上的充要条件是存在实数t,使得(AP) ?=ta,即(AP) ?=t(AB) ?.如图②,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使(OP) ?=(OA) ?+ta, ①或(OP) ?=(OA) ?+t(AB) ?. ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.1.下列说法中正确的是( )A.直线的方向向量是唯一的B.与一个平面的法向量共线的非零向量都是该平面的法向量C.直线的方向向量有两个D.平面的法向量是唯一的答案:B 解析:由平面法向量的定义可知,B项正确.

用空间向量研究直线、平面的位置关系(2)教学设计人教A版高中数学选择性必修第一册
跟踪训练1在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC;(2)BD1⊥EB1.(2)∵(BD_1 ) ?=(-1,-1,1),(EB_1 ) ?=(1/2 "," 1/2 "," 1),∴(BD_1 ) ?·(EB_1 ) ?=(-1)×1/2+(-1)×1/2+1×1=0,∴(BD_1 ) ?⊥(EB_1 ) ?,∴BD1⊥EB1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E(1/2 "," 1/2 "," 0),B1(1,1,1).(1)∵(BD_1 ) ?=(-1,-1,1),(AC) ?=(-1,1,0),∴(BD_1 ) ?·(AC) ?=(-1)×(-1)+(-1)×1+1×0=0.∴(BD_1 ) ?⊥(AC) ?,∴BD1⊥AC.例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.思路分析一种思路是不建系,利用基向量法证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直,从而根据线面垂直的判定定理证得结论;另一种思路是建立空间直角坐标系,通过坐标运算证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直;还可以在建系的前提下,求得平面EFB1的法向量,然后说明(D_1 M) ?与法向量共线,从而证得结论.证明:(方法1)因为E,F,M分别为棱AB,BC,B1B的中点,所以(D_1 M) ?=(D_1 B_1 ) ?+(B_1 M) ?=(DA) ?+(DC) ?+1/2 (B_1 B) ?,而(B_1 E) ?=(B_1 B) ?+(BE) ?=(B_1 B) ?-1/2 (DC) ?,于是(D_1 M) ?·(B_1 E) ?=((DA) ?+(DC) ?+1/2 (B_1 B) ?)·((B_1 B) ?-1/2 (DC) ?)=0-0+0-1/2+1/2-1/4×0=0,因此(D_1 M) ?⊥(B_1 E) ?.同理(D_1 M) ?⊥(B_1 F) ?,又因为(B_1 E) ?,(B_1 F) ?不共线,因此D1M⊥平面EFB1.

北师大版初中七年级数学下册用关系式表示的变量间关系说课稿2篇
一.说教材我今天说课的内容是义务教育课程标准北师大版七年级下册第四单元第二节的《用关系式表示的变量间关系》。在上节课的学习中学生已通过分析表格中的数据,感受到变量之间的相依关系,并用自己的语言加以描述,初步具有了有条理的思考和表达的能力,为本节的深入学习奠定了基础。二.说教学目标本节课根据新的教学理念和学生需要掌握的知识,确立本节课的三种教学目标:知识与能力目标:根据具体情况,能用适当的函数表示方法刻画简单实际问题中变量之间的关系,能确定简单实际问题中函数自变量的取值范围,并会求函数值。过程与方法目标:经历探索某些图形中变量之间的关系的过程,进一步体会一个变量对另一个变量的影响,发展符号感。情感态度与价值观目标:通过研究,学习培养抽象思维能力和概括能力,通过对自变量和因变量关系的表达,培养数学建模能力,增强应用意识。

冲刺四季度表态发言
1、要学习他们思想解放,干事创业的大气魄,深化抢抓机遇的发展意识。同样处于宏观调控的背景,同样面临土地、资金、人才等要素的制约,同样面对竞相发展的态势,兄弟乡镇千方百计解难题,百折不挠抓推进,变挑战为机遇,化被动为主动,牢牢掌握了发展的主动权。他们在产业布局上的大思路,在项目建设上的大推进,在关注民生上的大投入,在园区建设上的大手笔,无不让我们感到震撼。西湖镇今年上半年地区生产总值达24亿元,固定资产投资预计达32亿元,增幅达20%以上。在标兵越跑越远,追兵越追越近的形势下,我们不仅要看到有形的差距,更要看到无形的差距,差距在思想解放的程度上、破解难题的力度上、抢抓机遇的能力上、发展理念的突破上

2024年度乡宣传年中总结
三是移风易俗方面,目前部分村仍存在相互攀比礼金金额、“要面子不要里子”等问题,增加了农民群众的经济负担;部分村红白理事会存在流于形式、工作开展不够规范、相关制度不够明晰等问题。四是文明创建方面,一是认识上还不够统一。少数同志认为,文明创建不是自己分管的事,对安排的网格管理和包保责任态度不积极,不能做好安排、亲自过问、亲自督查、亲自问效。二是集镇建管水平还亟待提升,返潮现象严重。培育和践行社会主义核心价值观的宣传氛围还需浓郁;沿街商住户“门前三包”责任制度还没有落实,占道经营、店外经营、乱泼乱倒现象仍存在,乱搭乱建、乱摆乱放、乱拉乱晾还较严重;车辆乱停放,特别是占道停车现象突出。三、下一步工作计划(一)持续推进新时代文明实践(所)站建设。

初中法制安全教育教案
一.生活中有哪些意外 1.生活当中有哪些意外情况,或者在哪些方面,我们要注意安全?A(个别+补充回答) 比如有:火灾、用电安全、煤气中毒、交通事故、突发病症,遇见被偷被抢等等。 2.遇见这些紧急情况我们能不能慌张?A应该怎样才对?B为什么?C 不要慌张,在情绪上要镇定,因为越是慌张,对事情的处理其实越不利。

