-

狼牙山五壮士教案 3篇
二、教学目标 1、知识目标:了解狼牙山五壮士英勇战斗,坚贞不屈,壮烈牺牲的英雄事迹。 2、能力目标:理解能力、朗读体会能力的培养。 3、德育目标;学习他们爱护群众,英勇杀敌,为了祖国和人民的利益勇于献身的崇高精神。

《重整河山待后生》教案
教学过程:一、导入:首先导入一段相声表演的视频,那么,相声是一种大家都非常喜闻乐见的一种说唱音乐的艺术表演形式,本单元我们就来了解一下我国的说唱音乐。那么,接下来就来介绍一下说唱音乐这种艺术表演形式。说唱音乐又称曲艺音乐,那么,在曲艺中除少数曲种外,大多数以说唱结合为其特点,唱居主要地位。说唱音乐在南方的代表——弹词(苏州评弹),在北方的代表——鼓词(京韵大鼓)。二、对比欣赏传统京韵大鼓与《重整河山待后生》。首先播放一段传统京韵大鼓唱段和《重整河山待后生》,找出二者之间的区别。思考:(1)音乐的特点:《重整河山待后生》是电视连续剧《四世同堂》主题歌,其旋律是采用京韵大鼓的音调素材写成的。它通过众多的、形形色色的人物之间错综复杂的关系,展现了抗战八年来沦陷区广大人民血与泪交织的生活画面,揭露了日本侵略者血腥统治、汉奸的卑鄙下流的嘴脸,描述了中国人民所遭受的民族灾难,反映了在这一历史时期人民大众逐渐觉醒的过程和顽强不屈、奋起抗日的精神。(2)情感的体现:《重整河山待后生》这个唱段,表现了抗日战争时期沦陷区人民的苦难,歌颂了中国人民为雪国耻不怕流血牺牲、大义凛然、坚强不屈的民族精神。艺术家骆玉笙在演唱时,发挥了她音域宽阔、抒情色彩浓郁的演唱风格,并揉进了悲壮苍凉的演唱特点。强化了悲壮的、大义凛然、坚强不屈的音乐情绪。

欣赏《梁山伯与祝英台》教案
一、导入(回忆式) “一个千古传颂的故事,一段柔美、深情地旋律,打动了多少爱乐人的心。小提琴协奏曲《梁山伯与祝英台》,就是这样一首令欣赏者为之倾倒的我国优秀的音乐作品之一。今天就让我们共同欣赏这首小提琴协奏曲《梁山伯与祝英台》。二、作品创作背景简析这是一部以广泛流传的民间故事《梁山伯与祝英台》为题材,以越剧音乐为素材而写成的单乐章小提琴协奏曲。如今已列入世界名曲,Butterfly-loves(《蝴蝶的爱情》)。作品中的两位主人公梁山伯与祝英台,在历史上是否真有这两个人物呢?(讨论。)这一民间传说与史实有很大的出入。梁祝二人可谓是千年等一回。据史册记载,梁山伯是明朝的一个县官,因秉公办案,有“梁青天”的美称。梁山伯死后,人们为了纪念他,把他葬在山清水秀的胡桥镇。可是在挖掘墓地时,发现一墓穴,穴中有一块刻着“祝英台女侠之墓”的石碑。石碑背面记载着祝英台的身世:“祝英台乃是南北朝时代的陈国人,一生行侠仗义,后来遭贪官马文才父子陷害致死,当地人们偷偷将其安葬于胡桥镇。由于梁祝二人都是为百姓办好事的人,人们便把他俩合葬在一起。从那以后,在民间就产生了各种各样关于梁祝感人至深的故事。三、乐曲的结构采用了欧洲古典传统的奏鸣曲式,下面依结构图欣赏作品。引子:乐曲一开始由长笛奏出了华彩的旋律,呈现出一派春光明媚、鸟语花香的景象。由双簧管奏出的主题音调,取自越剧的过门音乐。呈示部:主部主题──在竖琴的伴奏下,小提琴演绎出纯朴而美丽的“爱情主题。”(这段旋律在整部作品中起到了举足轻重的作用。多少人听了段旋律都为之陶醉。作者在选取这段主题时可是费了一番苦心。当年他们还是上海音乐学院作曲系的学生。何占豪曾在杭州越剧团当演员,他对越剧音乐既熟悉又喜爱。在创作《梁祝》时,故事流传在浙江一带,越剧是浙江的代表剧种,他决心从越剧音乐中取材。据平时的观察,许多越剧名演员,不论他们演出任何剧目,只要唱到一段唱腔时,台下都会博得热烈地掌声为之呼应。作者抓住了这段唱腔作为《梁祝》中“爱情主题”的基本音调。这段主题是全曲的核心的音调。)

欣赏《梁山伯与祝英台》教案
教学过程:一、组织教学:播放动画片《梁祝》的flash动画, 让学生初次感受主 题音乐。二、新课教学:1、导入新课:教师设问:同学们你们听过这个动画短片的音乐吗?谁知道这段音乐叫什么名字?(学生回答。) 教师设问:有谁了解《梁祝》这个民间故事?试着给大家讲述一下。(学生回答。) 今天,我们就一起来欣赏这首被列入世界名曲,又被称作butterfly—lovers(蝴蝶的爱情)小提琴协奏曲《梁山伯与祝英台》。设计目的:激发学生的兴趣,引导学生去欣赏乐曲。2、相关知识:(教师讲授,出示多媒体课件。)(1)教师简介《梁祝》在世界上的影响及地位:小提琴协奏曲《梁祝》被中国听众被誉为“我们的交响音乐”。外国听众也认为乐曲是一部“非常迷人和神奇的音乐”,“最美妙的旋律”。(2)曲作者简介: 何占豪:作曲家,浙江人。主要作品:小提琴齐奏曲《姊妹歌》,弦乐四重奏《过节》,交响乐《刘胡兰》、越剧《孔雀东南飞》配乐。陈钢:作曲家,上海市人。主要作品:《阳光照耀着塔什库尔干》。(3)知识点的讲解: 协奏曲:独奏乐器和管弦乐器协同演奏的大型器乐套曲,它是充分发挥某种独奏乐器演奏技巧和鲜明个性的音乐作品意大利原文是“竞奏”。3、下面,欣赏《梁祝》的主要部分音乐。

欣赏《梁山伯与祝英台》教案
教学过程第一环节:恋蝶——欣赏越剧《十八相送》感受越剧韵味,了解越剧。 1、提问导入特点,并为欣赏下一作品做好铺垫。(1)越剧是浙江地方戏剧剧种之一,你能说出一些著名的越剧代表作品吗?(2)导出越剧《梁祝》并请学生说说梁祝故事。(3)教师小结。(4)欣赏越剧《十八相送》。(5)简单介绍越剧特点(唱腔、语言)。第二环节:颂碟——欣赏小提琴协奏曲《梁祝》片断。1、导入:介绍作品地相关知识。(1)教师:这个千古传颂的爱情故事可以用越剧的形式来表现。那么,我们是否可以用其他形式来表现呢?我们中国就有两位作曲家何占豪和陈刚,他们为了探索交响音乐的民族化,选择了这一家喻户晓的民间传说为题材,吸取越剧中的曲调为素材,运用西洋手法,成功地创作了一部小提琴协奏曲《梁祝》。(2)介绍乐器小提琴、大提琴(出示图片)。 2、欣赏“爱情主题”(1)请学生聆听爱情主题音乐根据提问,让学生思考:①这段主旋律由哪样乐器演奏? ②这段主旋律有什么特点?自主参与讨论分析作品。(2)学生思考并回答。(3)教师总结: 旋律优美动听、委婉曲折,带有越剧韵味。节奏舒缓,情绪明朗。表现出爱情的美好。3、介绍协奏曲 协奏曲是指一种由独奏乐器与管弦乐队协同演奏的大型器乐作品。在音乐 进行中,独奏乐器与乐队常常轮流出现,独奏时乐队处于伴奏地位。全奏时,独奏乐器休止,完全由乐队演奏。

大班体育教案:花果山之战
⒉设各种难度场景,引导幼儿大胆地面对困难、主动挑战困难、创造性地战胜困难,尽情体验胜利的喜悦。二、活动准备:⒈活动材料:桌子18张、桃子(纸球)若干个、录音机等。⒉活动环境布置:⑴三列由桌子并成的石洞。⑵三列由桌子并成、相隔的石桥。⑶将桌子搭成高(130厘米)的“花果山”。⑷教师扮演—孙悟空、妖怪。

中班体育教案:登山
准备 1.手绢人手一条,“梅花桩”若干(梅花桩用5个易拉罐灌沙后捆扎在一起,固定好)。旗杆两根。 2.场地布置如下图。 玩法 1.将幼儿分成人数相等的两队,分别列队站在起跑线后。

XX公司财务资产部2024年上半年总结及下半年计划
三是清理处置“两非”“两资”,积极助力提质增效。认真落实集团公司关于加快清理非优势业务和低效无效资产的工作部署,组织集团各所属企业深入开展调查摸底,分门别类建立台账,逐笔逐项明确处置目标、处置责任、处置流程、处置思路和措施,本着先易后难的原则,分批分类推进“两非”“两资”处置工作,力争年内取得明显进展。同时,探索建立清理处置低效无效资产的工作机制,包括汇报沟通机制、集体研判机制、督导检查机制、动态销号机制,以高效机制推动低效无效资产逐步出清、确保资产质量稳步提升。四是抓紧开展“两金”压降,推动提升经济效益。对照年度经营目标责任书确定的考核目标,聚焦应收账款和存货两大领域,统筹运用市场、信用、法治等手段,一体推进旧欠清收和“两金压控”两项重点,全面清理处置应收账款、其他应收款、预付账款、存货,进一步盘活资产、回笼资金,降低财务风险,提高资产质量,增加经济效益,并着眼集团长远高质量发展,全面梳理自查制度、机制、流程等方面的短板和不足,建立健全压控“两金”的长效机制,持续提升造血能力,推动全集团持续稳健高质量发展。

公司财务资产部2024年上半年总结及下半年计划
三是清理处置“两非”“两资”,积极助力提质增效。认真落实集团公司关于加快清理非优势业务和低效无效资产的工作部署,组织集团各所属企业深入开展调查摸底,分门别类建立台账,逐笔逐项明确处置目标、处置责任、处置流程、处置思路和措施,本着先易后难的原则,分批分类推进“两非”“两资”处置工作,力争年内取得明显进展。同时,探索建立清理处置低效无效资产的工作机制,包括汇报沟通机制、集体研判机制、督导检查机制、动态销号机制,以高效机制推动低效无效资产逐步出清、确保资产质量稳步提升。四是抓紧开展“两金”压降,推动提升经济效益。对照年度经营目标责任书确定的考核目标,聚焦应收账款和存货两大领域,统筹运用市场、信用、法治等手段,一体推进旧欠清收和“两金压控”两项重点,全面清理处置应收账款、其他应收款、预付账款、存货,进一步盘活资产、回笼资金,降低财务风险,提高资产质量,增加经济效益,并着眼集团长远高质量发展,全面梳理自查制度、机制、流程等方面的短板和不足,建立健全压控“两金”的长效机制,持续提升造血能力,推动全集团持续稳健高质量发展。

综合部2024年上半年工作总结及下半年工作计划
五是基层减负减压不松劲。坚持少开会、开短会、发短文、讲短话、简办事,注重提升会议与公文质量和效果,提振干部精神风貌、纪律意识和工作作风,提高行政效率。修订公司会议管理办法,每周五统筹合理安排公司周会议计划,采取合并、套开的方式严格压缩会议数量和时间;充分利用现代通信和技术手段召开视频会议,避免层层开会现象;下发严肃会议纪律、规范视频会议通知,严肃会风会纪。三、存在的主要问题及解决措施部门各项政务性、事务性工作繁杂,深入思考不够,存在“兵来将挡、水来土掩”的惯性思维,今年争取积极发挥综合部参与政务、管理事务、搞好服务的职能作用,力争工作年年有进步,部门职工之间团结协作,把综合部建设成学习型、服务型、素质型、效率型部门。四、下半年工作计划
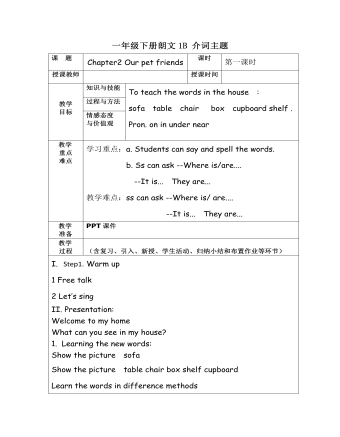
一年级下册朗文1B 介词主题教案
知识与技能To teach the words in the house : sofa table chair box cupboard shelf . Pron. on in under near

北师大初中九年级数学下册正切与坡度1教案
已知一水坝的横断面是梯形ABCD,下底BC长14m,斜坡AB的坡度为3∶3,另一腰CD与下底的夹角为45°,且长为46m,求它的上底的长(精确到0.1m,参考数据:2≈1.414,3≈1.732).解析:过点A作AE⊥BC于E,过点D作DF⊥BC于F,根据已知条件求出AE=DF的值,再根据坡度求出BE,最后根据EF=BC-BE-FC求出AD.解:过点A作AE⊥BC,过点D作DF⊥BC,垂足分别为E、F.∵CD与BC的夹角为45°,∴∠DCF=45°,∴∠CDF=45°.∵CD=46m,∴DF=CF=462=43(m),∴AE=DF=43m.∵斜坡AB的坡度为3∶3,∴tan∠ABE=AEBE=33=3,∴BE=4m.∵BC=14m,∴EF=BC-BE-CF=14-4-43=10-43(m).∵AD=EF,∴AD=10-43≈3.1(m).所以,它的上底的长约为3.1m.方法总结:考查对坡度的理解及梯形的性质的掌握情况.解决问题的关键是添加辅助线构造直角三角形.

北师大初中九年级数学下册垂径定理教案
方法总结:垂径定理虽是圆的知识,但也不是孤立的,它常和三角形等知识综合来解决问题,我们一定要把知识融会贯通,在解决问题时才能得心应手.变式训练:见《学练优》本课时练习“课后巩固提升”第2题【类型三】 动点问题如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.解析:当点P处于弦AB的端点时,OP最长,此时OP为半径的长;当OP⊥AB时,OP最短,利用垂径定理及勾股定理可求得此时OP的长.解:作直径MN⊥弦AB,交AB于点D,由垂径定理,得AD=DB=12AB=4cm.又∵⊙O的直径为10cm,连接OA,∴OA=5cm.在Rt△AOD中,由勾股定理,得OD=OA2-AD2=3cm.∵垂线段最短,半径最长,∴OP的长度范围是3cm≤OP≤5cm.方法总结:解题的关键是明确OP最长、最短时的情况,灵活利用垂径定理求解.容易出错的地方是不能确定最值时的情况.

北师大初中九年级数学下册第一章复习教案
一、本章知识要点: 1、锐角三角函数的概念; 2、解直角三角形。二、本章教材分析: (一).使学生正确理解和掌握三角函数的定义,才能正确理解和掌握直角三角形中边与角的相互关系,进而才能利用直角三角形的边与角的相互关系去解直角三角形,因此三角形函数定义既是本章的重点又是理解本章知识的关键,而且也是本章知识的难点。如何解决这一关键问题,教材采取了以下的教学步骤:1. 从实际中提出问题,如修建扬水站的实例,这一实例可归结为已知RtΔ的一个锐角和斜边求已知角的对边的问题。显然用勾股定理和直角三角形两个锐角互余中的边与边或角与角的关系无法解出了,因此需要进一步来研究直角三角形中边与角的相互关系。2. 教材又采取了从特殊到一般的研究方法利用学生的旧知识,以含30°、45°的直角三角形为例:揭示了直角三角形中一个锐角确定为30°时,那么这角的对边与斜边之比就确定比值为1:2。

北师大初中九年级数学下册切线长定理教案
(3)若要满足结论,则∠BFO=∠GFC,根据切线长定理得∠BFO=∠EFO,从而得到这三个角应是60°,然后结合已知的正方形的边长,也是圆的直径,利用30°的直角三角形的知识进行计算.解:(1)FB=FE,PE=PA;(2)四边形CDPF的周长为FC+CD+DP+PE+EF=FC+CD+DP+PA+BF=BF+FC+CD+DP+PA=BC+CD+DA=23×3=63;(3)假设存在点P,使BF·FG=CF·OF.∴BFOF=CFFG.∵cos∠OFB=BFOF,cos∠GFC=CFFG,∴∠OFB=∠GFC.∵∠OFB=∠OFE,∴∠OFE=∠OFB=∠GFC=60°,∴在Rt△OFB中,BF=OBtan∠OFB=OBtan60°=1.在Rt△GFC中,∵CG=CF·tan∠GFC=CF·tan60°=(23-1)×3=6-3,∴DG=CG-CD=6-33,∴DP=DG·tan∠PGD=DG·tan30°=23-3,∴AP=AD-DP=23-(23-3)=3.方法总结:由于存在性问题的结论有两种可能,所以具有开放的特征,在假设存在性以后进行的推理或计算.一般思路是:假设存在——推理论证——得出结论.若能导出合理的结果,就做出“存在”的判断,若导出矛盾,就做出“不存在”的判断.

北师大初中九年级数学下册圆教案
解析:首先求得圆的半径长,然后求得P、Q、R到Q′的距离,即可作出判断.解:⊙O′的半径是r= 12+12=2,PO′=2>2,则点P在⊙O′的外部;QO′=1<2,则点Q在⊙O′的内部;RO′=(2-1)2+(2-1)2=2=圆的半径,故点R在圆上.方法总结:注意运用平面内两点之间的距离公式,设平面内任意两点的坐标分别为A(x1,y1),B(x2,y2),则AB=(x1-x2)2+(y1-y2)2.【类型四】 点与圆的位置关系的实际应用如图,城市A的正北方向50千米的B处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为100千米,AC是一条直达C城的公路,从A城发往C城的客车车速为60千米/时.(1)当客车从A城出发开往C城时,某人立即打开无线电收音机,客车行驶了0.5小时的时候,接收信号最强.此时,客车到发射塔的距离是多少千米(离发射塔越近,信号越强)?(2)客车从A城到C城共行驶2小时,请你判断到C城后还能接收到信号吗?请说明理由.

北师大初中九年级数学下册圆的对称性教案
我们知道圆是一个旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心.将图中的扇形AOB(阴影部分)绕点O逆时针旋转某个角度,画出旋转之后的图形,比较前后两个图形,你能发现什么?二、合作探究探究点:圆心角、弧、弦之间的关系【类型一】 利用圆心角、弧、弦之间的关系证明线段相等如图,M为⊙O上一点,MA︵=MB︵,MD⊥OA于D,ME⊥OB于E,求证:MD=ME.解析:连接MO,根据等弧对等圆心角,则∠MOD=∠MOE,再由角平分线的性质,得出MD=ME.证明:连接MO,∵ MA︵=MB︵,∴∠MOD=∠MOE,又∵MD⊥OA于D,ME⊥OB于E,∴MD=ME.方法总结:圆心角、弧、弦之间相等关系的定理可以用来证明线段相等.本题考查了等弧对等圆心角,以及角平分线的性质.

北师大初中九年级数学下册正切与坡度2教案
教学目标:1、理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。2、了解计算一个锐角的正切值的方法。教学重点:理解并掌握正切的含义,会在直角三角形中求出某个锐角的正切值。教学难点:计算一个锐角的正切值的方法。教学过程:一、观察回答:如图某体育馆,为了方便不同需求的观众设计了多种形式的台阶。下列图中的两个台阶哪个更陡?你是怎么判断的?图(1) 图(2)[点拨]可将这两个台阶抽象地看成两个三角形答:图 的台阶更陡,理由 二、探索活动1、思考与探索一:除了用台阶的倾斜角度大小外,还可以如何描述台阶的倾斜程度呢?① 可通过测量BC与AC的长度,② 再算出它们的比,来说明台阶的倾斜程度。(思考:BC与AC长度的比与台阶的倾斜程度有何关系?)答:_________________.③ 讨论:你还可以用其它什么方法?能说出你的理由吗?答:________________________.2、思考与探索二:

北师大初中九年级数学下册正弦与余弦1教案
解析:根据锐角三角函数的概念,知sin70°<1,cos70°<1,tan70°>1.又cos70°=sin20°,锐角的正弦值随着角的增大而增大,∴sin70°>sin20°=cos70°.故选D.方法总结:当角度在0°cosA>0.当角度在45°<∠A<90°间变化时,tanA>1.变式训练:见《学练优》本课时练习“课堂达标训练”第10题【类型四】 与三角函数有关的探究性问题在Rt△ABC中,∠C=90°,D为BC边(除端点外)上的一点,设∠ADC=α,∠B=β.(1)猜想sinα与sinβ的大小关系;(2)试证明你的结论.解析:(1)因为在△ABD中,∠ADC为△ABD的外角,可知∠ADC>∠B,可猜想sinα>sinβ;(2)利用三角函数的定义可求出sinα,sinβ的关系式即可得出结论.解:(1)猜想:sinα>sinβ;(2)∵∠C=90°,∴sinα=ACAD ,sinβ=ACAB .∵AD<AB,∴ACAD>ACAB,即sinα>sinβ.方法总结:利用三角函数的定义把两角的正弦值表示成线段的比,然后进行比较是解题的关键.

北师大初中九年级数学下册正弦与余弦2教案
[教学目标]1、 理解并掌握正弦、余弦的含义,会在直角三角形中求出某个锐角的正弦和余弦值。2、能用函数的观点理解正弦、余弦和正切。[教学重点与难点] 在直角三角形中求出某个锐角的正弦和余弦值。[教学过程] 一、情景创设1、问题1:如图,小明沿着某斜坡向上行走了13m后,他的相对位置升高了5m,如果他沿着该斜坡行走了20m,那么他的相对位置升高了多少?行走了a m呢?2、问题2:在上述问题中,他在水平方向又分别前进了多远?二、探索活动1、思考:从上面的两个问题可以看出:当直角三角形的一个锐角的大小已确定时,它的对边与斜边的比值________;它的邻边与斜边的比值________。(根据是__________________。)2、正弦的定义 如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的对边a与斜边c的比叫做∠A的______,记作________,即:sinA=________=________.3、余弦的定义 如图,在Rt△ABC中,∠C=90°,我们把锐角∠A的邻边b与斜边c的比叫做∠A的______,记作=_________,即:cosA=______=_____。(你能写出∠B的正弦、余弦的表达式吗?)试试看.___________.




