-
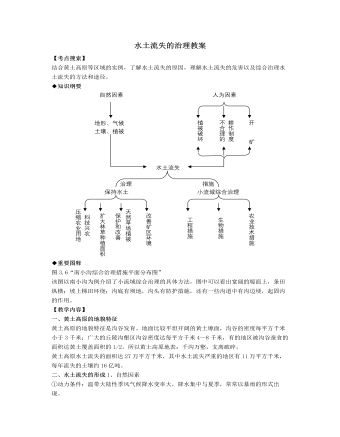
人教版高中地理选修2水土流失的治理教案
2、关于黄土高原小流域及其治理的叙述,正确的是()A.小流域不能看作是一个完整的地域单元B.小流域可以相当于黄土高原上一条河流的整个流域C.小流域综合治理的方针是“保塬、护坡、固沟“D.小流域的综合治理只能采用农业技术措施3、黄土高原植被遭到破坏的原因有()①营造宫殿,毁林开荒②修筑梯田,开石动土③开荒弃荒,轮荒作业④开露天矿,建隔离护坝⑤保塬护坡,打坝建库⑥开挖原生地面,复垦采空矿区A.①②④B.①③⑤C.①③D.②④4、下列关于黄土高原的叙述,正确的是()A.水土流失不可治理B.人为因素是黄土高原现代水土流失的主导因素C.植树种草是做好水土保持的基本前提D.开矿会加剧水土流失,故应少开矿5、引起黄土高原水土流失最直接的因素是()A.降水集中于夏季且多暴雨B.黄土垂直节理发育C.地表崎岖不平,千沟万壑D.不合理开发造成地表黄土裸露,失去植被保护6、治理黄土高原水土流失的工程措施有()A.植树造林B.平整土地C.修建水库D.深耕改土

人教版高中政治选修3美国的联邦制教案
3、联邦制的弊端:(1)、效率不高:(2)、集团分享权力,维护资产阶级的利益,不顾人民要求。在美国实行联邦制的二百多年问,联邦制的弊端也显露无遗。美国联邦制的最大问题是效率不高,联邦政府与州政府之间相互扯皮、推诿,各州政府之间各自为政。全国性资产阶级利益集团与地方性资产阶级利益集团分享权力,对于广大人民群众的要求,资产阶级则利用国家结构形式的特点相互推卸责任。当大多数资产阶级利益集团意见接近时,联邦制既能保护州的灵活性,又能保证中央的权威;当资产阶级利益集团之间矛盾重重时,联邦制就处于低效运转之中。相关链接:1954年,美国最高法院在一项判决中宣布,公立学校实行种族隔离、拒绝黑人入学是违反宪法的。这一裁决引起南方一些州的抵制,一些州竟以暴力阻止黑人进入公立学校。

人教版高中政治选修3国家的本质教案
①含义:即国家管理形式,是国家政权的组织形式②政体的必要性和重要性A、行使职能B、维护其根本利益掌握国家政权的阶级为实现政治统治、行使社会管理职能,必然要采取某种形式组织政权机关。统治阶级为维护其根本利益,总是力求采用最有效的政权组织形式。3、国体与政体的关系(板书)(1)、政体的多样性(2)、国体与政体的关系①国体决定政体,并通过一定的政体来体现;政体体现国体,并服务于特定的国体。适当的政体能够巩固国体,不适当的政体会危害国体。补充:政体由国体决定并反映国体,国体是主要的方面。但是,政体也具有一定的独立性,影响它形成的因素主要有:历史条件、阶级力量对比、传统习惯、国际环境影响等。②专政政体国体与政体,即是国家制度中内容与形式两个方面(3)从国体、政体两个方面看民主制国家补充:专政即是主要依靠暴力实行的统治,它与民主相对立,属于国体的范畴,而专制则与法制相对立,属于政体的范畴。

人教版高中政治选修3美国的利益集团教案
(3)、各种利益集团内部很少有什么民主机制,大都为少数人所控制——从利益集团内部的管理机制看;广大群众常常对某些组织寄予期望,投人力量,但是他们的利益却往往得不到关注。(4)、利益集团为政府腐败提供了肥沃的土壤。利益集团的活动方式,在很大程度上是用金钱购买政治影响力,是一种滋养腐败的行为——从利益集团对政府的负面影响看。实际上,在国会议员、政府官员与利益集团之间,已经形成一种相互依赖的共生关系。3、利益集团机制的隐蔽性、欺骗性及其实质:美国政坛中的利益集团机制,是资产阶级控制国家机器的一种特殊形式,具有相当强的隐蔽性和欺骗性。表面上看,利益集团是所谓的“民意代表”,向政府反映各阶层、群体的观点和利益,实质上是资产阶级在“民意”的幌子下控制权力。

人教版高中政治选修3美国的三权分立教案
国会一直在政治生活中居于主导地位;到了当代,则是总统居于主导地位。由于司法机关无权直接支配社会力量和财富,相比之下,联邦法院力量向来较弱。第二次世界大战后,由于美国一直追逐全球霸权,美国总统的战争权力更加强化,向海外派遣军队的次数更加频繁。美国人民日益觉察到这种不断增长的“帝王般总统职位”可能带来的危险。2、三权分立制的本质——是一种资产阶级民主制度美国的三权分立制本质上是一种资产阶级民主制度。二百多年的历史经验表明,它有效地维护了美国资产阶级的统治。但是,广大劳动人民不可能在这种制度下享有真正的民主。虽然三大权力机关之间互相制约、平衡,却没有一个代表人民意志的权力机关,因而不可能实现人民群众的多数人统治。◇本框题小结:◇3个3种权力:3种权力即立法权、行政权和司法权;3个弊端:即三权分立原则的3 个弊端;3个中央政权机构即立法机关、行政机关和司法机关;◇2个原因:即确立三权分立原则的原因◇1个本质:即三权分立原则的本质

人教版高中地理选修2我国的三大自然区教案
1、中国三大自然区的空间位置和基本特征。2、中国自然区域差异对人类活动的影响。◆重要图释图1.1“三大自然区图”三大自然区的界线(自然地理分界):西北干旱半干旱区与东部季风区之间大致以400mm等年降水量线为界,青藏高寒区与东部季风区约以3000米等高线为界,青藏高寒区与西北干旱半干旱区以昆仑山——阿尔金山——祁连山为界。【学习策略】1、读图分析:通过读图、分析、归纳的方法,识记三大自然区的空间位置、相互界线,理解各自然地理要素的特征和空间分布规律。2、综合训练:运用空白地图,将地理事物落实在图上,并进行比较分析、归纳整理,理解三大自然区的区域差异。【教学内容】一、三大自然区的划分1.三大自然区的划分依据(地貌、气候的地域差异)

北师大初中八年级数学下册三角形的全等和等腰三角形的性质教案
证明:过点A作AF∥DE,交BC于点F.∵AE=AD,∴∠E=∠ADE.∵AF∥DE,∴∠E=∠BAF,∠FAC=∠ADE.∴∠BAF=∠FAC.又∵AB=AC,∴AF⊥BC.∵AF∥DE,∴DE⊥BC.方法总结:利用等腰三角形“三线合一”得出结论时,先必须已知一个条件,这个条件可以是等腰三角形底边上的高,可以是底边上的中线,也可以是顶角的平分线.解题时,一般要用到其中的两条线互相重合.三、板书设计1.全等三角形的判定和性质2.等腰三角形的性质:等边对等角3.三线合一:在等腰三角形的底边上的高、中线、顶角的平分线中,只要知道其中一个条件,就能得出另外的两个结论.本节课由于采用了动手操作以及讨论交流等教学方法,有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中九年级数学下册直线和圆的位置关系及切线的性质教案
解析:(1)由切线的性质得AB⊥BF,因为CD⊥AB,所以CD∥BF,由平行线的性质得∠ADC=∠F,由圆周角定理的推论得∠ABC=∠ADC,于是证得∠ABC=∠F;(2)连接BD.由直径所对的圆周角是直角得∠ADB=90°,因为∠ABF=90°,然后运用解直角三角形解答.(1)证明:∵BF为⊙O的切线,∴AB⊥BF.∵CD⊥AB,∴∠ABF=∠AHD=90°,∴CD∥BF.∴∠ADC=∠F.又∵∠ABC=∠ADC,∴∠ABC=∠F;(2)解:连接BD,∵AB为⊙O的直径,∴∠ADB=90°,∴∠A+∠ABD=90°.由(1)可知∠ABF=90°,∴∠ABD+∠DBF=90°,∴∠A=∠DBF.又∵∠A=∠C,∴∠C=∠DBF.在Rt△DBF中,sin∠DBF=sinC=35,DF=6,∴BF=10,∴BD=8.在Rt△ABD中,sinA=sinC=35,BD=8,∴AB=403.∴⊙O的半径为203.方法总结:运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

小学数学人教版五年级上册《等式的性质》说课稿
说教材>是人教版小学数学五年级上册第五单元P64的内容。在学习本节课之前学生已经认识了等式与方程,这便为本节课的学习(构建等量关系的数学模型)打下一定的基础,同时也为以后解简单方程埋下伏笔,因此本节课内容也是本章中的一个重点。基于本节内容的特点,我将本节课的教学目标确定为:1.知识与技能:理解等式的性质并用语言表述,能利用等式的性质解决简单问题;2.过程与方法:在实验操作、讨论、归纳等活动中,经历探究等式基本性质的过程;3.情感态度与价值观:使学生积极参与数学活动,体验探索等式基本性质的挑战性与得出数学结论的确定性。教学重难点:了解等式的基本性质,并能简单运用。说学情:小学五年级的学生已具备一定的思考能力,又乐于动手操作、合作探究。因此教学中我引导学生认真观察-独立思考-自主探究-合作交流,遵循由浅入深,由具体到抽象的规律,为学生创设一个和谐的学习环境,让孩子们在探索中交流、感受、理解和概括出等式的基本性质。

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中数学八年级上册单个一次函数图象的应用1教案
方法总结:要认真观察图象,结合题意,弄清各点所表示的意义.探究点二:一次函数与一元一次方程一次函数y=kx+b(k,b为常数,且k≠0)的图象如图所示,根据图象信息可求得关于x的方程kx+b=0的解为()A.x=-1B.x=2C.x=0D.x=3解析:首先由函数经过点(0,1)可得b=1,再将点(2,3)代入y=kx+1,可求出k的值为1,从而可得出一次函数的表达式为y=x+1,再求出方程x+1=0的解为x=-1,故选A.方法总结:此题主要考查了一次函数与一元一次方程的关系,关键是正确利用待定系数法求出一次函数的关系式.三、板书设计一次函数的应用单个一次函数图象的应用一次函数与一元一次方程的关系探究的过程由浅入深,并利用了丰富的实际情景,增加了学生的学习兴趣.教学中要注意层层递进,逐步让学生掌握求一次函数与一元一次方程的关系.教学中还应注意尊重学生的个体差异,使每个学生都学有所获.

北师大初中数学八年级上册两个一次函数图象的应用1教案
解:∵y=23x+a与y=-12x+b的图象都过点A(-4,0),∴32×(-4)+a=0,-12×(-4)+b=0.∴a=6,b=-2.∴两个一次函数分别是y=32x+6和y=-12x-2.y=32x+6与y轴交于点B,则y=32×0+6=6,∴B(0,6);y=-12x-2与y轴交于点C,则y=-2,∴C(0,-2).如图所示,S△ABC=12BC·AO=12×4×(6+2)=16.方法总结:解此类题要先求得顶点的坐标,即两个一次函数的交点和它们分别与x轴、y轴交点的坐标.三、板书设计两个一次函数的应用实际生活中的问题几何问题进一步训练学生的识图能力,能通过函数图象获取信息,解决简单的实际问题,在函数图象信息获取过程中,进一步培养学生的数形结合意识,发展形象思维.在解决实际问题的过程中,进一步发展学生的分析问题、解决问题的能力和数学应用意识.

北师大初中数学八年级上册确定一次函数的表达式1教案
解:设正比例函数的表达式为y1=k1x,一次函数的表达式为y2=k2x+b.∵点A(4,3)是它们的交点,∴代入上述表达式中,得3=4k1,3=4k2+b.∴k1=34,即正比例函数的表达式为y=34x.∵OA=32+42=5,且OA=2OB,∴OB=52.∵点B在y轴的负半轴上,∴B点的坐标为(0,-52).又∵点B在一次函数y2=k2x+b的图象上,∴-52=b,代入3=4k2+b中,得k2=118.∴一次函数的表达式为y2=118x-52.方法总结:根据图象确定一次函数的表达式的方法:从图象上选取两个已知点的坐标,然后运用待定系数法将两点的横、纵坐标代入所设表达式中求出待定系数,从而求出函数的表达式.【类型三】 根据实际问题确定一次函数的表达式某商店售货时,在进价的基础上加一定利润,其数量x与售价y的关系如下表所示,请你根据表中所提供的信息,列出售价y(元)与数量x(千克)的函数关系式,并求出当数量是2.5千克时的售价.

北师大初中数学八年级上册数据的离散程度1教案
(4)从平均分看,两队的平均分相同,实力大体相当;从折线的走势看,甲队比赛成绩呈上升趋势,而乙队比赛成绩呈下降趋势;从获胜场数看,甲队胜三场,乙队胜两场,甲队成绩较好;从方差看,甲队比赛成绩比乙队比赛成绩波动小,甲队成绩较稳定.综上所述,选派甲队参赛更能取得好成绩.方法总结:本题是反映数据集中程度与离散程度的综合题.从图形中得到两队的成绩,然后从平均数、方差的角度来考虑,在平均数相同的情况下,方差越小的越稳定.三、板书设计数据的离散程度极差:一组数据中最大数据与最小数据的差方差:各个数据与平均数差的平方的平均数 s2=1n[(x1-x)2+(x2-x)2+…+(xn-x)2]标准差:方差的算术平方根 公式:s=s2经历表示数据离散程度的几个量的探索过程,通过实例体会用样本估计总体的统计思想,培养学生的数学应用能力.通过小组合作,培养学生的合作意识;通过解决实际问题,让学生体会数学与生活的密切联系.

北师大初中数学九年级上册反比例函数的应用1教案
因为反比例函数的图象经过点A(1.5,400),所以有k=600.所以反比例函数的关系式为p=600S(S>0);(2)当S=0.2时,p=6000.2=3000,即压强是3000Pa;(3)由题意知600S≤6000,所以S≥0.1,即木板面积至少要有0.1m2.方法总结:本题渗透了物理学中压强、压力与受力面积之间的关系p= ,当压力F一定时,p与S成反比例.另外,利用反比例函数的知识解决实际问题时,要善于发现实际问题中变量之间的关系,从而进一步建立反比例函数模型.三、板书设计反比例函数的应用实际问题与反比例函数反比例函数与其他学科知识的综合经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程,提高运用代数方法解决问题的能力,体会数学与现实生活的紧密联系,增强应用意识.通过反比例函数在其他学科中的运用,体验学科整合思想.

北师大初中数学九年级上册反比例函数的图象1教案
解:(1)∵点(1,5)在反比例函数y=kx的图象上,∴5=k1,即k=5,∴反比例函数的解析式为y=5x.又∵点(1,5)在一次函数y=3x+m的图象上,∴5=3+m,即m=2,∴一次函数的解析式为y=3x+2;(2)由题意,联立y=5x,y=3x+2.解得x1=1,y1=5或x2=-53,y2=-3.∴这两个函数图象的另一个交点的坐标为(-53,-3).三、板书设计反比例函数的图象形状:双曲线位置当k>0时,两支曲线分别位于 第一、三象限内当k<0时,两支曲线分别位于 第二、四象限内画法:列表、描点、连线(描点法)通过学生自己动手列表、描点、连线,提高学生的作图能力.理解函数的三种表示方法及相互转换,对函数进行认识上的整合,逐步明确研究函数的一般要求.反比例函数的图象具体展现了反比例函数的整体直观形象,为学生探索反比例函数的性质提供了思维活动的空间.

中班数学教案:线的世界
活动重点:找出各种线的特点 活动难点:根据线的某个特征进行分类。 活动准备:1、幼儿收集各种线,丰富相关知识。(如毛线、中国结线、棉线、钓鱼线、电线、尼龙线)2、幼儿操作材料:分类卡、笔、各种各样的线。3、电视机、视频 活动过程:一、导入活动,展示事先收集的各式各样的线。1、师:找出你认识的线,和同伴交流,说说它是什么线?有什么用?什么样子的?

中班数学教案:会变的图形
教学准备: 正方形纸、小刀。 教学过程: (一)变魔术 让幼儿猜想正方形能不能变成三角形、小正方形、长方形。然后将纸折叠,剪开变为各种图形。 将剪开的图形再拼成正方形。

人音版小学音乐二年级下册我是人民小骑兵说课稿
教师与学生有导有游,避免了以往欣赏课教学中枯燥的让学生完整听,分段听,机械式的讨论欣赏,增加了情趣,用不同的音乐活动表现不同的段落,让学生清晰各个段落的旋律与表现内容。2、本课成功之处:创设良好的学习情境,营造良好的学习氛围。学生在学习过程中,通过舞蹈、器乐伴奏等表演感受到了音乐段落的变化,学生清楚的分清段落层次。3、本课失败之处:舞蹈动作的创编如果能更加生动,体现出小骑兵的神气活现会更好。4、生成问题:学生在合作表演时,打击乐器的节奏容易不稳,教师提醒学生注意的同时可以带领学生一起敲击控制好节拍。最后为了丰富学生对音乐的体验,我在这一部分让学生通过欣赏歌曲《草原英雄小姐妹》,感受蒙古音乐的节奏特点,体验并升华情感。5、今后调整思路:舞蹈动作可以创编更生动更有表现力的动作,丰富学生的感受和表现力。

北师大初中数学八年级上册平行线的判定1教案
(2)DF∥BE.∵DE平分∠ADC,BF平分∠ABC(已知),∴∠3=12∠ADC,∠2=12∠ABC(角平分线定义).∵∠ADC=∠ABC(已知),∴∠2=∠3(等量代换).又∵∠1=∠2(已知),∴∠1=∠3(等量代换),∴DF∥BE(内错角相等,两直线平行).(3)AD∥BC.由(2)知∠3=∠1,又∵DE平分∠ADC(已知),∴∠ADE=∠3(角平分线定义),∠ADE=∠1(等量代换).∴∠A=180°-∠ADE-∠1=180°-2∠ADE=180°-∠ADC=180°-∠ABC(三角形内角和为180°及等量代换),即∠A+∠ABC=180°,∴AD∥BC(同旁内角互补,两直线平行).方法总结:解此类题应首先结合图形猜测结论,然后证明.证明两条直线平行,一般先找它们的截线,再求同位角相等(或内错角相等,同旁内角互补)来说明两直线平行.若没有公共截线,则需作出两直线的截线辅助证明.三、板书设计平行线,的判定)判定公理:同位角相等,两直线平行判定定理内错角相等,两直线平行同旁内角互补,两直线平行本节课通过经历探索平行线的判定方法的过程,发展学生的逻辑推理能力,逐步掌握规范的推理论证格式.

