-

特种设备事故应急预案
(一), 起重伤害事故 1,指从事起重作业时引起的机械伤害事故。起重作业包括:桥式起重机、龙门起重机、门座起重机、搭式起重机、悬臂起重机、桅杆起重机、铁路起重机、汽车吊、电动葫芦、千斤顶等作业。如:起重作业时,脱钩砸人,钢丝绳断裂抽人,移动吊物撞人,钢丝绳刮人,滑车碰人等伤害。包括起重机械在使用和安装过程中的倾翻事故及提升设备过卷等事故。

农民工突发事件应急预案
1、全面负责农民工工资突发事件的应急处置工作。2、密切关注项目部是否有拖欠克扣劳动者工资情况,是否有上访事件动态,做到及时发现、及时上报,迅速到位,及时地处理,防止事态进一步扩大。四、处置应急事件程序1、信息报告:发生农民工工资突发事件后,在最短的时间内报告集团相关部门。2、启动预案:突发事件发生后,应急处理小组要在20分钟内做出案情初步判断,并启动应急预案。

人事用工劳动合同
一、工资结算 经过双方互相协商,甲方每月支付给乙方的工资款项为 元,(现金和转账两种方式)。三、甲方须知甲方录用乙方工作之后将按照相关规定安排乙方进行相关工作,不得故意拖欠乙方劳动工资。甲方如在合约期间解除此合同,可提前30天通知乙方。按照国家法定假期为乙方安排假期时间。

单位安全事心得体会8篇
做好安全生产工作犹如履薄冰,来不得半点疏忽和麻痹。作为安全管理者或单位安全第一职责人首先要消除在思想认识上存在的.误区。一是对安全设施的认识误区。随着科学技术的迅猛发展,施工现场安全设施和劳动保护用品也呈现高、精、尖技术,并被广泛运用到生产实践中。由此个别从事安全管理人员或干部就出现盲目乐观思想,认为只要投入这些“精良装备”今后不会再发生安全大问题了,工作中也不注重抓小防大了,这种麻痹思想很可能会导致事故的发生;二是对职工培训的认识误区。主要是我公司是安全生产先进单位,已连续实现安全生产六千多天,大多职工也从事施工生产多年或干过很多个工程,觉得没有再加大培训力度的必要了;再之是专、兼职安全管理人员少,甲方、业主一味追求工期进度,没有时间、力量和精力来深入搞培训;另外新进职工绝大多数是大中专、技校毕业生,已在公司理解过培训部门的安全培训,于是就降低了三级教育网络的培训标准。由于领导重视程度和培训力度不够以及流于形式的状况,而事故恰恰最容易发生在对业务知识生疏、现场安全施工经验少的职工身上。所以,抓紧对职工劳动安全生产的教育,也是有效防止安全事故发生的保障;三是个别安全管理人员或干部思想上的认识误区。执行制度必严、违反制度必究,对待安全生产工作我们都明白“严是爱、松是害”,然而在实际工作中,个别安全管理人员或干部干部对安全管理存在着“三怕”思想:对上怕担职责,对下怕得罪人,对工作怕吃苦受累,造成形式主义、好人主义、官僚主义的严重局面,导致在执行和落实当中出现“缺位”现象。管理能出效益,安全亦出效益,安全生产是涉及职工生命安全的大事,也关系到企业的生存发展和稳定。安全生产需要多管齐下警钟长鸣。

合同盖章:注意事项
以下过程都要必须都要完成,否则合同无效,由于盖章问题导致结算拖延、无法结算问题由乙方自己承担,合同未归档统一不做结算。两方合同一式3份,三方合同一式4份,先由我方公司寄出3(4)份,乙方盖完公章将3(4)份寄回,我方公司盖完章,会将合同寄回乙方。1、提供营业执照复印件并加盖公章(一份),开户许可证复印件并加盖公章(一份)。合同签署人(经纪人)身份证复印件(一份)盖章并按手印。2、合同内容盖章。(1)签署页,手写签署姓名和日期!!

民事诉讼委托代理合同
1、甲方因与 纠纷一案,为了维护自身的合法权益,需要专业的律师代理诉讼;2、乙方是依据《中华人民共和国律师法》并经吉林省司法厅批准设立的律师事务所,具备向社会提供法律服务的资格和能力;3、甲方拟聘请乙方律师代理其参加诉讼活动,乙方予以同意;现双方根据《中华人民共和国合同法》、《中华人民共和国律师法》及相关法律规定,本着自愿、平等、互惠互利、诚实信用的原则,经充分友好协商,订立如下合同条款,以资共同恪守履行:第一条 代理事项1.1乙方接受甲方的委托,采用 方式代理本案,并指派 律师为甲方与 纠纷案的第 审代理人。 1.2乙方指派的上述律师因合理原因(包括但不限于正常调动、离职、时间冲突、回避、身体状况等)无法继续或暂时不能提供服务时,在征得甲方同意后,乙方可以另行指派其他律师继续承办甲方委托的事项,并不得因此而损害甲方的利益。1.3、甲方在乙方指派的律师之外委托第三人代理或者处理本案的,应当经乙方同意。第二条 代理工作范围2.1、乙方的代理工作包括下列事项:整理诉讼证据、撰写诉讼文书,根据诉讼需要到工商、房屋、土地等部门查询、调查档案、参加法庭审理;2.2、根据案件需要及案情进展和所出现的不同情况,乙方应为甲方提出诉讼保全、申请鉴定、申请法院调查取证等方案及撰写相关法律文书。2.3、根据案件需要甲方办理的调查取证、诉讼保全、文书递交及送达、选择鉴定机构、配合法院调查取证、代缴诉讼及其他费用等不属于乙方工作范围,但上述工作需要出具文书的应由乙方撰写并交与甲方。第三条 双方权利义务

大班科学教案:小飞艇变小汽艇
2、通过小飞艇变小汽艇的环节,培养幼儿的观察力、想象力和动手操作能力。 3、让幼儿在玩中不断探索,体验科技活动的乐趣。 活动准备:1、幼儿操作的小飞艇若干过。 2、大水盆6个、餐巾若干。 3、火箭升天的图片、人游泳的图片。 活动重点:感知空气对流成风产生动力,可以推动一些物体运动。 活动难点:通过小飞艇变小汽艇,培养幼儿的观察力、想象力。 活动过程:一、小飞艇 1、出示小飞艇让幼儿观察。 2、提问: 它的名字叫小飞艇,谁能知道它是怎么飞的? (让幼儿充分的说) 3、动手操作 (做成功的幼儿来给其他小朋友分享自己是怎么做的然后再继续操作)

小班数学教案:苹果全家福(大小)
2、知道家有几口,感受家的快乐。 活动准备: 大苹果胸饰一个(正面红色,背面绿色);小苹果胸饰一个;人手一份苹果脸谱;苹果树(挂着与幼儿人数相同的大小,红、绿苹果。);苹果全家福一张;眼镜、头发、小圆片等若干。鼓、录音机、像机。 活动过程: 一、创设情景,激起兴趣 1、观看教师大苹果胸饰,区分颜色。分别观看两教师胸饰,学习区分大小。 2、摘苹果活动:比一比、讲一讲,初步分清大小、颜色。

小班数学教案:按大小对应排序
2、 在活动过程中根据物体的大小特征匹配相应大小的物体。3、 尝试用语言讲述操作过程。活动过程:1、 集体活动。 (1) 给四只大小不同的小猫排序。 教师出示图片小猫,提问:它们是谁?一共有几只?他们有什么不一样?谁会帮它们排队?先带领幼儿数数1、2、3、4只猫,然后大家确定开始的地方,幼儿上来排序,其他幼儿看排大的对不对,并集体讲述她是怎么排序的。(2) 给小猫送鱼。 教师出示三条鱼的图片。问:这是什么?谁最爱吃鱼?那我们把这些鱼送给小猫好吗?看看这些鱼有什么不一样?想想应该怎么送?幼儿操作,师生共同检查,教师引导说出:最小的鱼送给最小的猫,大一点鱼送给大一点的猫,最大的鱼送给最大的猫。大家集体练习一次。

小班数学教案:小动物变魔术
2、乐意参加操作活动,体验成功的快乐。 活动准备: 1、范图;各种小动物的拼图。 3、幼儿用书人手一本。 活动过程: 1、观察完整的小动物拼图。 教师出示完整的小动物拼图。宝宝们,你们看,老师带来了什么?你们认识它们吗? 引导幼儿跟每个小动物问好。

中班数学:《小小飞行员》课件教案
二、重点及难点: 重点:感知8以内的数量 难点:能排除物体大小、颜色的干扰,理解数的实际意义。三、活动准备: 1、纸箱制战斗机(与幼儿人数相等)内有一个,炮弹8发。 2、恶魔城堡情境、小动物若干。四、活动流程: 语言引导、激发兴趣→情景练习、感知数量→排除干扰、巩固练习。五、活动过程:(一)、语言引导、激发兴趣 说明:请幼儿当小小飞行员上蓝天练本领,登上飞机。

实习工作总结
前期跟踪分析预装门开关电机下线率高的问题,并执行临时整改措施,运用质量分析---鱼骨图等工具来分析根本原因和直接原因,然后拿出永久的对策,接着执行及验证对策,最终防止再次发生或在其它产品上发生。通过这次改进,让我了解了公司的改进流程。

实习保密协议
一寸免冠彩色照片一张(蓝底);并附律师事务所关于本所及拟指定的指导律师符合本细则规定条件的情况说明,律师事务所与申请实习人员签订的《实习协议》。接受拟兼职从事律师职业的人员申请实习的,除提交上列规定相关材料外,还应当提交申请实习人员所在的高等院校法学院系或者法学研究单位出具的同意其实习的证明材料。以上材料均应提供原件和1份复印件。省辖市律师协会审核同意的,原件退回,复印件加盖与原件相符章后,与其他申请材料一并归入申请人实习档案。

初中数学人教版二元一次方程组教学设计教案
(一)例题引入篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分。某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?方法一:(利用之前的知识,学生自己列出并求解)解:设剩X场,则负(10-X)场。方程:2X+(10-X)=16方法二:(老师带领学生一起列出方程组)解:设胜X场,负Y场。根据:胜的场数+负的场数=总场数 胜场积分+负场积分=总积分得到:X+Y=10 2X+Y=16

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.
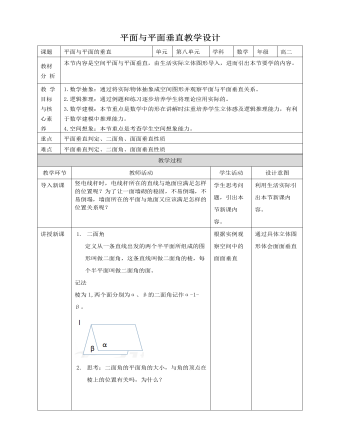
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
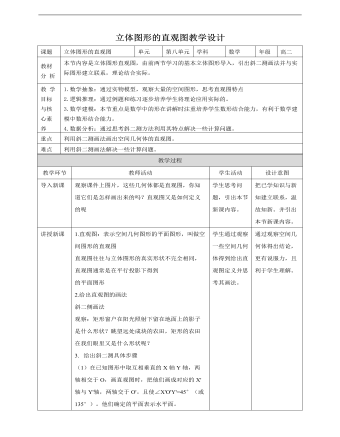
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
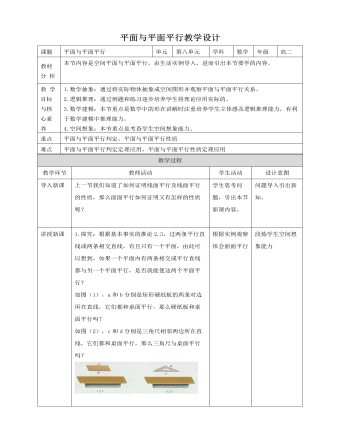
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
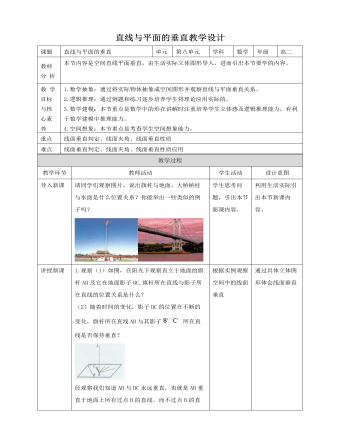
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.

