-
北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时，当天销售利润最大，最大利润是多少？解析：(1)分1≤x＜50和50≤x≤90两种情况进行讨论，利用利润＝每件的利润×销售的件数，即可求得函数的解析式；(2)利用(1)得到的两个解析式，结合二次函数与一次函数的性质分别求得最值，然后两种情况下取最大的即可．解：(1)当1≤x＜50时，y＝(200－2x)(x＋40－30)＝－2x2＋180x＋2000；当50≤x≤90时，y＝(200－2x)(90－30)＝－120x＋12000.综上所述，y＝－2x2＋180x＋2000（1≤x＜50），－120x＋12000（50≤x≤90）；(2)当1≤x＜50时，y＝－2x2＋180x＋2000，二次函数开口向下，对称轴为x＝45，当x＝45时，y最大＝－2×452＋180×45＋2000＝6050；当50≤x≤90时，y＝－120x＋12000，y随x的增大而减小，当x＝50时，y最大＝6000.综上所述，销售该商品第45天时，当天销售利润最大，最大利润是6050元．方法总结：本题考查了二次函数的应用，读懂表格信息、理解利润的计算方法，即利润＝每件的利润×销售的件数，是解决问题的关键．
北师大初中九年级数学下册图形面积的最大值1教案
如图所示，要用长20m的铁栏杆，围成一个一面靠墙的长方形花圃，怎么围才能使围成的花圃的面积最大？如果花圃垂直于墙的一边长为xm，花圃的面积为ym2，那么y＝x(20－2x)．试问：x为何值时，才能使y的值最大？二、合作探究探究点一：二次函数y＝ax2＋bx＋c的最值已知二次函数y＝ax2＋4x＋a－1的最小值为2，则a的值为()A．3 B．－1 C．4 D．4或－1解析：∵二次函数y＝ax2＋4x＋a－1有最小值2，∴a＞0，y最小值＝4ac－b24a＝4a（a－1）－424a＝2，整理，得a2－3a－4＝0，解得a＝－1或4.∵a＞0，∴a＝4.故选C.方法总结：求二次函数的最大(小)值有三种方法，第一种是由图象直接得出，第二种是配方法，第三种是公式法．变式训练：见《学练优》本课时练习“课堂达标训练” 第1题探究点二：利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值
北师大初中九年级数学下册圆内接正多边形教案
解析：正多边形的边心距、半径、边长的一半正好构成直角三角形，根据勾股定理就可以求解．解：(1)设正三角形ABC的中心为O，BC切⊙O于点D，连接OB、OD，则OD⊥BC，BD＝DC＝a.则S圆环＝π·OB2－π·OD2＝πOB2－OD2＝π·BD2＝πa2；(2)只需测出弦BC(或AC，AB)的长；(3)结果一样，即S圆环＝πa2；(4)S圆环＝πa2.方法总结：正多边形的计算，一般是过中心作边的垂线，连接半径，把内切圆半径、外接圆半径、边心距，中心角之间的计算转化为解直角三角形．变式训练：见《学练优》本课时练习“课后巩固提升”第4题【类型四】 圆内接正多边形的实际运用如图①，有一个宝塔，它的地基边缘是周长为26m的正五边形ABCDE(如图②)，点O为中心(下列各题结果精确到0.1m)．(1)求地基的中心到边缘的距离；(2)已知塔的墙体宽为1m，现要在塔的底层中心建一圆形底座的塑像，并且留出最窄处为1.6m的观光通道，问塑像底座的半径最大是多少？
北师大初中九年级数学下册圆周角和圆心角的关系教案
解析：点E是BC︵的中点，根据圆周角定理的推论可得∠BAE＝∠CBE，可证得△BDE∽△ABE，然后由相似三角形的对应边成比例得结论．证明：∵点E是BC︵的中点，即BE︵＝CE︵，∴∠BAE＝∠CBE.∵∠E＝∠E(公共角)，∴△BDE∽△ABE，∴BE∶AE＝DE∶BE，∴BE2＝AE·DE.方法总结：圆周角定理的推论是和角有关系的定理，所以在圆中，解决相似三角形的问题常常考虑此定理．三、板书设计圆周角和圆心角的关系1．圆周角的概念2．圆周角定理3．圆周角定理的推论本节课的重点是圆周角与圆心角的关系，难点是应用所学知识灵活解题．在本节课的教学中，学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握，理解起来问题也不大，而对圆周角与圆心角的关系理解起来则相对困难，因此在教学过程中要着重引导学生对这一知识的探索与理解．还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题，在教学过程中要对此予以足够的强调，借助多媒体加以突出.
北师大初中九年级数学下册直线和圆的位置关系及切线的性质教案
解析：(1)由切线的性质得AB⊥BF，因为CD⊥AB，所以CD∥BF，由平行线的性质得∠ADC＝∠F，由圆周角定理的推论得∠ABC＝∠ADC，于是证得∠ABC＝∠F；(2)连接BD.由直径所对的圆周角是直角得∠ADB＝90°，因为∠ABF＝90°，然后运用解直角三角形解答．(1)证明：∵BF为⊙O的切线，∴AB⊥BF.∵CD⊥AB，∴∠ABF＝∠AHD＝90°，∴CD∥BF.∴∠ADC＝∠F.又∵∠ABC＝∠ADC，∴∠ABC＝∠F；(2)解：连接BD，∵AB为⊙O的直径，∴∠ADB＝90°，∴∠A＋∠ABD＝90°.由(1)可知∠ABF＝90°，∴∠ABD＋∠DBF＝90°，∴∠A＝∠DBF.又∵∠A＝∠C，∴∠C＝∠DBF.在Rt△DBF中，sin∠DBF＝sinC＝35，DF＝6，∴BF＝10，∴BD＝8.在Rt△ABD中，sinA＝sinC＝35，BD＝8，∴AB＝403.∴⊙O的半径为203.方法总结：运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
XX年开学第一周国旗下讲话稿例文
尊敬的老师，亲爱的同学们：大家上午好!我是襄阳长春外国语学校(襄阳四中实验中学)八(3)班的王泽宇，今天我国旗下讲话的题目是《谁让我们是学生》。学生!一个多么响亮的名字，却又干着多么累的差事。每天都是学习学习再学习，作业作业照旧作业，真是太苦了!但是，学习又是多么紧张!说小了，它决定着我们一生的运气和前程;放大了，它决定着社会的生长和国度的壮大。梁启超说过“少年强则国强”，而“强”表如今有知识有文化有技能。要想拥有这些，我们必须学习。我们是学生，祖国的来日是否壮大就牢牢地掌握在我们手里!谁让我们是学生，谁让我们是襄阳四中实验中学的学生!祖国的未来、母校的光辉需要我们去创造!所以我们不怕苦，不怕累，靠着勤奋和毅力一直在求学的道路上坚持着。每天早晨，人们还在熟睡，连太阳公公都还在梦乡时，我们已经活跃在塑胶跑道上。响亮的背书声划破天际，整齐的脚步声震动大地，新的一天在我们的欢呼声中开始。
人教版高中数学选修3分类加法计数原理与分步乘法计数原理(1)教学设计
问题1. 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号，总共能编出多少种不同的号码？因为英文字母共有26个，阿拉伯数字共有10个，所以总共可以编出26+10=36种不同的号码.问题2.你能说说这个问题的特征吗？上述计数过程的基本环节是：（1）确定分类标准，根据问题条件分为字母号码和数字号码两类；（2）分别计算各类号码的个数；（3）各类号码的个数相加，得出所有号码的个数.你能举出一些生活中类似的例子吗？一般地，有如下分类加法计数原理：完成一件事，有两类办法. 在第1类办法中有m种不同的方法，在第2类方法中有n种不同的方法，则完成这件事共有:N= m+n种不同的方法.二、典例解析例1.在填写高考志愿时，一名高中毕业生了解到，A,B两所大学各有一些自己感兴趣的强项专业，如表，
人教版高中数学选修3分类加法计数原理与分步乘法计数原理(2)教学设计
当A,C颜色相同时,先染P有4种方法,再染A,C有3种方法,然后染B有2种方法,最后染D也有2种方法.根据分步乘法计数原理知,共有4×3×2×2=48(种)方法;当A,C颜色不相同时,先染P有4种方法,再染A有3种方法,然后染C有2种方法,最后染B,D都有1种方法.根据分步乘法计数原理知,共有4×3×2×1×1=24(种)方法.综上,共有48+24=72(种)方法.故选B.答案:B5.某艺术小组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?解:由题意可知,在艺术小组9人中,有且仅有1人既会钢琴又会小号(把该人记为甲),只会钢琴的有6人,只会小号的有2人.把从中选出会钢琴与会小号各1人的方法分为两类.第1类,甲入选,另1人只需从其他8人中任选1人,故这类选法共8种;第2类,甲不入选,则会钢琴的只能从6个只会钢琴的人中选出,有6种不同的选法,会小号的也只能从只会小号的2人中选出,有2种不同的选法,所以这类选法共有6×2=12(种).因此共有8+12=20(种)不同的选法.
2022年山东省滨州市中考语文真题（原卷版）
阅读下面唐诗，完成下面小题。漫成一首杜甫江月去人只数尺，风灯①照夜欲三更。沙头宿鹭联拳②静，船尾跳鱼拨刺③鸣。【注释】①风灯：船中桅杆上挂着的灯，有纸罩能避风。②联拳：指夜宿的白鹭屈曲着身子，三五成群团聚在沙滩上。拳，屈曲。③拨刺：拟声词，指鱼在水里跳动发出的声音。11. 这首诗通过“_____________”“风灯”“宿鹭”“_________________”等意象，描绘出一幅恬淡平和的江上月夜图。
2022年辽宁省营口市中考语文真题（原卷版）
（二）（4分）阅读下面诗歌，完成下面小题。瀑布联句李忱千岩万壑不辞劳，远看方知出处高。溪涧焉能留得住，终归大海作波涛。14. 首句运用了什么手法？有什么表达效果？15. 请简要分析最后两句寄寓了作者怎样的情怀？
广西贺州市2021年中考语文试题（原卷版）
先帝知臣谨慎，故临崩寄臣以大事也。受命以来，夙夜忧叹，恐托付不效，以伤先帝之明；故五月渡泸，深入不毛。今南方已定，兵甲已足，当奖率三军，北定中原，庶竭驽钝，攘除奸凶，兴复汉室，还于旧都。此臣所以报先帝而忠陛下之职分也。至于斟酌损益，进尽忠言，则攸之、祎、允之任也。
广西百色市2021年中考语文试题（解析版）
历史老师无奈地说过：“有次我让大家整理近代史的笔记，别人都是两三张纸就搞定了，你知道崔安然写了多少吗？56页！唉……”数学老师总结道：“崔安然啊……就是单纯的脑子笨。”我还听隔壁班的王梦茹同学说，她俩是发小，上学时崔安然在学习方面就认真而吃力，效果不理想。
广西百色市2021年中考语文试题（原卷版）
我开始格外关注这个笨小孩：凌乱的头发，额头上此消彼长的痘痘，瘦小的肩膀……明明是单薄的小姑娘，身体里却像是有使不完的能量，面对大大小小的挫折时她波澜不惊、一往无前地继续努力，偶有一丝焦虑掠过，也稍纵即逝。我不知道那压力如山的一天又一天，崔安然究竟是怎么扛下来的……这一切，都令人心疼。
广西玉林市2021年中考语文真题（解析版）
之后，阿根廷决赛战胜联邦德国，获得了1986年世界杯冠军，马拉多纳凭借5个进球、5个助攻获得金球奖。1990年，马拉多纳带领阿根廷队获得世界杯亚军。1994年，马拉多纳带领阿根廷队再度冲击世界杯，结果因药检阳性禁赛，这导致阿根廷队军心大乱，止步八分之一决赛。1997年10月，马拉多纳宣布退役。
广西梧州市2021年中考语文试题（原卷版）
哲人有言，英雄的业绩、他们的言论，就是那个时代的精华。的确，英雄是一个民族的“凝结核”。如杨靖宇所言，“革命就像火一样，任凭大雪封山，鸟兽藏迹，只要我们有火种，就能驱赶严寒，带来光明和温暖。”英雄就是这革命的火种，没有英雄的引领，个体的力量就难以凝聚；缺少先锋的领路，前行的方向将难以看清。马克思因此感慨，“每一个社会时代都需要有自己的伟大人物”。
广西桂林市2021年中考语文试题（解析版）
山不在高，有仙则名。水不在深，有龙则灵。斯是陋室，惟吾德馨。苔痕上阶绿，草色入帘青。谈笑有鸿儒，往来无白丁。可以调素琴，阅金经。无丝竹之乱耳，无案牍之劳形。南阳诸葛庐，西蜀子云亭。孔子云：何陋之有？
2022年湖南省怀化市中考语文真题（解析版）
【海外网2月21日电】2月20日，北京冬奥会正式闭幕，这届冬奥会为世界留下了独具特色的中国记忆，收获了众多好评，各国运动员持续发文为北京冬奥会点赞。“感谢、祝福”成了高频词。
2022年湖北省宜昌市中考语文真题（原卷版）
倘若意犹未尽，试看杨万里的《郡中送春盘》：“饼如茧纸不可风，菜如缥茸劣可缝。韭芽卷黄苣舒紫，芦服削冰寒脱齿。”白如茧纸的是春饼，吃的时候，从春盘里夹取菜蔬各一小箸，卷为细简状，这便是咬春饼。
2022年浙江省绍兴市中考语文真题（解析版）
“无废城市”，是以创新、协调、绿色、开放、共享的新发展理念为引领，通过推动形成绿色发展方式和生活方式，持续推进固体废物源头减量和资源化利用，最大限度减少填埋量，将固体废物环境影响降至最低的城市发展模式。2017年，中国工程院院士杜祥豌在国内首次牵头提出创建“无废城市”及“无废社会”的建议。
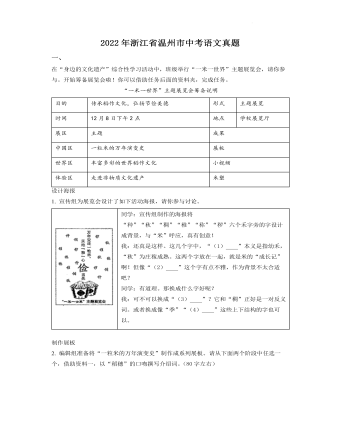
2022年浙江省温州市中考语文真题（解析版）
桃花峪是黄河中下游分界线，把桥建在这里自有讲究。我个人的选择原因，就实用层面来讲，自是离老家更近，却也有非实用层面：是它的外形更时尚更壮观，名字我也格外钟爱：桃花峪——黄河——大桥，既明艳又铿锵，既坚固又绵长，不是么？