-

北师大初中七年级数学下册同底数幂的乘法教案
问题:2015年9月24日,美国国家航空航天局(下简称:NASA)对外宣称将有重大发现宣布,可能发现除地球外适合人类居住的星球,一时间引起了人们的广泛关注.早在2014年,NASA就发现一颗行星,这颗行星是第一颗在太阳系外恒星旁发现的适居带内、半径与地球相若的系外行星,这颗行星环绕红矮星开普勒186,距离地球492光年.1光年是光经过一年所行的距离,光的速度大约是3×105km/s.问:这颗行星距离地球多远(1年=3.1536×107s)?3×105×3.1536×107×492=3×3.1536×4.92×105×107×102=4.6547136×10×105×107×102.问题:“10×105×107×102”等于多少呢?二、合作探究探究点:同底数幂的乘法【类型一】 底数为单项式的同底数幂的乘法计算:(1)23×24×2;(2)-a3·(-a)2·(-a)3;(3)mn+1·mn·m2·m.解析:(1)根据同底数幂的乘法法则进行计算即可;(2)先算乘方,再根据同底数幂的乘法法则进行计算即可;(3)根据同底数幂的乘法法则进行计算即可.

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示

北师大初中九年级数学下册利用三角函数测高2教案
问题2、如何用测角仪测量一个低处物体的俯角呢?和测量仰角的步骤是一样的,只不过测量俯角时,转动度盘,使度盘的直径对准低处的目标,记下此时铅垂线所指的度数,同样根据“同角的余角相等”,铅垂线所指的度数就是低处的俯角.活动三:测量底部可以到达的物体的高度.“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.要测旗杆MN的高度,可按下列步骤进行:(如下图)1.在测点A处安置测倾器(即测角仪),测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).根据测量数据,就能求出物体MN的高度.在Rt△MEC中,∠MCE=α,AN=EC=l,所以tanα= ,即ME=tana·EC=l·tanα.又因为NE=AC=a,所以MN=ME+EN=l·tanα+a.
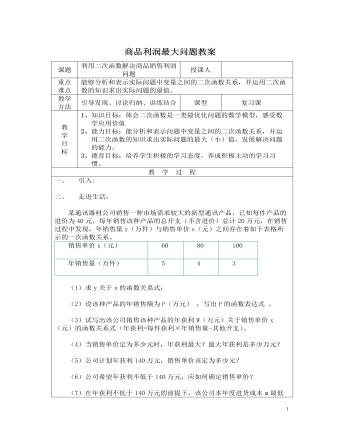
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?
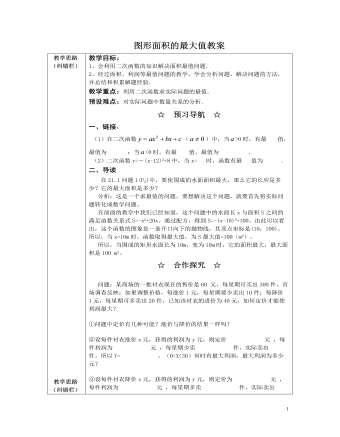
北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中七年级数学下册角平分线的性质教案
解析:根据AB∥CD,∠ACD=120°,得出∠CAB=60°.再根据尺规作图得出AM是∠CAB的平分线,即可得出∠MAB的度数.解:∵AB∥CD,∴∠ACD+∠CAB=180°.又∵∠ACD=120°,∴∠CAB=60°.由尺规作图知AM是∠CAB的平分线,∴∠MAB=12∠CAB=30°.方法总结:通过本题要掌握角平分线的作图步骤,根据作图明确AM是∠BAC的角平分线是解题的关键.三、板书设计1.角平分线的性质:角平分线上的点到这个角的两边的距离相等.2.角平分线的作法本节课由于采用了动手操作以及讨论交流等教学方法,从而有效地增强了学生对角以及角平分线的性质的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生在性质的运用上还存在问题,需要在今后的教学与作业中进一步的加强巩固和训练

北师大初中七年级数学下册单项式除以单项式教案
光的速度约为3×108米/秒,一颗人造地球卫星的速度是8×103米/秒,则光的速度是这颗人造地球卫星速度的多少倍?解析:要求光速是人造地球卫星的速度的倍数,用光速除以人造地球卫星的速度,可转化为单项式相除问题.解:(3×108)÷(8×103)=(3÷8)·(108÷103)=3.75×104.答:光速是这颗人造地球卫星速度的3.75×104倍.方法总结:解整式除法的实际应用题时,应分清何为除式,何为被除式,然后应当单项式除以单项式法则计算.三、板书设计1.单项式除以单项式的运算法则:单项式相除,把系数、同底数幂分别相除,作为商的因式;对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.2.单项式除以单项式的应用在教学过程中,通过生活中的情景导入,引导学生根据单项式乘以单项式的乘法运算推导出其逆运算的规律,在探究的过程中经历数学概念的生成过程,从而加深印象

北师大初中七年级数学下册单项式与单项式相乘教案
解析:先求出长方形的面积,再求出绿化的面积,两者相减即可求出剩下的面积.解:长方形的面积是xym2,绿化的面积是35x×34y=920xy(m2),则剩下的面积是xy-920xy=1120xy(m2).方法总结:掌握长方形的面积公式和单项式乘单项式法则是解题的关键.三、板书设计1.单项式乘以单项式的运算法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里面含有的字母,则连同它的指数作为积的一个因式.2.单项式乘以单项式的应用本课时的重点是让学生理解单项式的乘法法则并能熟练应用.要求学生在乘法的运算律以及幂的运算律的基础上进行探究.教师在课堂上应该处于引导位置,鼓励学生“试一试”,学生通过动手操作,能够更为直接的理解和应用该知识点

北师大初中七年级数学下册利用“边边边”判定三角形全等教案
解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n边形的一个顶点可以作(n-3)条对角线,把多边形分成(n-2)个三角形,所以,要使一个n边形木架不变形,至少需要(n-3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.三、板书设计1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”.2.三角形的稳定性本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练

北师大初中七年级数学下册线段垂直平分线的性质教案
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可求出△ADE≌△FCE,根据全等三角形的性质即可解答;(2)根据线段垂直平分线的性质判断出AB=BF即可解答.解:(1)∵AD∥BC,∴∠ADC=∠ECF.∵E是CD的中点,∴DE=EC.又∵∠AED=∠CEF,∴△ADE≌△FCE,∴FC=AD;(2)∵△ADE≌△FCE,∴AE=EF,AD=CF.又∵BE⊥AE,∴BE是线段AF的垂直平分线,∴AB=BF=BC+CF.∵AD=CF,∴AB=BC+AD.方法总结:此题主要考查线段的垂直平分线的性质等几何知识.线段垂直平分线上的点到线段两个端点的距离相等,利用它可以证明线段相等.探究点二:线段垂直平分线的作图如图,某地由于居民增多,要在公路l边增加一个公共汽车站,A,B是路边两个新建小区,这个公共汽车站C建在什么位置,能使两个小区到车站的路程一样长(要求:尺规作图,保留作图痕迹,不写画法)?

北师大初中七年级数学下册与面积相关的等可能事件的概率教案
方法总结:当某一事件A发生的可能性大小与相关图形的面积大小有关时,概率的计算方法是事件A所有可能结果所组成的图形的面积与所有可能结果组成的总图形面积之比,即P(A)=事件A所占图形面积总图形面积.概率的求法关键是要找准两点:(1)全部情况的总数;(2)符合条件的情况数目.二者的比值就是其发生的概率.探究点二:与面积有关的概率的应用如图,把一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为________.解析:∵一个圆形转盘按1∶2∶3∶4的比例分成A、B、C、D四个扇形区域,∴圆形转盘被等分成10份,其中B区域占2份,∴P(落在B区域)=210=15.故答案为15.三、板书设计1.与面积有关的等可能事件的概率P(A)= 2.与面积有关的概率的应用本课时所学习的内容多与实际相结合,因此教学过程中要引导学生展开丰富的联想,在日常生活中发现问题,并进行合理的整合归纳,选择适宜的数学方法来解决问题

北师大初中八年级数学下册不等式的基本性质教案
【类型二】 根据不等式的变形确定字母的取值范围如果不等式(a+1)x<a+1可变形为x>1,那么a必须满足________.解析:根据不等式的基本性质可判断a+1为负数,即a+1<0,可得a<-1.方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.三、板书设计1.不等式的基本性质性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变;性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变;性质3:不等式的两边都乘(或除以)同一个负数,不等号方向改变.2.把不等式化成“x>a”或“x<a”的形式“移项”依据:不等式的基本性质1;“将未知数系数化为1”的依据:不等式的基本性质2、3.本节课学习不等式的基本性质,在学习过程中,可与等式的基本性质进行类比,在运用性质进行变形时,要注意不等号的方向是否发生改变;课堂教学时,鼓励学生大胆质疑,通过练习中易出现的错误,引导学生归纳总结,提升学生的自主探究能力.

北师大初中八年级数学下册多边形的内角和与外角和教案
方法总结:解题的关键是由题意列出不等式求出这个少算的内角的取值范围.探究点二:多边形的外角和定理【类型一】 已知各相等外角的度数,求多边形的边数正多边形的一个外角等于36°,则该多边形是正()A.八边形 B.九边形C.十边形 D.十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【类型二】 多边形内角和与外角和的综合运用一个多边形的内角和与外角和的和为540°,则它是()A.五边形 B.四边形C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n=3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.

北师大初中八年级数学下册同分母分式的加减教案
解析:(1)先把第二个分式的分母y-x化为-(x-y),再把分子相加减,分母不变;(2)先把第二个分式的分母a-b化为-(b-a),再把分子相加减,分母不变.解:(1)原式=2x2-3y2x-y-x2-2y2x-y=2x2-3y2-(x2-2y2)x-y=x2-y2x-y=(x+y)(x-y)x-y=x+y;(2)原式=2a+3bb-a-2bb-a-3bb-a=2a+3b-2b-3bb-a=2a-2bb-a=-2(b-a)b-a=-2.方法总结:分式的分母互为相反数时,可以把其中一个分母放到带有负号的括号内,把分母化为完全相同.再根据同分母分式相加减的法则进行运算.三、板书设计1.同分母分式加减法法则:fg±hg=f±hg.2.分式的符号法则:fg=-f-g,-fg=f-g=-fg.本节课通过同分母分数的加减法类比得出同分母分式的加减法.易错点一是符号,二是结果的化简.在教学中,让学生参与课堂探究,进行自主归纳,并对易错点加强练习.从而让学生对知识的理解从感性认识上升到理性认识.

北师大初中八年级数学下册一元一次不等式的应用教案
有三种购买方案:购A型0台,B型10台;A型1台,B型9台;A型2台,B型8台;(2)240x+200(10-x)≥2040,解得x≥1,∴x为1或2.当x=1时,购买资金为12×1+10×9=102(万元);当x=2时,购买资金为12×2+10×8=104(万元).答:为了节约资金,应选购A型1台,B型9台.方法总结:此题将现实生活中的事件与数学思想联系起来,属于最优化问题,在确定最优方案时,应把几种情况进行比较.三、板书设计应用一元一次不等式解决实际问题的步骤:实际问题――→找出不等关系设未知数列不等式―→解不等式―→结合实际问题确定答案本节课通过实例引入,激发学生的学习兴趣,让学生积极参与,讲练结合,引导学生找不等关系列不等式.在教学过程中,可通过类比列一元一次方程解决实际问题的方法来学习,让学生认识到列方程与列不等式的区别与联系.

北师大初中八年级数学下册线段的垂直平分线教案
∵∠DAE=∠DAF,∠AED=∠AFD,AD=AD,∴△ADE≌△ADF,∴AE=AF,DE=DF,∴直线AD垂直平分线段EF.方法总结:当一条直线上有两点都在同一线段的垂直平分线上时,这条直线就是该线段的垂直平分线,解题时常需利用此性质进行线段相等关系的转化.三、板书设计1.线段的垂直平分线的性质定理线段垂直平分线上的点到这条线段两个端点的距离相等.2.线段的垂直平分线的判定定理到一条线段两个端点距离相等的点,在这条线段的垂直平分线上.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因此本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对线段垂直平分线性质定理的逆定理理解不透彻,还需在今后的教学和作业中进一步进行巩固和提高.

北师大初中八年级数学下册旋转的定义和性质教案
(3)∵AD=4,DE=1,∴AE=42+12=17.∵对应点到旋转中心的距离相等且F是E的对应点,∴AF=AE=17.(4)∵∠EAF=90°(旋转角相等)且AF=AE,∴△EAF是等腰直角三角形.【类型二】 旋转的性质的运用如图,点E是正方形ABCD内一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3则∠BE′C=________度.解析:连接EE′,由旋转性质知BE=BE′,∠EBE′=90°,∴△BEE′为等腰直角三角形且∠EE′B=45°,EE′=22.在△EE′C中,EE′=22,E′C=1,EC=3,由勾股定理逆定理可知∠EE′C=90°,∴∠BE′C=∠BE′E+∠EE′C=135°.三、板书设计1.旋转的概念将一个图形绕一个顶点按照某个方向转动一个角度,这样的图形运动称为旋转.2.旋转的性质一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角,对应线段相等,对应角相等.
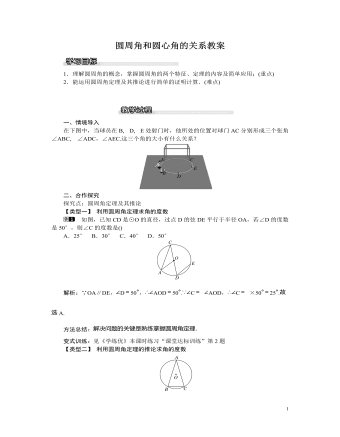
北师大初中九年级数学下册圆周角和圆心角的关系教案
解析:点E是BC︵的中点,根据圆周角定理的推论可得∠BAE=∠CBE,可证得△BDE∽△ABE,然后由相似三角形的对应边成比例得结论.证明:∵点E是BC︵的中点,即BE︵=CE︵,∴∠BAE=∠CBE.∵∠E=∠E(公共角),∴△BDE∽△ABE,∴BE∶AE=DE∶BE,∴BE2=AE·DE.方法总结:圆周角定理的推论是和角有关系的定理,所以在圆中,解决相似三角形的问题常常考虑此定理.三、板书设计圆周角和圆心角的关系1.圆周角的概念2.圆周角定理3.圆周角定理的推论本节课的重点是圆周角与圆心角的关系,难点是应用所学知识灵活解题.在本节课的教学中,学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握,理解起来问题也不大,而对圆周角与圆心角的关系理解起来则相对困难,因此在教学过程中要着重引导学生对这一知识的探索与理解.还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题,在教学过程中要对此予以足够的强调,借助多媒体加以突出.





















