-

北师大初中七年级数学下册三角形的三边关系教案
方法总结:绝对值的化简首先要判断绝对值符号里面的式子的正负,然后根据绝对值的性质将绝对值的符号去掉,最后进行化简.此类问题就是根据三角形的三边关系,判断绝对值符号里面式子的正负,然后进行化简.三、板书设计1.三角形按边分类:有两边相等的三角形叫做等腰三角形,三边都相等的三角形是等边三角形,三边互不相等的三角形是不等边三角形.2.三角形中三边之间的关系:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既增加了学习兴趣,又增强了学生的动手能力

北师大初中七年级数学下册用尺规作三角形教案
【类型三】 已知三边作三角形已知三条线段a、b、c,用尺规作出△ABC,使BC=a,AC=b、AB=c.解:作法:1.作线段BC=a;2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.三、板书设计1.已知两边及其夹角作三角形2.已知两角及其夹边作三角形3.已知三边作三角形本节课学习了有关三角形的作图,主要包括两种基本作图:作一条线段等于已知线段,作一个角等于已知角.作图时,鼓励学生一边作图,一边用几何语言叙述作法,培养学生的动手能力、语言表达能力

北师大初中七年级数学下册与摸球相关的等可能事件的概率教案
1.进一步理解概率的意义并掌握计算事件发生概率的方法;(重点)2.了解事件发生的等可能性及游戏规则的公平性.(难点)一、情境导入一个箱子中放有红、黄、黑三个小球,三个人先后去摸球,一人摸一次,一次摸出一个小球,摸出后放回,摸出黑色小球为赢,那么这个游戏是否公平?二、合作探究探究点一:与摸球有关的等可能事件的概率【类型一】 摸球问题一个不透明的盒子中放有4个白色乒乓球和2个黄色乒乓球,所有乒乓球除颜色外完全相同,从中随机摸出1个乒乓球,摸出黄色乒乓球的概率为()A.23 B.12 C.13 D.16解析:根据题意可得不透明的袋子里装有6个乒乓球,其中2个黄色的,任意摸出1个,则P(摸到黄色乒乓球)=26=13.故选C.方法总结:概率的求法关键是找准两点:①全部情况的总数;②符合条件的情况数目.二者的比值就是其发生的概率.【类型二】 与代数知识相关的问题已知m为-9,-6,-5,-3,-2,2,3,5,6,9中随机取的一个数,则m4>100的概率为()A.15 B.310 C.12 D.35

北师大初中八年级数学下册不等式的基本性质教案
【类型二】 根据不等式的变形确定字母的取值范围如果不等式(a+1)x<a+1可变形为x>1,那么a必须满足________.解析:根据不等式的基本性质可判断a+1为负数,即a+1<0,可得a<-1.方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.三、板书设计1.不等式的基本性质性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变;性质2:不等式的两边都乘(或除以)同一个正数,不等号的方向不变;性质3:不等式的两边都乘(或除以)同一个负数,不等号方向改变.2.把不等式化成“x>a”或“x<a”的形式“移项”依据:不等式的基本性质1;“将未知数系数化为1”的依据:不等式的基本性质2、3.本节课学习不等式的基本性质,在学习过程中,可与等式的基本性质进行类比,在运用性质进行变形时,要注意不等号的方向是否发生改变;课堂教学时,鼓励学生大胆质疑,通过练习中易出现的错误,引导学生归纳总结,提升学生的自主探究能力.

北师大初中八年级数学下册多边形的内角和与外角和教案
方法总结:解题的关键是由题意列出不等式求出这个少算的内角的取值范围.探究点二:多边形的外角和定理【类型一】 已知各相等外角的度数,求多边形的边数正多边形的一个外角等于36°,则该多边形是正()A.八边形 B.九边形C.十边形 D.十一边形解析:正多边形的边数为360°÷36°=10,则这个多边形是正十边形.故选C.方法总结:如果已知正多边形的一个外角,求边数可直接利用外角和除以这个角即可.【类型二】 多边形内角和与外角和的综合运用一个多边形的内角和与外角和的和为540°,则它是()A.五边形 B.四边形C.三角形 D.不能确定解析:设这个多边形的边数为n,则依题意可得(n-2)×180°+360°=540°,解得n=3,∴这个多边形是三角形.故选C.方法总结:熟练掌握多边形的内角和定理及外角和定理,解题的关键是由已知等量关系列出方程从而解决问题.

北师大初中八年级数学下册分式方程的概念及列分式方程教案
探究点二:列分式方程某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x个,根据题意可列分式方程为()A.20x+10x+4=15 B.20x-10x+4=15C.20x+10x-4=15 D.20x-10x-4=15解析:设原计划每天生产x个,则实际每天生产(x+4)个,根据题意可得等量关系:(原计划20天生产的零件个数+10个)÷实际每天生产的零件个数=15天,根据等量关系列出方程即可.设原计划每天生产x个,则实际每天生产(x+4)个,根据题意得20x+10x+4=15.故选A.方法总结:此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,找出题目中的等量关系,列出方程.三、板书设计1.分式方程的概念2.列分式方程本课时的教学以学生自主探究为主,通过参与学习的过程,让学生感受知识的形成与应用的价值,增强学习的自觉性,体验类比学习思想的重要性,然后结合生活实际,发现数学知识在生活中的广泛应用,感受数学之美.

北师大初中九年级数学下册三角函数的应用2教案
教学目标(一)教学知识点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的应用.2.能够把实际问题转化为数学问题,能够借助于计算器进行有关三角函数的计算,并能对结果的意义进行说明.(二)能力训练要求发展学生的数学应用意识和解决问题的能力.(三)情感与价值观要求1.在经历弄清实际问题题意的过程中,画出示意图,培养独立思考问题的习惯和克服困难的勇气. 2.选择生活中学生感兴趣的题材,使学生能积极参与数学活动,提高学习数学、学好数学的欲望.教具重点1.经历探索船是否有触礁危险的过程,进一步体会三角函数在解决问题过程中的作用.2.发展学生数学应用意识和解决问题的能力.教学难点根据题意,了解有关术语,准确地画出示意图.教学方法探索——发现法教具准备多媒体演示
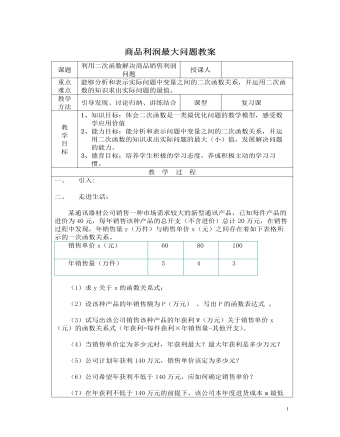
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册切线的判定及三角形的内切圆教案
解析:(1)连接BI,根据I是△ABC的内心,得出∠1=∠2,∠3=∠4,再根据∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,得出∠BIE=∠IBE,即可证出IE=BE;(2)由三角形的内心,得到角平分线,根据等腰三角形的性质得到边相等,由等量代换得到四条边都相等,推出四边形是菱形.解:(1)BE=IE.理由如下:如图①,连接BI,∵I是△ABC的内心,∴∠1=∠2,∠3=∠4.∵∠BIE=∠1+∠3,∠IBE=∠5+∠4,而∠5=∠1=∠2,∴∠BIE=∠IBE,∴BE=IE;(2)四边形BECI是菱形.证明如下:∵∠BED=∠CED=60°,∴∠ABC=∠ACB=60°,∴BE=CE.∵I是△ABC的内心,∴∠4=12∠ABC=30°,∠ICD=12∠ACB=30°,∴∠4=∠ICD,∴BI=IC.由(1)证得IE=BE,∴BE=CE=BI=IC,∴四边形BECI是菱形.方法总结:解决本题要掌握三角形的内心的性质,以及圆周角定理.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册确定二次函数的表达式1教案
解析:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,根据对称轴是x=-3,求出b=6,即可得出答案;(2)根据CD∥x轴,得出点C与点D关于x=-3对称,根据点C在对称轴左侧,且CD=8,求出点C的横坐标和纵坐标,再根据点B的坐标为(0,5),求出△BCD中CD边上的高,即可求出△BCD的面积.解:(1)把点A(-4,-3)代入y=x2+bx+c得16-4b+c=-3,∴c-4b=-19.∵对称轴是x=-3,∴-b2=-3,∴b=6,∴c=5,∴抛物线的解析式是y=x2+6x+5;(2)∵CD∥x轴,∴点C与点D关于x=-3对称.∵点C在对称轴左侧,且CD=8,∴点C的横坐标为-7,∴点C的纵坐标为(-7)2+6×(-7)+5=12.∵点B的坐标为(0,5),∴△BCD中CD边上的高为12-5=7,∴△BCD的面积=12×8×7=28.方法总结:此题考查了待定系数法求二次函数的解析式以及二次函数的图象和性质,注意掌握数形结合思想与方程思想的应用.

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

北师大初中九年级数学下册图形面积的最大值2教案
③设每件衬衣降价x元,获得的利润为y元,则定价为 元 ,每件利润为 元 ,每星期多卖 件,实际卖出 件。所以Y= 。(0<X<20)何时有最大利润,最大利润为多少元?比较以上两种可能,衬衣定价多少元时,才能使利润最大?☆ 归纳反思 ☆总结得出求最值问题的一般步骤:(1)列出二次函数的解析式,并根据自变量的实际意义,确定自变量的取值范围;(2)在自变量的取值范围内,运用公式法或通过配方法求出二次函数的最值。☆ 达标检测 ☆ 1、用长为6m的铁丝做成一个边长为xm的矩形,设矩形面积是ym2,,则y与x之间函数关系式为 ,当边长为 时矩形面积最大.2、蓝天汽车出租公司有200辆出租车,市场调查表明:当每辆车的日租金为300元时可全部租出;当每辆车的日租金提高10元时,每天租出的汽车会相应地减少4辆.问每辆出租车的日租金提高多少元,才会使公司一天有最多的收入?

北师大初中九年级数学下册三角函数的应用1教案
然后,她沿着坡度是i=1∶1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度(参考数据:2≈1.41,结果精确到0.1米).解析:作辅助线EF⊥AC于点F,根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,通过平角减去其他角从而得到∠AEF=45°,即可求出AE的长度.解:作EF⊥AC于点F,根据题意,得CE=18×15=270(米). ∵tan∠CED=1,∴∠CED=∠DCE=45°.∵∠ECF=90°-45°-15°=30°,∴EF=12CE=135米.∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°-45°-60°-30°=45°,∴AE=2EF=1352≈190.4(米).所以,娱乐场地所在山坡AE的长度约为190.4米.方法总结:解决本题的关键是能借助仰角、俯角和坡度构造直角三角形,并结合图形利用三角函数解直角三角形.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

北师大初中九年级数学下册圆周角和圆心角的关系教案
解析:点E是BC︵的中点,根据圆周角定理的推论可得∠BAE=∠CBE,可证得△BDE∽△ABE,然后由相似三角形的对应边成比例得结论.证明:∵点E是BC︵的中点,即BE︵=CE︵,∴∠BAE=∠CBE.∵∠E=∠E(公共角),∴△BDE∽△ABE,∴BE∶AE=DE∶BE,∴BE2=AE·DE.方法总结:圆周角定理的推论是和角有关系的定理,所以在圆中,解决相似三角形的问题常常考虑此定理.三、板书设计圆周角和圆心角的关系1.圆周角的概念2.圆周角定理3.圆周角定理的推论本节课的重点是圆周角与圆心角的关系,难点是应用所学知识灵活解题.在本节课的教学中,学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握,理解起来问题也不大,而对圆周角与圆心角的关系理解起来则相对困难,因此在教学过程中要着重引导学生对这一知识的探索与理解.还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题,在教学过程中要对此予以足够的强调,借助多媒体加以突出.

人教部编版语文八年级下册写作学写读后感教案
师小结:本篇习作开篇概述原作内容,抓住要点,简明扼要。感想的内容,先扣住深沉的父爱,表达自己对傅雷的敬意,然后赞美现实生活中父爱的伟大。思路清晰,情感真挚。【设计意图】以《傅雷家书》读后感写作为例,指导学生如何写读后感。重点指导“点引议联结”的基本结构,让学生写作有章可循。四、尝试写读后感1.写作内容师:同学们已经阅读了《傅雷家书》,请大家回顾内容,自拟题目,按照今天讲的写读后感的方法,先列出写作提纲,再写成作文,不少于600字。2.能力提升用已学的读后感知识,修改自己的作文。并反思所写读后感是否有以下不足:(1)以“引”代“感”。读后感,顾名思义,主要是写“感”,引述是为写“感”服务的,但有些同学往往忘记了这一条,本末倒置,大量抄录或复述原文,结果犯了以“引”代“感”、代“联”的毛病。

人教部编版语文八年级下册综合性学习古诗苑漫步教案
解说词:画卷上的竹子,在石缝中挺然而立,坚韧不拔,遇风不倒。郑板桥先生借竹抒发了自己的洒脱与豁达,表现了他勇敢面对现实、绝不屈服于挫折的品性,令竹子人格化了。此时,“诗是无形画,画是有形诗”。4.声情并茂诵古诗(播放相关的主题图片和音乐,尽量让诗歌和音乐、画面相融合)主持人:诗除了追求意境的图画美之外,还特别注重节奏和韵律,具有音乐美。我们理解了诗中的情愫后,便可以通过朗读来诠释这种种情愫,或低声絮语,或慷慨悲吟,或温情述说……请大家选择自己最喜欢的一首诗词或一小节诗歌,用你认为最贴切的情感和方式朗读,并说出这样处理的原因,或讲述你与此诗有关的故事。朗读示例:无言/独上西楼,月/如钩,寂寞梧桐/深院/锁/清秋。剪不断,理还乱,是离愁,别是/一般滋味/在心头。解说词:此词是南唐后主李煜被囚于宋时所作,表达了他离乡去国的锥心之痛。朗读时要表现出那种深切的故国之思、亡国之恨。

人教版高中地理选修1第二章第三节月相和潮汐教案
创设情境、激发兴趣(5分钟)教师:(锁住屏幕)月相变化与我们人类关系十 分密切。美国著名总统林肯在年轻时担任律师期间曾利用月相变化规律,为当事人进行了成功的辩护,赢得了人们的尊重。月相变化是怎样变化的?月相变化有什么规律,这就是我们今天学习内容。(边演示 学习软件边介绍)我们今天学习主要有三个任务,其中学习任务一要注意在空格中填写农历日期,不认识有关月相的请参照下面的相关学习软件。 完成学习任务二时要注意运用学习软件,首先点击月相,观察日地与月地连线的关系,再观察月亮出没时间现太阳的关系。如满月时,日地与月地连线成1800夹角,当太阳从东方升起时,月亮从西方落下(6时);当太阳从西方落下时,月亮从东方升起 (18时)。满月可见时间是18时到第二天6时。学习任务三请你先判 断图中月相是否正确,如果不正确,请把你认为正确的月相拖到图中适当位置。下面请你们开始学习。

部编版语文七年级下册《记闻一多先生》教案
3、文章怎样写“作为争取民主的战士”的闻一多先生的“说”与“做”的? 文章先写他的“说”,写他“说”的事实,由“小声说”到“向全国人民呼喊”,写他“说”的内容与目的反对独裁,争取民主。再叙他的“做”:起稿政治传单,在群众大会上大骂特务,走在游行示威队伍的前头,昂首挺胸,长须飘飘。用他的“说”和“做”揭示其争取民主、反对独裁的大无畏精神。 4、细读全文,画出精辟的语句,然后复述课文大意,并说出闻一多前期和后期思想品格上的主要特点,前后期有什么变化,又有什么共同的地方。闻先生前期为了探索其救国救民的出路而潜心学术,不畏艰辛,废寝忘食,十数年如一日,终于在学术上取得累累硕果。后期则投身于民主运动,敢于为人民讲话,面对凶残的敌人无所畏惧,视死如归,体现出民主战士的大勇,成为中国革命知识分子的楷模。闻先生在前期和后期所走的道路不同,反映了他对社会认识的变化。但作为一名卓越的学者,一名伟大的爱国者,一名言行一致的志士仁人,他却是始终如一的。



