-
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
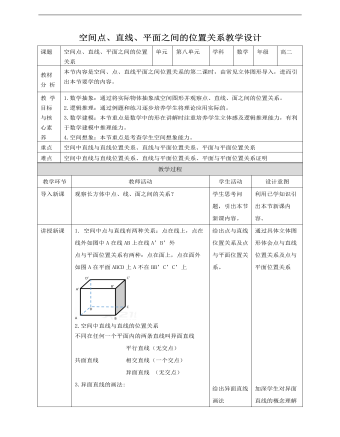
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.

人教A版高中数学必修一正切函数的图像与性质教学设计(2)
本节课是三角函数的继续,三角函数包含正弦函数、余弦函数、正切函数.而本课内容是正切函数的性质与图像.首先根据单位圆中正切函数的定义探究其图像,然后通过图像研究正切函数的性质. 课程目标1、掌握利用单位圆中正切函数定义得到图象的方法;2、能够利用正切函数图象准确归纳其性质并能简单地应用.数学学科素养1.数学抽象:借助单位圆理解正切函数的图像; 2.逻辑推理: 求正切函数的单调区间;3.数学运算:利用性质求周期、比较大小及判断奇偶性.4.直观想象:正切函数的图像; 5.数学建模:让学生借助数形结合的思想,通过图像探究正切函数的性质. 重点:能够利用正切函数图象准确归纳其性质并能简单地应用; 难点:掌握利用单位圆中正切函数定义得到其图象.

人教A版高中数学必修一正弦函数、余弦函数的图像教学设计(2)
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系. 数学学科素养1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修二立体图形直观图教学设计
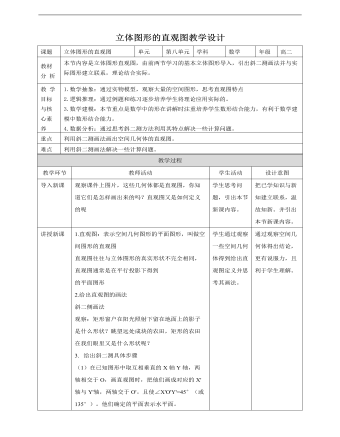
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
人教A版高中数学必修二平面与平面平行教学设计
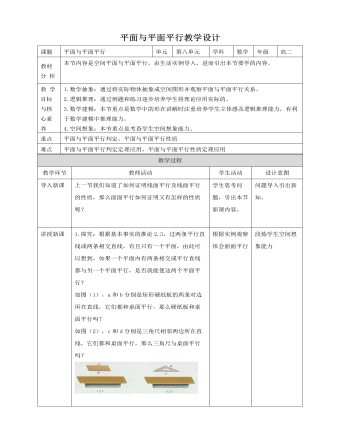
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
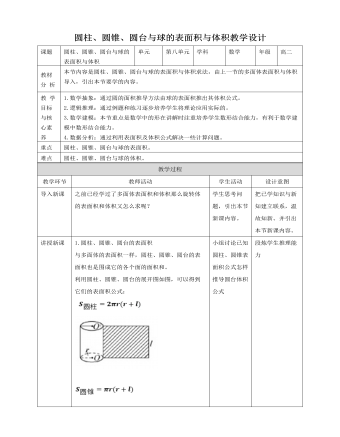
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二向量的减法运算教学设计
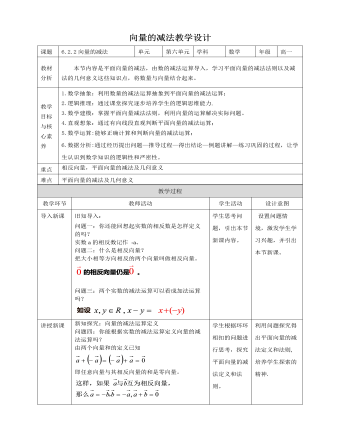
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
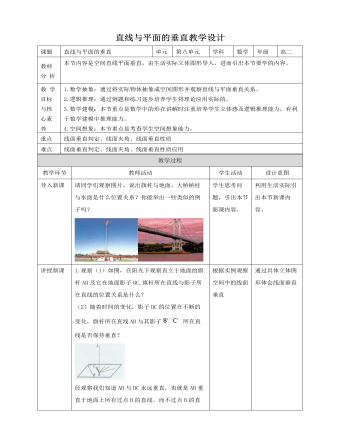
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
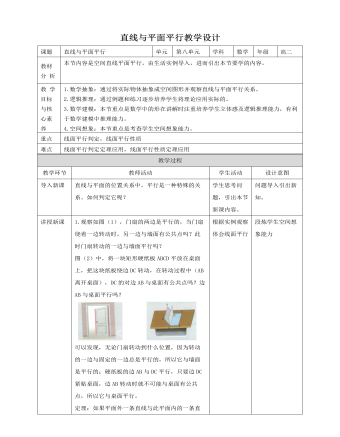
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

高中历史人教版必修一《马克思主义的诞生》说课稿
一、教学理念在新课改精神指导下,我在本课教学中力求贯彻以下教学理念:新课标的指引观 、生本位的学生观、探究式的学习观、多角色的教师观、 发展性的评价观二、教材地位《马克思主义的诞生》是人教版必修一第五单元第18课内容,本课讲述的是国际共产主义运动范畴的历史,是人类社会进入一个新的发展时期。从总体上概述了社会主义从空想到科学,从理论到实践的历程。说明了科学社会主义理论是历史发展的必然结果。本课在国际工运史上占有重要的地位。通过学习学生可对马克思主义加深了解,理解人类历史发展的必然趋势以及人类一直不断追求进步的精神,帮助学生树立正确的人生观、价值观,达到以史鉴今,服务现实的目的。

人教版高中语文必修1《包身工》说课稿2篇
(一)解题:包身工──旧社会一种变相的贩卖奴隶的形式。被贩卖的多是女孩子由承办人送到工厂做工,无人身自由,所得工资全部归承办人所有,在这种形式下做工的人也称包身工。包身工是指二三十年代(时间),在上海东洋纱厂里(地点),为外国人工作的女工(工作性质)。因为这些女工在进厂时已经签订了卖身契,失去了人身的自由权,所以被称为“包身工”。标题中的“包身”二字,突出了帝国主义、封建势力对中国女童工的残酷剥削的罪行,控诉了他们的野蛮残暴的统治手段,以激起人们的义愤和同情,这是全文的中心思想。(二)关于报告文学:《包身工》属于报告文学。(同类题材有初中的《地质之光》、《谁是最可爱的人》)报告文学,是文学体裁的一种,散文的一类,是文艺通讯、速写、特写的总称,是文学创作中的“轻骑兵”。

人教版高中语文必修1《优美的汉字》说课稿
明确:(1)结绳记事说。原始记事的一种方法。人类在没有发明文字或文字使用尚不普遍时,常用在绳索或类似物件上打结的方法记录数字,表达某种意思,用以传达信息,处理事件。 (2)书画说。(3)仓颉造字说。中国自古就有仓颉造字之说。文字的发明是人类发展史上一件石破天惊的大事,它将人们的思维、语言、经验以及复杂的社会现象记录下来,使文化得以传播交流、世代传承。2、汉字的形体:中华民族五千年的历史中,汉字的演变,从甲骨文--金文--大篆--小篆--隶书--草书--楷书--行书,字形由象形到点横竖撇捺的方块字,经历了漫长的岁月。其中凝聚着民族的智慧,也体现出汉字逐步完善的过程,凸显其方方正正、四平八稳的特点。汉字又是一种文化的体现,那些经过艺术处理的汉字或跳起了拉丁舞、有的如同酒醉的成龙打起了醉拳,更是让我们感到的是在欣赏汉字在纸张上跳舞,所以:书法是“纸上的舞蹈”。请大家看到书上的相关内容,注意每一种形体的汉字的载体是什么,其功能又有什么不一样。

人教版高中语文必修1《烛之武退秦师》说课稿2篇
4、本文的重点是说辞,虽仅百余字,却委婉曲折,步步进逼,层层深入,表现出高超的劝说艺术、游说技巧。让学生细细品味并概括说辞中包含几层意思。第一层(“秦、晋围郑,郑既知亡矣”),分析形势,以退为进,博得好感。第二层(“若亡郑而有益于君”至“君之薄也”),亡郑陪邻,动摇联盟。第三层(“若舍郑以为东道主”至“君亦无所害”),存郑有益,利益引诱。第四层(“且君尝为晋君赐矣”至“唯君图之”),追溯历史,深入离间。可见烛之武面对大国的君主,巧舌如簧,不卑不亢,从容辞令,既不刺激对方也不失本国尊严,语言的分寸掌握得恰到好处。表现出烛之武机智善辩的外交才能。5、面对风云突变的局势,晋侯没有感情用事,而表现了清醒的头脑和理智的判断。这种隐忍不发、随机应变的胸怀和谋略,正是晋文公终成霸业的根本原因。设计意图:本环节的重点是全面把握烛之武这一人物性格特征,以及退秦师过程中体现出的非凡的胆识以及高超的谋略和语言艺术。

人教版高中语文必修2《短歌行》说课稿2篇
一、说教材《短歌行》是普通高中课程标准实验教科书必修(二)第二单元的一篇略读课文,本单元安排的是先秦到南北朝时期的诗歌。《短歌行》是著名政治家、军事家、文学家曹操的作品。诗中抓住“忧”字来写诗人为什么“忧”,如何解“忧”,从而表达希望能够招揽人才、完成统一天下的雄心壮志。所以本单元安排《短歌行》一诗,对学生全面了解曹操,感受曹操在短暂的人生中竭力创造伟业的气概。二、说学生我这一课的教学对象是高一学生。他们进入高中学习的时间只有三个多月,现在已经完成了必修(一)的学习。学习了现代诗歌单元,有了一定的诗歌学习基础,初步掌握了读诗的基本方法,但是还未能形成成熟的稳定的学习方式。同时,本单元学习是高中第一次接触古代诗歌,诗歌语言上的障碍和时间上的跨度对他们来说都是学习上的困难。因此教师要引导学生自主学习,合作学习,为他们设置新的学习情境,提供合作探究的机会。

人教版高中语文必修3《杜甫诗三首》说课稿
我以以《登高》为例,引导学生进行意象分析,感悟意境美。古人云“立象以尽意”“古诗之妙,专求意象”意象是诗人情感的载体,是诗歌的灵魂。引导学生张开联想和想象的翅膀去感受,去体验是意象,诗歌鉴赏的关键。科林伍德说“真正艺术的作品,不是看见的,也不是听到的,而是想象中的某种东西。”诗人通过想象创造出诗的形象,我们读者通过想象丰富地再现诗人创造的形象。而感受体验则是以全部身心投入作品,心灵与心灵相沟通,感情与感情相交流,对诗人的想象活动进行再经历和再体验。因此,在引导意象解读中,我先让学生点击这一个,就是通过抓修饰词、依据感情基调、展开想象具体分析本诗中每个意象的情感意蕴和审美意蕴,使学生明白意象在每首诗中的独特性。

人教版高中语文必修3《寡人之于国也》说课稿2篇
(明确:“寡人之于国也,尽心焉耳矣”,但“寡人之民不加多,何也?”)②他认为自己对国家政务尽心尽力了,他有哪些具体做法?(明确:移民移粟)③第2—4节中孟子是怎样说明梁惠王移民移粟的措施与“邻国之政”并无本质区别的?(明确:孟子不直接回答“民不加多”的问题,而是用梁惠王熟悉的“战”设喻——设圈套,诱使对方在不知不觉中说出“不可,直不百步耳,是亦走也。”)④孟子认为怎样才能做到“王道之始”?要想“王道之成”还需采取哪些措施?(明确:“不违农时,谷不可胜食也。数罟不入氵夸池,鱼鳖不可胜食也。斧斤以时入山林,材木不可胜用也。谷与鱼鳖不可胜食,材木不可胜用五亩之宅,树之以桑,五十者可以衣帛矣。鸡豚狗彘之畜,无失其时,七十者可以食肉矣。百亩之田,勿夺其时,数口之家,可以无饥矣。谨库序之教,申之以孝涕之义,颁白者不负戴于道路矣。)这一小步的目的是想让学生通过这些问题的解答,可以进一步理清思路,掌握文的大概内容。

人教版高中语文必修3《师说》说课稿3篇
一、设计理念教学设计坚持少讲多学、以学为主的教学理念,重视学培养生的学习兴趣,要充分调动学生学习的积极性和主动性,充分发挥学生的主体性。教师要以组织者、引导者、合作者的角色参与到教学活动中去。力图通过导学案努力培养学生的自学习惯和自学能力。二、教材分析与处理1、教材的地位与作用:必修三第三单元所选的文言文都是古代的议论性散文。本课是“唐宋八大家”之首、中唐古文运动的倡导者韩愈的力作,是唐宋散文中的名篇,具有很强的代表性。通过这篇自读课的学习,能使学生了解唐宋散文的风貌,更能使学生进一步积累文言文基础知识,提高学生的文言文阅读欣赏能力,从而提升学生的文言文自读能力。2、教学目标:《高中语文课程标准》要求高中学生能阅读浅易文言文,能借助注释和工具书,理解词句含义,读懂文章内容;了解并梳理常见的文言实词、文言虚词、文言句式的意义或用法,注重在阅读实践中举一反三;对文章有一定的分析欣赏能力。高一的学生对于文言文的知识还在积累阶段,应该注重基础知识的积累和一定量的诵读。对此,我将教学目标确定为:

