-

新人教版高中英语必修2Unit 1 Cultural Heritage-Reading For Writing教案
This report is short, concise and has typical news content and language features. The title uses the verb phrases, embodying the characteristics of being concise and general. The introduction is the first two sentences in the first paragraph, describing the general situation of the cultural heritage protection project, including time, place, characters, events and other news elements, so that readers can see the main points of the news report at a glance. The main body is the second and third paragraphs, which report the important historical and cultural value of Mogao Grottoes and the production of Mogao Grottoes Material digital photos, which are of great significance to the inheritance of historical culture and the promotion of international cultural understanding, exchange and cooperation. Direct citation is used in the report, as well as background introduction and other news writing techniques.1. Get students to have a good understanding of some features about a news report by reading the text.2. Instruct students to write a summary about a news report properly using some newly acquired writing skills in this period.3. Develop students’ writing and cooperating abilities.4. Strengthen students’ great interest in writing discourses.1. Stimulate students to have a good understanding of how to a summary about a news report 2. Cultivate students to write a news report properly and concisely.Step 1: Lead in Do you think it is necessary for us to circulate our cultural heritage to the world? Why or why not?Do we need to learn more about other countries’ cultural heritage? Why or why not?Step 2: Read to discover details concerning the main body of the news report.

新人教版高中英语必修2Unit 2 Wildlife Protection-Discovering Useful Structure教案一
The activity topic of this section is "report an ongoing event", and the structure is the passive voice of present continuous tense. Rare wild animals are suffering from large-scale poaching, and species are on the brink of danger. Rescue operations are underway. "Being" and "suffering" are the meanings of the present progressive passive voice.The usage of present progressive passive voice is of great importance in writing a good discourse and appreciating some difficult language items, so it is vital to master it and use it flexibly in a context.1. Motivate Ss to deepen the understanding of the usage of present progressive passive voice in a fixed context.2. Enable Ss to master the usage of present progressive passive voice and use it flexibly in a context.3. Lead Ss to construct sentences or appreciate sentences used master it and use it flexibly in a context.1. Help students to appreciate the function of the usage of present progressive passive voice in a sentence2. Instruct students to write essays using the proper usage of present progressive passive voice.Look at the picture and tell me what are workers doing? What is the house being done?

新人教版高中英语必修2Unit 2 Wildlife Protection-Reading and Thinking教案一
The listening and speaking part aims at how to protect and help endangered animals by listening, speaking and talking about the facts and reasons. This lesson analyzes the decreasing clause of Tibetan antelope population and the measures of protecting Tibetan antelopes. So students can be guided to learn to analyse the title and use different reading skills or strategies, like scanning, skimming and careful reading.1. Read quickly to get the main ideas and the purpose of going to Tibetan; read carefully to understand what the author see and think.2. Understand the sentences of the present continuous passive voice such as “Much is being done to protect wildlife.” and the inverted sentence “Only when we learn to exist in harmony with nature can we stop being a threat to wildlife and to our planet.”3. Enhance the awareness of protecting wildlife.4. Cultivate the reading methods according to different materials.1. Read quickly to get the main ideas and the purpose of going to Tibetan; read carefully to understand what the author see and think.2. Understand the sentences of the present continuous passive voice such as “Much is being done to protect wildlife.” and the inverted sentence “Only when we learn to exist in harmony with nature can we stop being a threat to wildlife and to our planet.”3. Cultivate the reading methods according to different materials.Step 1 Leading-inWatch a video about elephants and whales and then ask:Why are they endangered ? They are killed/hunted

新人教版高中英语必修2Unit 2 Wildlife Protection-Reading and Thinking教案二
The theme of this unit is human and nature, focusing on the theme of wildlife protection. Nature is a complex ecosystem, in which there are delicate balance between animals and plants. Because of the role of the food chain, the extinction of one species will produce influence, causing a series of chain reaction. Large scale extinction of species will have a serious and even irreversible impact on the ecosystem, resulting in immeasurable losses. Therefore, it is of great significance to protect wild species. To protect wild species is to protect human beings themselves. The motto of this unit is "when the buying stops, the killing can too,” which is a public service advertising slogan to protect wildlife. It tells people that every rhinoceros horn, every fur, every bowl of shark fin soup, every Ivory product, and every tiger bone product, etc. consumed by human beings, are innocent wild animals slaughtered behind them. The mission of wild aid is to ban illegal trade in endangered wildlife and mitigate climate change. It aims to educate the public to reduce the consumption demand for endangered wildlife products through public publicity and improve the awareness of environmental protection.1. Improve the awareness of wildlife protection by acquiring the knowledge of wildlife protection.2. Focus on environmental protection and protection of all lives.3. Analysis of the living environment of wild animals with appropriate thinking mode.4. Skillfully use the vocabulary and grammar knowledge of this unit to cultivate self-study ability according to the unit content5. Develop cooperative learning ability through discussion and other ways1. Enable the Ss to talk about the current situation of wild animals.2. Guide the Ss to summarize the main idea of each paragraph as well as the main idea of the text.

新人教版高中英语必修2Unit 4 History and Traditions-Discovering Useful Structure教案一
Step 5 Practice一、完成下列句子。1. Judy and I _______________(把车停下来(park))in an underground car Park near Trafalgar Square, where we could ______________________(让我们的车充电(charge)).2. When we finally reached the service desk to ask for audio guides, we heard it ___________ that there were no audio guides____________(留下,剩下).3. We__________________________(发现自己对...很惊讶)the large number of visitors and the amount of noise at the entrance of the National Gallery.4. Judy ____________________(眼神专注于) Van Gogh’s Sunflowers. It was hard to approach the painting as there were so many people around.5. She ____________________(把这幅画的复制品装箱(box)) to ensure that it was delivered safely.答案:1.had our car parked get our car battery charged 2. announced left 3. found ourselves very surprised 4. had her eyes fixed on 5. had a copy of the painting boxed二、用过去分词对下列句子进行改写。1. Loch Ness was surrounded by beautiful natural landscape, which made it look amazing.2. Carl and his friend stayed with a generous family who offered them bread with butter and honey that was homemade.3. The family’s ancestors once attended to soldiers who were wounded in the First World War.4. The young people were attracted by the legend of Loch Ness. They watched over the lake with their cameras and binoculars, which were positioned on the hill.答案:1. Loch Ness surrounded by beautiful natural landscape looks amazing.2. Carl and his friends stayed with a generous family who offered them homemade bread with butter and honey.3. The family’s ancestors once attended to wounded soldiers in the First World War.4. The young people attracted by the legend of Loch Ness watched over the lake with their cameras and binoculars positioned on the hill.

新人教版高中英语必修2Unit 4 History and Traditions-Discovering Useful Structure教案二
This teaching period mainly deals with grammar: The past participle is used as attributive and objective complement.1. Guide students to review the basic usages of the past participle used as attributive and objective complement.2. Lead students to learn to use some special cases concerning the past participle used as attributive and objective complement flexibly.3. Strengthen students’ great interest in grammar learning.1. Help students to appreciate the function of the past participle used as attributive and objective complement.2. Instruct students to write essays using the past participle used as attributive and objective complement.Step1:温故而知新。Analyze the underlined phrases and then sum up the common usages of the past participles.1.(教材P41)They had castles built(build) all around England, and made changes to the legal system.2.(教材P42)They use the same flag, known(know) as the Union Jack,...3.(教材P42)Judy and I had our car parked(park) in an underground car park near Trafalgar Square, where we could get our car battery charged(charge).Common points: f the past participle used as attributive and objective complement.Step 2:过去分词作定语时的意义1.及物动词的过去分词作定语,在语态上表示被动;在时间上,常表示动作已经发生或完成,有时也不表示时间性。Our teacher watched us doing the experiment and gave us a satisfied smile at last.我们的老师看着我们做实验,最后给了我们一个满意的微笑。The plan put forward at the meeting will be carried out soon.会上提出的计划将很快被执行。2.不及物动词的过去分词作定语,它不表示被动意义,只强调动作完成。Many little kids like gathering fallen leaves in the yard.

新人教版高中英语必修2Unit 4 History and Traditions-Reading and Thinking教案二
Step 5 While reading---Task 3Read the text again and answer the following questions.Q1: How many countries does the UK consist of ?4 Q2: What are the four countries of the United Kingdom?England, Wales, Scotland and Northern Ireland Q3: Which two were the first to be joined together ?England and WalesQ4: What are the two chief advantages of studying the history of a country ?The first one is to help you understand more about the country and its traditions.The second one is to make visiting it more enjoyable.Q5: What’s the author’s attitude towards studying the history ?Supportive/positiveStep 6 Post reading---Retell the textThe United Kingdom, Great Britain, Britain, England—many people are confused by (1)_____ these different names mean. In the 16th century, the nearby country of Wales (2) __________(join) to the Kingdom of England. In the 19 th century, the Kingdom of Ireland was added to create the United Kingdom of Great Britain and Ireland. Finally, the southern part of Ireland (3) ______ (break) away from the UK, which resulted in the full name we have today. However, most people just use the (4)_________(shorten) name: the UK. The four countries (5)__________ belong to the United Kingdom work together in some areas. There were four sets of invaders and the last group were the Normans. They had castles (6)_________(build) all around England and made changes (7)__________ the legal system. Studying the history of the country will make your visit much more (8)_________(enjoy). The capital city London is (9)___ ancient port city that has a history (10)______(date) back to Roman times. 1. what 2.was joined 3.broke 4.shortened 5.that 6. built 7.to 8.enjoyable 9.an 10.dating Step 6 Homework

新人教版高中英语必修2Unit 4 History and traditions教案
这个地区有着深厚的传统。既学既练:为了让更多的外国游客了解中国文化,欣赏中国美丽的自然风光,感受中国发生的巨大变化,某外文杂志社将出版一本英语小册子来介绍中国的旅游景点。该杂志社邀请你为该小册子写一篇英语短文来介绍杭州,内容包括:1.杭州的位置(中国东南部)、面积(16 000多平方公里)及历史(2 200多年)等;2.杭州的旅游特色(自然风景、传统文化、特色小吃等);3.希望更多的游客来杭州参观。注意:1.词数80左右;2.可适当增加细节,以使行文连贯。Located in the southeast of China, Hangzhou is a beautiful city.Dating back more than 2,200 years, Hangzhou covers an area of more than 16,000 square kilometers.In Hangzhou, you can visit the West Lake, whose scenery is fascinating.In addition, you can’t miss its cultural relics and historical sites, from which you will learn more about excellent Chinese traditional culture and traditions.In Hangzhou, the special snacks are famous and visitors from different parts of the world think highly of them.As a tourist attraction, Hangzhou attracts a large number of visitors from home and abroad every year.Once you come to China, Hangzhou is a scenic spot you can’t miss.

人教版高中数学选修3分类加法计数原理与分步乘法计数原理(1)教学设计
问题1. 用一个大写的英文字母或一个阿拉伯数字给教室里的一个座位编号,总共能编出多少种不同的号码?因为英文字母共有26个,阿拉伯数字共有10个,所以总共可以编出26+10=36种不同的号码.问题2.你能说说这个问题的特征吗?上述计数过程的基本环节是:(1)确定分类标准,根据问题条件分为字母号码和数字号码两类;(2)分别计算各类号码的个数;(3)各类号码的个数相加,得出所有号码的个数.你能举出一些生活中类似的例子吗?一般地,有如下分类加法计数原理:完成一件事,有两类办法. 在第1类办法中有m种不同的方法,在第2类方法中有n种不同的方法,则完成这件事共有:N= m+n种不同的方法.二、典例解析例1.在填写高考志愿时,一名高中毕业生了解到,A,B两所大学各有一些自己感兴趣的强项专业,如表,

人教版高中数学选修3分类加法计数原理与分步乘法计数原理(2)教学设计
当A,C颜色相同时,先染P有4种方法,再染A,C有3种方法,然后染B有2种方法,最后染D也有2种方法.根据分步乘法计数原理知,共有4×3×2×2=48(种)方法;当A,C颜色不相同时,先染P有4种方法,再染A有3种方法,然后染C有2种方法,最后染B,D都有1种方法.根据分步乘法计数原理知,共有4×3×2×1×1=24(种)方法.综上,共有48+24=72(种)方法.故选B.答案:B5.某艺术小组有9人,每人至少会钢琴和小号中的一种乐器,其中7人会钢琴,3人会小号,从中选出会钢琴与会小号的各1人,有多少种不同的选法?解:由题意可知,在艺术小组9人中,有且仅有1人既会钢琴又会小号(把该人记为甲),只会钢琴的有6人,只会小号的有2人.把从中选出会钢琴与会小号各1人的方法分为两类.第1类,甲入选,另1人只需从其他8人中任选1人,故这类选法共8种;第2类,甲不入选,则会钢琴的只能从6个只会钢琴的人中选出,有6种不同的选法,会小号的也只能从只会小号的2人中选出,有2种不同的选法,所以这类选法共有6×2=12(种).因此共有8+12=20(种)不同的选法.

大班语言教案:《m, f》教学设计
2.学会声母“b”和单韵母“a”拼读音节的方法。 3.学会拼读“b p m f”与“u、o”组成的音节。 教学难点 掌握拼读声母和韵母组成的音节。 教学过程 一、谈话导入 我们已经认识了韵母家族的6个朋友(出示a o e i u ü)一起读读,你们读得真准,能不能按字母顺序摆一摆,再按顺序读一读。你们记得真清楚。这节课我们一起到拼音王国里再认识四个声母家族的朋友,你们愿意吗? 二、学习“b p m f ”的音形 (一)学习“b”的音形 1.出示“b”的图 (1)引导学生提问:图上的小朋友在干什么? (2)问:这个字母念什么?学生试读“b”。 (3)讲:听广播的“播”读得轻短些,发音时,把两片嘴闭合,把气 憋住,然后突然放开,让气流冲出双唇就是“b”的音。 (4)教师范读。 (5)学生学读,体会发音方法。 (6)开火车读。 2.学习“b”的形 (1)引导学生提问:怎样记住“b”的形?或“b”与图中的哪一部分很像? (2)你们能编一个记忆“b”的小儿歌吗? 拉开天线听广播“b b b”。 右下半圆“b b b”。 6字“b”。…… 3.指导书写b(1)讲:我们先认识一个字母基本笔画:“丨”上竖。 (2)请同学们观察书中字母“b”先写哪笔,再写哪笔,几笔写成?占什么格?同桌同学互相说说。(3)学生说笔顺、位置,教师范写,强调“b”的第一笔在上格的三分之一处起笔到第三条线停笔。 (4)学生书空笔顺。 (5)学生在拼音本上抄字头。教师行间巡视,进行个别辅导。纠正学生的写姿和执笔方法。对姿势正确的学生及时表扬鼓励。

大班语言教案:《i,u,ü》教学设计
2、学会正确认读i、u、ü的带调韵母。知道ü上标声调时,上面的小圆点不写。3、会在四线格里抄写i、u、ü三个单韵母。课时安排:2课时第一课时 教学目标:教学单韵母i、u并抄写。 教学过程: 一、 复习检查。 1、猜谜语。 (1)白鹅倒影是什么韵母? (2)圆脸小姑娘,小辫右边扎。这是什么韵母? (3)像个圆圈是什么韵母? 2、抽读字母卡片。 二、 教学单韵母i。 1、看图说话引出i。 图上画着什么?图上画着一件衣服。i的发音与“衣”的音相同。 2、教学i的发音,认清字形。 (1)发音要领:发音时嘴比发e时开得更小,只留一条小缝,舌前部升高,接近上腭,舌尖抵住下齿背,让气从舌尖和上腭中间自然流出。 (2)教师范读、领读。 (3)记忆字形。 i像什么?顺口溜:“像支蜡烛i、i、i。” 3、书写指导:先写竖,再写点,两笔写成。 三、 教学单韵母u。 1、看图说话引出u。 图上画着什么?“树上有一只乌鸦。”乌鸦的“乌”就是u。 2、教学u的发音,认清字形。 (1)发音要领:发音时把嘴唇收拢,嘴唇比发o时更圆更小,舌尖后缩,舌根抬高,让气从小洞中出来。 (2)教师范读,领读。 (3)记忆字形。 可用顺口溜:“像只茶杯u、u、u。” 3、书写指导:u一笔写成。 四、 巩固复习。

扇形统计图教案教学设计
教学目标1、明确扇形统计图的制作步骤,能够根据相关数据较为准确地制作扇形统计图.2、进一步理解扇形统计图的特点,建立百分比大小和扇形圆心角大小之间初步的直观敏感度.3、能够实现不同统计图数据间的合理转换,再次体会几种统计图的不同特点,为合理选择统计图表示数据打下一定的基础.4、通过实例,理解三种统计图的特点,能根据具体问题选择合适的统计图清晰、有效地描述数据.5、在统计活动的过程中,通过相互间的合作与交流,掌握画统计图和选择统计图的方法;经历数据的收集、整理和简单分析、作出决策的统计活动过程,发展统计观念.6、通过对现实生活中的数据分析,感受数学与现实生活的密切联系,说出统计图在现实生活中的应用,提高学习数学兴趣.

学做家常菜教学设计教案
小学五年级的学生应该具备一些生活技能, 学做家常菜是我们生活的必需,是每个,人都应该掌握的生存技能。本主题的目的通过学习做简单的家常菜,引领小学生走进家务劳动,锻炼生活的自理能力和提高适应生活的能力,体会生活和学习的乐趣,激发学生将学校学习和家务劳动密切结合起来,形成积极的生活和学习的态度。本主题安排了“问题与思考”“学习与探究”“实践与体验”总结与交流“拓展与创新”五个环节,从提出问题开始,到探究与体验,最后到学有所用,循序渐进,引导学习走进中式餐饮文化,学做日常生活中的家常菜,掌握劳动的技能和方法,体验做家务劳动带来的快乐和享受,激发学生对家常菜的探究与实践的兴趣,逐步掌握日常生活所需的基本技能,培养热爱劳动、热爱生活的意识。

数据的整理教案教学设计
一、课前准备师:同学们想一想,你同父母一起去商店买衣服时,衣服上的号码都有哪些,标志是什么?学生:我看到有些衣服上标有M、S、L、XL、XXL等号码.但我不清楚代表的具体范围,适合什么人穿,但肯定与身高、胖瘦有关.师:这位同学很善动脑,也爱观察.S代表最小号,身高在150~155cm的人适合穿S号.M号适合身高在155~160cm的人着装……厂家做衣服订尺寸也并不是按所有人的尺寸定做,而是按某个范围分组批量生产.你觉得这种生产方法有什么优点?学校要为同学们订制校服,为此小明调查了他们班50名同学的身高,结果(单位cm).如下

反比例函数教案教学设计
本节的内容主要是反比例函数的概念教学.反比例函数概念的建立,不能从形式上进行简单的抽象与概括,而是对这些实例从不同角度抽象出本质属性后,再进行概括。教材设计的基本思路是从现实生活中大量的反比例关系中抽象出反比例函数概念,让学生进一步感受函数是反映现实世界中变量关系的一种有效数学模型,逐步从对具体反比例函数的感性认识上升到对抽象的反比例函数概念的理性认识. 同时本节的学习内容,直接关系到本章后续内容的学习,也是继续学习其它各类函数的基础,其中蕴涵的类比、归纳、对应和函数的数学思想方法,对学生今后研究问题、解决问题以及终身的发展都是非常有益的.基于以上分析,本节教学设计是建立在一个个数学活动的基础上,经过对情境理解、本质抽象的积累而形成的.让学生对一类问题情境中两个变量间的关系,在充分经历写表达式,计算函数值和观察函数值随自变量变化规律的过程中,逐步概括形成反比例函数的概念.针对教学实际,我选取了贴学生现实的,有价值的实例“文具店里买学习用品”和“剪面积为定值的长方形纸片”等作为问题情境.

《将进酒》教案教学设计
教师活动 学生活动设计意图 情境导入:教师配乐叙述诗歌创作背景投入倾听 尽可能调动学生情绪诵读入境:“读李诗者于雄快之中得其深远宕逸之神,才是谪仙人面目”(投影展示)教师范读,酝酿情感(播放配乐)1、学生自读感知诗韵 2、学生齐读进入诗境 调动学生积极性,诵读时用自己的情绪感染学生精读涵咏:教师就诗歌内容进行提问,李白怎样喝酒,劝朋友喝酒的方式、原因,他有那些愁并说明理由,并按照自己的理解诵读。教师必要时给出相应的提示。投影展示:人生苦短 怀才不遇 交流研讨诵读 引导学生从诗句入手,疏通诗意,把握情感

李商隐诗两首教学设计教案
我们不妨将主旨放在“庄生晓梦迷蝴蝶,望帝春心托杜鹃。沧海月明珠有泪,蓝田日暖玉生烟。”二联之前,那么,事情就变得简单起来了:华年如庄生晓梦迷蝴蝶;华年如望帝春心托杜鹃;华年如沧海月明珠有泪;华年如蓝田日暖玉生烟。从课下注释,我们很容易就可以看出,这四句每一句都在用典。因此,我们通过对典故的解读,然后加以整理,将其理顺,似乎就可以完成对诗歌内容的解读;至于什么悼亡、爱情,不妨抛之脑后,毕竟,没有那些其他的主题,也并没有让诗歌失色,而加上这些捉摸不定的主题,只是让诗歌增加了所谓的神秘色彩,徒增阅读难度而已。
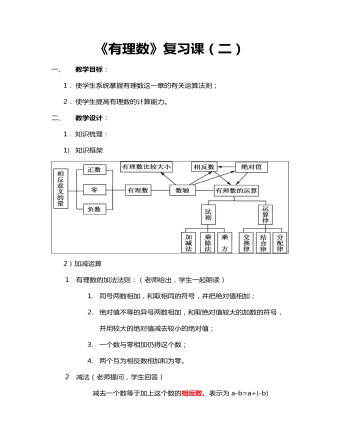
有理数复习教案教学设计
3)乘除运算①有理数的乘法法则:(老师给出,学生一起朗读)1. 两数相乘,同号得正,异号得负,并把绝对值相乘;2. 任何数与零相乘都得零;3. 几个不等于零的数相乘,积的符号由负因数的个数决定,当负因数有奇数个数,积为负;当负因数的个数为偶数个时,积为正;4. 几个有理数相乘,若其中有一个为零,积就为零。②有理数的除法法则:(老师提问,学生回答)1. 两个有理数相除,同号得正,异号得负,并把绝对值相除;2. 除以一个数等于乘以这个数的倒数。③关系(老师给出)除法转化为乘法进行运算。

好玩的磁铁教案教学设计
中班的幼儿开始愿意探究新异的事物或现象来满足自己的好奇心,所以,我们的科学活动设计要在浅显易懂,适合中班幼儿年龄特征的同时,引发幼儿对科学的初步探究能力。中班的幼儿已经具有注意到新异事物或现象的,因此,我们在设计科学活动时要让幼儿充分发挥想象,对磁铁这种“新异”事物提出问题,如什么是磁铁?什么时候看见过磁铁?等等类似的问题,可以增强幼儿的探索兴趣,提高幼儿的探索的积极性,有利于激发幼儿的想象力。 中班幼儿主要以具体形象为主,需要具体的活动场景和活动形式,所以活动设计要提供幼儿合适的情景以提供操作思考的机会,进一步发展幼儿的自主性和主动性。中班幼儿与小班幼儿相比,活动时间也有所增加,因此也需要在活动时间上给予一定的保证。





















