-

人教A版高中数学必修一正弦函数、余弦函数的图像教学设计(2)
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系. 数学学科素养1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.

人教A版高中数学必修一正弦函数、余弦函数的性质教学设计(2)
本节课是正弦函数、余弦函数图像的继续,本课是正弦曲线、余弦曲线这两种曲线的特点得出正弦函数、余弦函数的性质. 课程目标1.了解周期函数与最小正周期的意义;2.了解三角函数的周期性和奇偶性;3.会利用周期性定义和诱导公式求简单三角函数的周期;4.借助图象直观理解正、余弦函数在[0,2π]上的性质(单调性、最值、图象与x轴的交点等);5.能利用性质解决一些简单问题. 数学学科素养1.数学抽象:理解周期函数、周期、最小正周期等的含义; 2.逻辑推理: 求正弦、余弦形函数的单调区间;3.数学运算:利用性质求周期、比较大小、最值、值域及判断奇偶性.4.数学建模:让学生借助数形结合的思想,通过图像探究正、余弦函数的性质.重点:通过正弦曲线、余弦曲线这两种曲线探究正弦函数、余弦函数的性质; 难点:应用正、余弦函数的性质来求含有cosx,sinx的函数的单调性、最值、值域及对称性.

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
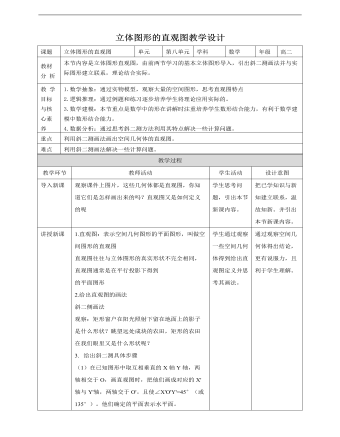
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
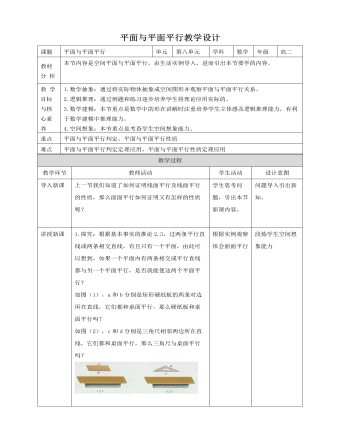
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
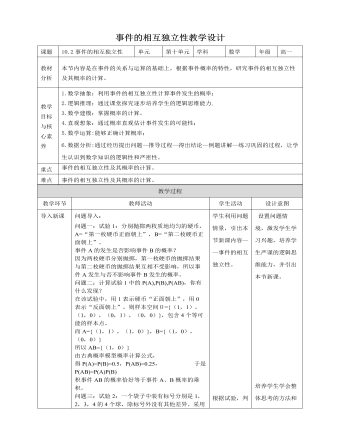
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
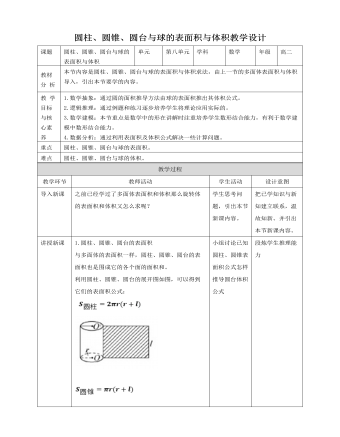
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

高一年级工作总结
重视与家长、社会的联系,构建比较完整的德育教育网络: 本期来,通过周会课、法制与心理健康教育课,对学生进行了针对性的思想教育。年级组、各班根据学生实际情况,通过家访、电话联系等形式,加强教师与家长、学校与家庭、社会的联系,沟通了学校教育和家庭教育。

XX年下半年第一学期国旗下讲话稿
老师、同学们:同学们,今日的习惯,决定明天的你们。因此,在今天的学习生活中,同学们一定要养成一些好的习惯,比如:习惯于主动打扫卫生,形成热爱劳动的习惯;习惯于说声“谢谢”、“你好”、“对不起”,形成以礼待人的好习惯;习惯于每天坚持锻炼,形成健美的体魄;同学交往中习惯于理解、宽容,便能化干戈为玉帛;习惯于去用心观察,才能形成好的观察能力;习惯于提前预习,课后复习,才能形成高效的学习方法……法国学者培根说过,“习惯是人生的主宰,人们应该努力追求好习惯。”是的,行为习惯就像我们身上的指南针,指引着我们的行动。爱因斯坦有句名言,“一个人取得的成绩往往取决于性格上的伟大。”而构成性格的,正是日常生活中的一个个好习惯。好习惯养成得越多,个人的能力就越强。养成好的习惯,就如同为梦想插上了翅膀,它将为人生的成功打下坚定的基石。小时候的 鲁迅 先生,就养成了不迟到的习惯,他要求自己抓紧时间,时刻叮嘱自己凡事都要早做。这位以“小跑走完一生”的作家,在中国文学史上留下了辉煌的业绩。可见,行为习惯对一个人各方面的素质起了决定性的作用。

5月份国旗下讲话稿:净化语言,美化校园
今天,我要给大家聊聊美化校园的话题。我想现在可能会有一些同学在想,美化校园?我们的校园不是很美吗?你看校园里:操场上干干净净无纸屑,四周围绿树草皮话烂漫,楼房整齐一排排,同学们穿红着绿好漂亮,外面还有绿水青山来拥抱,谁敢说我们的校园不美吗啊?可是今天,我要实话实说:我们的校园里还有美中的不足,还存在着“丑”的东西。那么这个“丑”到底藏在哪里呢?我说这个“丑”就藏在一些同学的嘴巴里。前些天,我路过教室门口,竟听到有同学在相互传唱这样的一首打油诗:读书苦啊,读书累,读书还要缴学费,不如参加黑社会,有吃有喝有地位下面还有更难听的,我也不好意思给大家再背下去了。当时,我心情沉重地回到了教室坐在坐位上想,跟同学聊起这样的事情。同学们在笑着告诉我,前些时候还流传过这样一个顺口溜:一年级是小偷二年级是贼,三年级的美女没人追,四年级的帅哥排成对,五年级的情书满天飞,六年级的鸳鸯成双对。

9月1日国旗下新学期寄语讲话范例
同学们,作为莘莘学子,你们首先要珍惜宝贵的学习机会和大好的青春时光,从点滴做起,专心致志、争取以优异成绩回报父母、回报学校。当今社会的竞争主流是知识和人才的竞争,如果不接受良好的教育,没有丰富的知识,就难以在未来的高科技社会中立足,更谈不上报答父母,奉献社会了。所以你们要端正学习态度,积极主动地学习,发扬顽强拼搏、不怕困难、敢于竞争的精神,勤于思考、善于总结、学会学习、学会创造,为进一步提高学习成绩而努力。还有,你们要继续发扬遵规守纪的良好习惯,严格遵守《小学生日常行为规范》和学校的管理制度,加强责任感,不断规范自身的言行,学会做人,学会合作,及早成为一名具有品格高尚、人格健全、志向远大的优秀学生。老师们、同学们,新的学期里,我希望每位老师、每位同学都能继续发扬过去认真工作、努力学习的良好作风,谦虚谨慎、锐意进取,共同携手,为开创银滩镇中心小学的美好明天而共同努力!祝老师们在新学期里工作顺利、精神愉快!祝同学们学习进步、健康成长。

国旗下的讲话—语言美,春风化雨润心田
尊敬的校领导、老师、同学们:今天我在这庄严的五星红旗下,代表121班讲话,我今天所讲的题目是《语言美,春风化雨润心田》。说话文明,举止文雅,是中华民族的传统美德。一个人,如果能够出口成章,滔滔不绝,语重心长又能催人奋发,就不仅展示了他深厚的文化功底,更体现了他高尚的品德素养。一句温暖的话语,一个体贴的眼神,看似微不足道,实则意义深远。孔子曾说过不学礼,无以立。我国是一个有着悠久历史的文明古国,具有礼仪之邦的美称。文明礼貌并非是个人生活的小事,而是一个国家社会风尚的真实反映,是一个民族道德素质水平和精神文明程度的标志.每个人从他来到这个世界的那一刻起,就需要别人的爱抚、安慰、体谅、关怀和相互帮助,都渴望真诚友情和相互帮助.当我们快乐时,需要和别人分享,有痛苦烦恼时,需要向别人倾诉

贵州瞳人语影视传媒有限公司保密协议
甲方: 贵州瞳人语影视传媒有限公司 法人签字: 乙方:____________________________ 身份证号码: 双方确认,乙方在甲方任职期间,因工作需要接触到任何材料,除工作需要外,都不得对材料进行复印、拷贝,或以其他形式对外发送。未经公司确认,不得将任何材料向第三方提供,所有工作要遵循公司保密制度进行。第一条:知识产权归属双方确认,乙方在甲方任职期间,因履行职务或者主要是利用甲方的物质技术条件、业务信息等产生的发明创造、作品、计算机软件、技术秘密或其他商业秘密信息,有关的知识产权均属于甲方所有。甲方可以在其业务范围内充分自由地利用这些发明创造、作品、计算机软件、技术秘密或其他商业秘密信息,进行生产、经营或者向第三方转让。乙方应当依甲方的要求,提供一切必要的信息和采取一切必要的行动,包括申请、注册、登记等,协助甲方取得和行使有关的知识产权。

企业年会方案策划方案
20:00 20:05:川剧变脸神奇的蜀中绝技,几百年的中华艺术瑰宝,让您身历其境的体会传统艺术源远流长,亘古不灭的艺术魅力。三个人同时在舞台上演绎变脸绝活更为精彩,在舞台下面和观众零距离接触,体验变脸的魅力。(男1人)

(小学)国旗下讲话:校园卫生,人人有责
今天我国旗下讲话的题目是——校园卫生 人人有责。学校是育人的摇篮,是一方纯净的沃土,然而我们的校园中常常出现一些不和谐的现象。清晨我们到校的第一件事情就是打扫卫生,同学们可能在想:为什么天天打扫天天脏?怎么总有扫不完的垃圾?其实我们每天都在打扫卫生,应该说学校里除了落叶外应该不会再有其他的杂物。可事实不是这样,刚刚扫完的操场、楼梯、教室、走廊一会儿又有新的杂物出现,这些杂物是怎么来的呢?原因很简单,同学们乱扔的。同学们,如果让你们选择,你是愿意在一个脏乱的校园还是愿意在一个整洁的校园里学习?相信大家一定愿意在整洁优美的环境中学习、生活。因为鸟语花香,一尘不染的环境,能让我们拥有美好的心情,学习效率也自然会提高。

