-

人教版高中政治必修3文化创新的源泉和作用精品教案
一、教材分析本节内容主要讲述了社会实践在文化创新中的作用和意义,明确了社会实践是文化创新的源泉,也是文化创新的动力,文化创新的作用,既表现为不断推动社会实践的发展,又表现为不断促进民族文化的繁荣。我们要从中体会社会实践的重要性和意义。二、教学目标(一)知识目标(1) 理解文化发展的实质在于创新;理解社会实践是文化创新的源泉(2) 理解文化创新的作用;理解人民群众是社会实践的主体、文化创新的主体。(二)能力目标培养学生列举实例说明社会实践在 文化创新中的作用。情感、态度价值观目标:帮助学生充分认识建 设社会主义先进文化的意义,增强民族文化的自豪感。 (三)情感、态度与价值观目标情感、态度及价值观目标:通过学习本课题内容,初步理解文化创新的、意义、作用,做一个有“文化”的人,认识到文化创新的重要性。深刻理解建。

人教版高中政治必修3文化与经济、政治精品教案
一、教材分析《文化与经济、政治》是人教版高中政治必修三——文化生活第一单元第一课第二框的教学内容,本课主要评述文化生活对人们交往方式、思维方式和生产方式的影响,说明现代社会中文化与经济、政治相互交融的意义。二、教学目标(一)知识目标◇理解:文化与经济、政治的关系:经济、政治决定文化,文化对经济、政治有重大影响,文化与经济、政治相互交融 ◇分析:经济和政治决定文化,文化是一定经济和政治的反映;文 化对经济发展具有重要作用,文化是生产力;文化对政治文明建设的推动作用及对公民政治素质和权利意识的作;文化日益成为综合国力的重要标志。(二)能力目标通过分析文化与经济、政治的关系,培养辩证分析能力(三)情感、态度、值观目标懂得文化在综合国力竞争中的地位和作用,努力学习将来为增强综合国力贡献力量

人教版高中政治必修3文化塑造人生精品教案
A.人创造了文化,文化创B.人创造了文化,文化也塑造着人,不断丰富着人的精神世界C.文化具有潜移默化的作用D.世界观、人生观、价值观是人们文化素养的核心和标志2、在我国全面建设小康社会的过程中,我们要把民族精神教育纳入国民教育全过程,纳入精神文明建设全过程,使全体人民始终保持昂扬向上的精神状态。这是由于()A.文化能够丰富人的精神世界B.文化能够增强人的精神力量C.文化能够促进人的全面发展D.人的思想意识对事物发展起决定作用3、我国已进入全面建设小康社会,加快推进社会主义现代化的新的发展阶段,人们的温饱问题基本解决,健康有了基本保障。随着物质生活需要逐步得到满足,人们更加注重精神生活需要的满足,对文化活动表现出日渐浓厚的兴趣,文化消费在生活消费中的比重越来越大。这段话主要说明的是,新时期:

新人教版高中英语必修1Unit 1 Teenage Life-Listening and Speaking & Listening and Talking教案
Step 2 Listening and Talking1. The teacher is advised to talk with their new students about the related topic: Boys and girls, do you know some structures to talk about future activities? Talking about future activitiesWe’ll …I plan to …There’ll be …I hope to …We’re going to …2. After their small talk, the teacher can move on by playing the listening and solve the following task.Underline the expressions in the sentences below Cao Jing and Max use to talk about the future.We’ll learn useful skills.I plan to improve my spoken English.There’ll be students from different schools.I hope to make new friends.We’ll talk about teenage life.I’ll learn to make a fire.There’ll be students from different countries at the camp.There’ll be some experts there to show us how to live in the wild.We’re going to learn about wildlife.I’m going to give a speech.I think I’m going to enjoy the activities.I think we’ll have a lot of fun.3. Work in groups. Plan a youth camp.Teacher make the Ss think of ideas for the camp. And they can use the questions below to get started. And have the Ss present their ideas for a youth camp to the class.●What kind of camp is it?●Who will be there?●What will they do?●What will they learn?

新人教版高中英语必修1Unit 2 Travelling Around-Listening and Speaking & Listening and Talking教案
【教学目标与核心素养】1. Instruct students to get main facts by listening and motivate them to talk about the topics about how to prepare for the trip and make reservations by listening and ultimately can make travel arrangements and reservations. 2. Develop students’ sense of cooperative learning and individual thinking capability. 3. Develop students’ different listening skills to solve different listening comprehensive problems.4. Help students to understand how to use the structures “the present continuous tense (be doing) is used to express future plans.【教学重难点】1. Teach students how to focus on key words, not on single words or grammar.2. Prompt Ss to talk about the related topics, such as how to prepare for the trip and make a travel plan.【教学过程】Step 1: Listening and SpeakingLead inThe teacher is advised to talk with their students about the places that they want to travel most both at home and abroad: boys and girls, if you have a chance to travel around the world, where will you go? After their small talk, the teacher can move on by finishing the following listening task:Before travelling, what do we need to prepare for the trip?

新人教版高中英语必修1Unit 3 Sports and Fitness-Listening and Speaking & Listening and Talking教案
Finally, after finishing the task above, the teacher is expected to instruct students to work in groups to finish the following project:Speaking ProjectWhat event or activity would you like to invite your friend to? Make a conversation with a partner.Ski Race: Zhangjiakou, a beautiful city in northern China, will host the Youth Ski Race in December.Track Meet: a great event for track –and –field lovers on 26 October.Gym Class: come and work out at a gym! You can make it.Part 2: Listening and Talking:The teacher is advised to talk with their new students about the related topic: Boys and girls , what do you think of sportsmanship? Let’s listen and find out:Play the listening and match each opinion with the right speaker. Who do you agree with? Why?Cao Jing _____________ Lily _____________ Max _____________A. An athlete should do his/her best to win.B. The girl should stop and help the other girl. Good sportsmanship is more important than wining!C. An athlete should think about honor and his/her fans if he/she is competing for his/her country.Listen again and circle the expressions that you hear in the conversation.

新人教版高中英语必修1Unit 3 Sports and Fitness- Discovering Useful Structures—tag questions教案
【教材分析】This teaching period mainly deals with the grammar: tag questions.This period carries a considerable significance to the cultivation of students’ spoken English. The teacher is expected to enable students to master this period thoroughly and consolidate the knowledge by doing some exercise of good quality.【教学目标与核心素养】1. Get students to have a good understanding of the basic usages of tag questions.2. Enable students to use the basic phrases structures flexibly.3. Develop students’ speaking and cooperating abilities.4. Strengthen students’ great interest in grammar learning.【教学重难点】1. How to enable students to have a good understanding of the basic usages of tag questions.2. How to enable students to use the basic usages of tag questions flexibly.【教学过程】Step1: 语法自主探究一、基本组成方法1.肯定式陈述部分+否定附加疑问部分(前肯后否) You often play badminton, don’t you? 你经常打羽毛球,是吗?You are going to the gym with me, aren’t you?你要和我一起去健身房,是吗?She’s been to shanghai before, hasn’t she? 她以前去过上海,是吗?2.否定式陈述部分+肯定附加疑问部分(前否后肯) It isn't a beautiful flower, is it? 那不是美丽的花,是吗?You didn't go skating yesterday, did you? 你昨天没去滑冰,是吗?They can’t finish it by Friday, can they?他们不能在星期五之前完成,是吗?
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。

人教A版高中数学必修一集合的基本运算教学设计(1)
本节是新人教A版高中数学必修1第1章第1节第3部分的内容。在此之前,学生已学习了集合的含义以及集合与集合之间的基本关系,这为学习本节内容打下了基础。本节内容主要介绍集合的基本运算一并集、交集、补集。是对集合基木知识的深入研究。在此,通过适当的问题情境,使学生感受、认识并掌握集合的三种基本运算。本节内容是函数、方程、不等式的基础,在教材中起着承上启下的作用。本节内容是高中数学的主要内容,也是高考的对象,在实践中应用广泛,是高中学生必须掌握的重点。A.理解两个集合的并集与交集的含义,会求简单集合的交、并运算;B.理解补集的含义,会求给定子集的补集;C.能使用 图表示集合的关系及运算。 1.数学抽象:集合交集、并集、补集的含义;2.数学运算:集合的运算;3.直观想象:用 图、数轴表示集合的关系及运算。
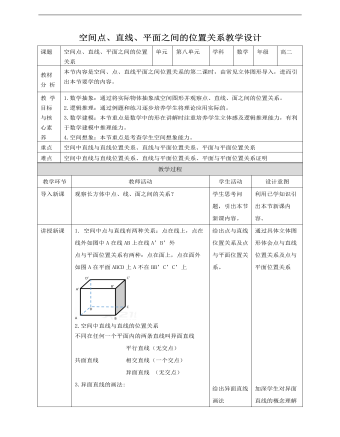
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.

人教A版高中数学必修一正弦函数、余弦函数的图像教学设计(2)
由于三角函数是刻画周期变化现象的数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,我们只要认识清楚它在一个周期的区间上的性质,那么它的性质也就完全清楚了,因此本节课利用单位圆中的三角函数的定义、三角函数值之间的内在联系性等来作图,从画出的图形中观察得出五个关键点,得到“五点法”画正弦函数、余弦函数的简图.课程目标1.掌握“五点法”画正弦曲线和余弦曲线的步骤和方法,能用“五点法”作出简单的正弦、余弦曲线.2.理解正弦曲线与余弦曲线之间的联系. 数学学科素养1.数学抽象:正弦曲线与余弦曲线的概念; 2.逻辑推理:正弦曲线与余弦曲线的联系; 3.直观想象:正弦函数余弦函数的图像; 4.数学运算:五点作图; 5.数学建模:通过正弦、余弦图象图像,解决不等式问题及零点问题,这正是数形结合思想方法的应用.
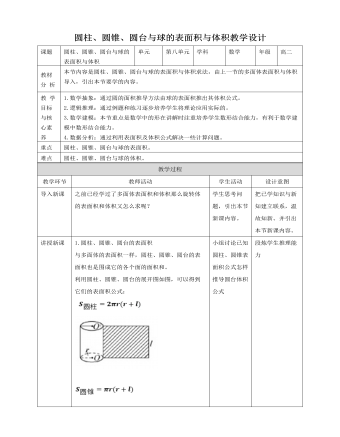
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
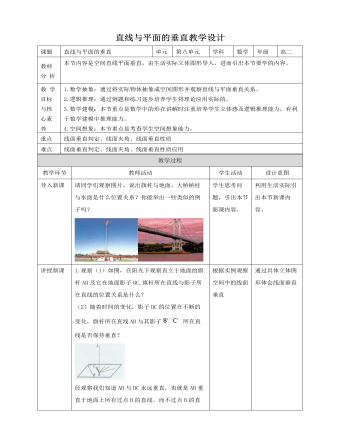
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
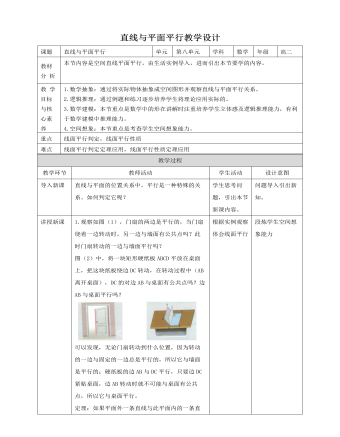
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
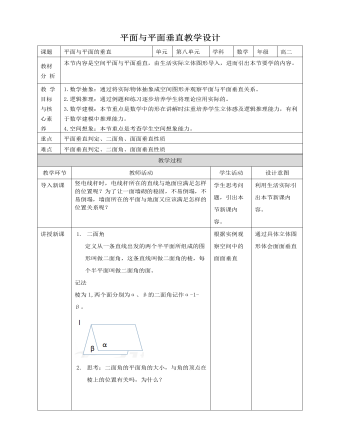
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?

人教A版高中数学必修一三角函数的应用教学设计(2)
本节课是在学习了三角函数图象和性质的前提下来学习三角函数模型的简单应用,进一步突出函数来源于生活应用于生活的思想,让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力.课程目标1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.2.实际问题抽象为三角函数模型. 数学学科素养1.逻辑抽象:实际问题抽象为三角函数模型问题;2.数据分析:分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立数学模型; 3.数学运算:实际问题求解; 4.数学建模:体验一些具有周期性变化规律的实际问题的数学建模思想,提高学生的建模、分析问题、数形结合、抽象概括等能力.
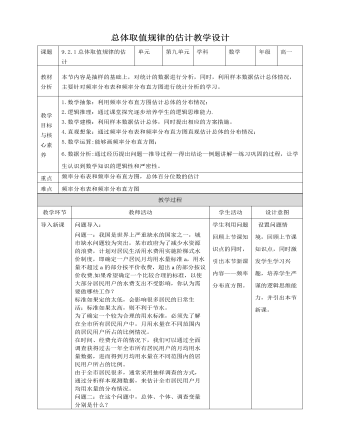
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。

人教A版高中数学必修一函数模型的应用教学设计(2)
本节通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用,进一步认识到函数是描述客观世界变化规律的基本数学模型,能初步运用函数思想解决一些生活中的简单问题。课程目标1.能利用已知函数模型求解实际问题.2.能自建确定性函数模型解决实际问题.数学学科素养1.数学抽象:建立函数模型,把实际应用问题转化为数学问题;2.逻辑推理:通过数据分析,确定合适的函数模型;3.数学运算:解答数学问题,求得结果;4.数据分析:把数学结果转译成具体问题的结论,做出解答;5.数学建模:借助函数模型,利用函数的思想解决现实生活中的实际问题.重点:利用函数模型解决实际问题;难点:数模型的构造与对数据的处理.

