-

北师大初中数学九年级上册用公式法求解一元二次方程1教案
∴(-2m a)2-4(b+c)(c-b)m=0,即4m(a2+b2-c2)=0.又∵m≠0,∴a2+b2-c2=0,即a2+b2=c2.根据勾股定理的逆定理可知△ABC为直角三角形.方法总结:根据一元二次方程根的情况,利用判别式得到关于一元二次方程系数的等式或不等式,再结合其他条件解题.三、板书设计用公式法解一元二次方程求根公式:x=-b±b2-4ac2a(a≠0,b2-4ac≥0)用公式法解一元二次 方程的一般步骤①化为一般形式②确定a,b,c的值③求出b2-4ac④利用求根公式求解一元二次方程根的判别式经历从用配方法解数字系数的一元二次方程到解字母系数的一元二次方程,探索求根公式,发展学生合情合理的推理能力,并认识到配方法是理解求根公式的基础.通过对求根公式的推导,认识到一元二次方程的求根公式适用于所有的一元二次方程,操作简单.体会数式通性,感受数学的严谨性和数学结论的确定性.提高学生的运算能力,并养成良好的运算习惯.

北师大初中数学九年级上册一元二次方程的解及其估算1教案
首先列表,利用未知数的取值,根据一元二次方程的一般形式ax2+bx+c=0(a,b,c为常数,a≠0)分别计算ax2+bx+c的值,在表中找到使ax2+bx+c可能等于0的未知数的大致取值范围,然后再进一步在这个范围内取值,逐步缩小范围,直到所要求的精确度为止.(2)在估计一元二次方程根的取值范围时,当ax2+bx+c(a≠0)的值由正变负或由负变正时,x的取值范围很重要,因为只有在这个范围内,才能存在使ax2+bx+c=0成立的x的值,即方程的根.三、板书设计一元二次方程的解的估算,采用“夹逼法”:(1)先根据实际问题确定其解的大致范围;(2)再通过列表,具体计算,进行两边“夹逼”,逐步获得其近似解.“估算”在求解实际生活中一些较为复杂的方程时应用广泛.在本节课中让学生体会用“夹逼”的思想解决一元二次方程的解或近似解的方法.教学设计上,强调自主学习,注重合作交流,在探究过程中获得数学活动的经验,提高探究、发现和创新的能力.

北师大初中数学九年级上册一元二次方程的根与系数的关系2教案
3、一般地,对于关于 方程 为已知常数, ,试用求根公式求出它的两个解x1、x2,算一算x1+x2、x1?x2的值,你能得出什么结果?与上面发现的现象是否一致。【知识应用】 1、(1)不解方程,求方程两根的和两根的积:① ② (2)已知方程 的一个根是2,求它的另一个根及 的值。(3)不解方程,求一 元二次方程 两个根的①平方和;②倒数和。(4)求一元二次方程,使它的两个根是 。【归纳小结】【作业】1、已知方程 的一个根是1,求它的另一个根及 的值。2、设 是方程 的两个根,不解方程,求下列各式的值。① ;② 3、求一个一元次方程,使它的两 个根分别为:① ;② 4、下列方程两根的和与两根的积各是多少 ?① ; ② ; ③ ; ④ ;

北师大初中数学九年级上册用公式法求解一元二次方程2教案
二、填空题1.一元二次方程ax2+bx+c=0(a≠0)的求根公式是________,条件是________.2.当x=______时,代数式x2-8x+12的值是-4.3.若关于x的一元二次方程(m-1)x2+x+m2+2m-3=0有一根为0,则m的值是_____.三、综合提高题1.用公式法解关于x的方程:x2-2ax-b2+a2=0.2.设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,(1)试推导x1+x2=- ,x1·x2= ;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.3.某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时 元收费.(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)(2)下表是这户居民3月、4月的用电情况和交费情况

北师大初中数学九年级上册用频率估计概率1教案
(2)假如你摸一次,估计你摸到白球的概率P(白球)=;(3)试估算盒子里黑球有多少个.解:(1)0.6(2)0.6(3)设黑球有x个,则2424+x=0.6,解得x=16.经检验,x=16是方程的解且符合题意.所以盒子里有黑球16个.方法总结:本题主要考查用频率估计概率的方法,当摸球次数增多时,摸到白球的频率mn将会接近一个数值,则可把这个数值近似看作概率,知道了概率就能估算盒子里黑球有多少个.三、板书设计用频率估计概率用频率估计概率用替代物模拟试验估计概率通过实验,理解当实验次数较大时实验频率稳定于理论频率,并据此估计某一事件发生的概率.经历实验、统计等活动过程,进一步发展学生合作交流的意识和能力.通过动手实验和课堂交流,进一步培养学生收集、描述、分析数据的技能,提高数学交流水平,发展探索、合作的精神.
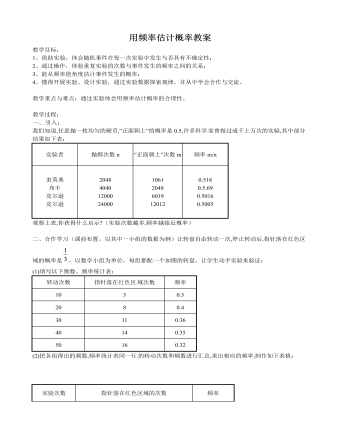
北师大初中数学九年级上册用频率估计概率2教案
(1)填写表格中次品的概率.(2)从这批西装中任选一套是次品的概率是多少?(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装?六、课堂小结:尽管随机事件在每次实验中发生与否具有不确定性,但只要保持实验条件不变,那么这一事件出现的频率就会随着实验次数的增大而趋于稳定,这个稳定值就可以作为该事件发生概率的估计值。七、作业:课后练习补充:一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球与10的比值,再把球放回袋中摇匀。不断重复上述过程5次,得到的白求数与10的比值分别为:0.4,0.1,0.2,0.1,0.2。根据上述数据,小亮可估计口袋中大约有 48 个黑球。

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册用树状图或表格求概率1教案
由上表可知,共有6种结果,且每种结果是等可能的,其中两次摸出白球的结果有2种,所以P(两次摸出的球都是白球)=26=13;(2)列表如下:由上表可知,共有9种结果,且每种结果是等可能的,其中两次摸出白球的结果有4种,所以P(两次摸出的球都是白球)=49.方法总结:在试验中,常出现“放回”和“不放回”两种情况,即是否重复进行的事件,在求概率时要正确区分,如利用列表法求概率时,不重复在列表中有空格,重复在列表中则不会出现空格.三、板书设计用树状图或表格求概率画树状图法列表法通过与学生现实生活相联系的游戏为载体,培养学生建立概率模型的思想意识.在活动中进一步发展学生的合作交流意识,提高学生对所研究问题的反思和拓展的能力,逐步形成良好的反思意识.鼓励学生思维的多样性,发展学生的创新意识.

北师大初中数学九年级上册用公式法求解一元二次方程2教案
二、填空题1.一元二次方程ax2+bx+c=0(a≠0)的求根公式是________,条件是________.2.当x=______时,代数式x2-8x+12的值是-4.3.若关于x的一元二次方程(m-1)x2+x+m2+2m-3=0有一根为0,则m的值是_____.三、综合提高题1.用公式法解关于x的方程:x2-2ax-b2+a2=0.2.设x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,(1)试推导x1+x2=- ,x1·x2= ;(2)求代数式a(x13+x23)+b(x12+x22)+c(x1+x2)的值.3.某电厂规定:该厂家属区的每户居民一个月用电量不超过A千瓦时,那么这户居民这个月只交10元电费,如果超过A千瓦时,那么这个月除了交10元用电费外超过部分还要按每千瓦时 元收费.(1)若某户2月份用电90千瓦时,超过规定A千瓦时,则超过部分电费为多少元?(用A表示)(2)下表是这户居民3月、4月的用电情况和交费情况

北师大初中数学九年级上册正方形的判定1教案
∴OE=OF=OG=OH.又∵EG⊥FH,∴四边形EFGH为菱形.∵EO+GO=FO+HO,即EG=HF,∴四边形EFGH为正方形.方法总结:对角线互相垂直平分且相等的四边形是正方形.探究点二:正方形、菱形、矩形与平行四边形之间的关系填空:(1)对角线________________的四边形是矩形;(2)对角线____________的平行四边形是矩形;(3)对角线__________的平行四边形是正方形;(4)对角线________________的矩形是正方形;(5)对角线________________的菱形是正方形.解:(1)相等且互相平分(2)相等(3)垂直且相等(4)垂直(5)相等方法总结:从对角线上分析特殊四边形之间的关系应充分考虑特殊四边形的性质与判别,防止混淆.菱形、矩形、正方形都是平行四边形,且是特殊的平行四边形,特殊之处在于:矩形是有一个角为直角的平行四边形;菱形是有一组邻边相等的平行四边形;而正方形是兼具两者特性的更特殊的平行四边形,它既是矩形,又是菱形.

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中数学九年级上册用公式法求解一元二次方程1教案
易错提醒:利用b2-4ac判断一元二次方程根的情况时,容易忽略二次项系数不能等于0这一条件,本题中容易误选A.【类型三】 根的判别式与三角形的综合应用已知a,b,c分别是△ABC的三边长,当m>0时,关于x的一元二次方程c(x2+m)+b(x2-m)-2m ax=0有两个相等的实数根,请判断△ABC的形状.解析:先将方程转化为一般形式,再根据根的判别式确定a,b,c之间的关系,即可判定△ABC的形状.解:将原方程转化为一般形式,得(b+c)x2-2m ax+(c-b)m=0.∵原方程有两个相等的实数根,∴(-2m a)2-4(b+c)(c-b)m=0,即4m(a2+b2-c2)=0.又∵m≠0,∴a2+b2-c2=0,即a2+b2=c2.根据勾股定理的逆定理可知△ABC为直角三角形.方法总结:根据一元二次方程根的情况,利用判别式得到关于一元二次方程系数的等式或不等式,再结合其他条件解题.

北师大初中数学九年级上册一元二次方程的根与系数的关系2教案
2、猜想 一元二次方程的两个根 的和与积和原来的方程有什么联系?小组交流。3、一般地,对于关于 方程 为已知常数, ,试用求根公式求出它的两个解x1、x2,算一算x1+x2、x1?x2的值,你能得出什么结果?与上面发现的现象是否一致。【知识应用】 1、(1)不解方程,求方程两根的和两根的积:① ② (2)已知方程 的一个根是2,求它的另一个根及 的值。(3)不解方程,求一 元二次方程 两个根的①平方和;②倒数和。(4)求一元二次方程,使它的两个根是 。【归纳小结】【作业】1、已知方程 的一个根是1,求它的另一个根及 的值。2、设 是方程 的两个根,不解方程,求下列各式的值。① ;② 3、求一个一元次方程,使它的两 个根分别为:① ;② 4、下列方程两根的和与两根的积各是多少 ?① ; ② ; ③ ; ④ ;

政协关于食品安全工作情况调研报告
一、我县食品安全工作基本情况全县现有食品生产企业4户(均获得食品安全市场准入资格),产品涉及4大类15个品种,食品加工小作坊16户;各类食品流通经营户342户(企业14户,个体工商户328户);各类餐饮单位165户(小型餐饮单位125户);餐具消毒包装企业1户;农药、兽药经销点29户,生猪屠宰场、加工点4个;农贸市场1处。近年来,我县食品安全工作在县委、县政府的高度重视和正确领导下,认真贯彻落实《食品安全法》,立足本县实际,科学谋划工作思路,强化组织领导,保障经费投入,在食品安全委员会各成员单位的不懈努力下,全县食品生产经营秩序渐趋规范,食品安全保障水平明显提升,未发生过大的安全事故。

移风易俗工作开展情况调研报告
推动移风易俗,是功在当代、利在千秋的大事,是惠泽万家、弘扬新风的好事。回顾近年来XX市推动移风易俗工作过程,能够深切感受到移风易俗工作虽然荆棘载途,但同时也民心所向:困难在于一些传统观念历史悠久,已存在成百甚至上千年,在农村根深蒂固;移风易俗涉及面广,XX全市范围内或多或少都存在陈规陋习现象;相关的宣传教育还不够深入,整治标准不明且操作性不强,不具备强制性。同时也要清醒地看到,XX市的XX县、XX县、XX县等县区已经有了良好的移风易俗实践探索基础,且长期以来人民群众对婚丧嫁娶礼金早已不堪重负,拥有强烈的改革意愿。正是基于这些问题的存在和影响,XX市《意见》的出台可谓正当其时、势在必行,具有很强的针对性和必要性。

我市精神文明建设工作调研报告三篇
(一) 城乡居民素质明显提高。多年来,我县认真贯彻《公民道德建设实施纲要》,坚持不懈开展公民道德实践活动,收到了良好的效果,促进了城乡居民文明素质的提高。公共场所乱扔垃圾、随地吐痰、乱贴乱画、乱闯红灯、候车不排队等不文明现象明显减少。涌现出了许多先进典型,无不成为精神文明建设的良好教材和先进楷模,激发了我县人民建设文明汶川的热情和动力。 (二) 人文环境更加优化。一是文化氛围日益浓厚,行业服务更加规范。目前,全县大多数行业和窗口广泛开展了优质服务竞赛活动,并且形成了富有个性、特色鲜明的文明品牌,服务水平不断提升。二是政务环境更加透明。通过实施“阳光工程”,实行政府信息公开、新闻发布会、重大社会公共事项决策听证等制度,政府工作透明度不断增强。通过实行“放权提速”,实施“政府上网工程”,实行“窗口式办公”、“一站式服务”,进一步提高了政府效能。

我市精神文明建设工作调研报告三篇
(一) 城乡居民素质明显提高。多年来,我县认真贯彻《公民道德建设实施纲要》,坚持不懈开展公民道德实践活动,收到了良好的效果,促进了城乡居民文明素质的提高。公共场所乱扔垃圾、随地吐痰、乱贴乱画、乱闯红灯、候车不排队等不文明现象明显减少。涌现出了许多先进典型,无不成为精神文明建设的良好教材和先进楷模,激发了我县人民建设文明汶川的热情和动力。 (二) 人文环境更加优化。一是文化氛围日益浓厚,行业服务更加规范。目前,全县大多数行业和窗口广泛开展了优质服务竞赛活动,并且形成了富有个性、特色鲜明的文明品牌,服务水平不断提升。二是政务环境更加透明。通过实施“阳光工程”,实行政府信息公开、新闻发布会、重大社会公共事项决策听证等制度,政府工作透明度不断增强。通过实行“放权提速”,实施“政府上网工程”,实行“窗口式办公”、“一站式服务”,进一步提高了政府效能。

工作调研报告:“大众创业、万众创新”
二是规划引导。科学规划是创新创业的重要前提,衡阳县委县政府把规划编制工作纳入重要议事日程。加强基地规划。精心规划高新技术企业创新创业孵化基地、互联网企业创新创业孵化基地和电子信息企业创新创业孵化基地,通过规划来拓宽创新创业空间。加紧产业规划。按照“1163”产业布局,重点发展生物医药、先进装备制造、电子信息三大产业。界牌陶瓷循环经济产业园以瓷泥精深加工为入口,带动工业陶瓷、特种陶瓷、礼品陶瓷、日用陶瓷等高端陶瓷产业发展。发展西渡都市型产业、关市铁矿采选、井头石材开采及加工、演陂建材产业、库宗桥拆装家具、高端红木家具等木器加工产业集聚区。通过规划引导广大民众选准创业领域、选对创业合伙人。

农业农村工作情况调研报告三篇
1、特色产业稳步发展。以发展现代休闲农业为主题,引导群众积极调整种植结构,大力发展特色农业、效益农业、节水设施农业,形成了以农家乐为主的特色产业。 2、农业产业标准化体系日渐完善。以基地为依托,以市场为导向,着力培育和发展大场大户,推动区域内主导产业的优化升级,以狮山茶场客家风情园为代表,实行合作社+基地+农户的产业经营模式生产,带动了周边xx多农户发展现代农业,直接解决了xxx多人的就业问题。xx年引进茶叶新品种黄金芽等优良品种在xx分场建立高产示范基地,目前基地面积xxx亩。

农村环境整治工作情况的调研报告
(一)大力开展生活垃圾治理设施建设,垃圾收运系统进一步完善近年来,我市着力健全垃圾收集处置系统建设,通过招商引资引进广西鸿生源环保科技有限公司,投资1.2亿元,启动日处理200吨生活垃圾无害化处理项目。为减少原有垃圾填埋场对周围环境的影响,投入500万元对原垃圾填埋场进行封场处理。投资3500万元,完成XX市城乡生活垃圾收运系统工程建设,建成垃圾压缩中转站14座(其中城区2座、乡镇12座),配置转运车10台、勾臂式垃圾车48台、可卸式垃圾箱600个。积极探索乡镇生活垃圾源头处理模式,投资66.88万元,采购“分散式生活垃圾处理站”设备2台,在石堡乡、葫市镇开展生活垃圾就地处理试点工作,采购垃圾箱125个、垃圾钩臂车9辆,并分配至各乡镇、村,进一步提升了农村生活垃圾收运能力。目前,我市生活垃圾收运设施覆盖全市17个乡镇(街道)和79个行政村,乡(镇)覆盖率100%,城乡生活垃圾无害化处理率90%以上。

