-

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
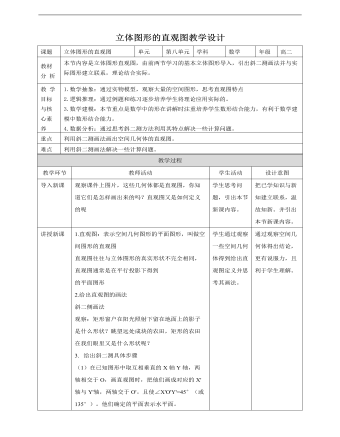
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
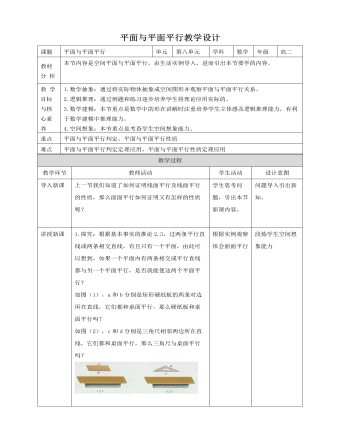
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
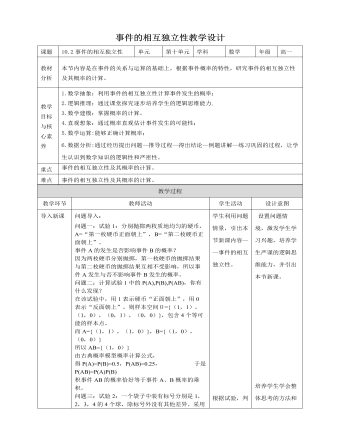
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
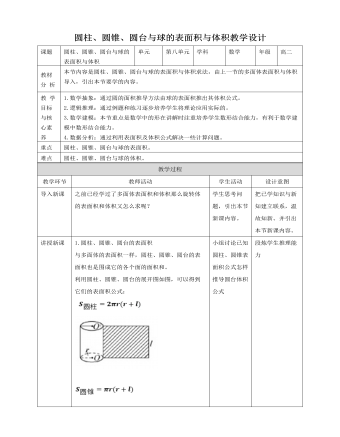
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
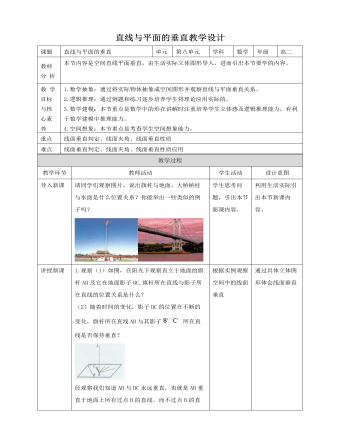
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
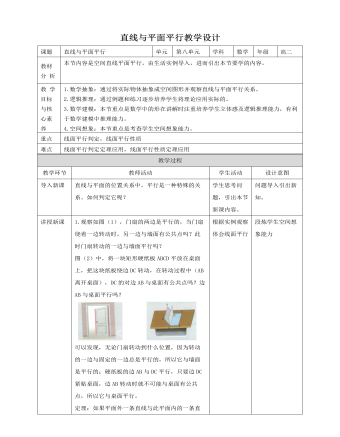
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

上海离婚协议书
妻婚后购有坐落在____路____号的楼房一套,合同价人民币万元,现值人民币万元(包括房内装修内附属设施)。购房时以男方为主贷人贷款42万元,现尚剩余贷款本金30万元。该房购买时首付18万元,首付款来源于婚后双方存款。现协商该套房产归女方所有,由女方给付男方房屋折价款35万元,折价款计算公式为:房屋现价100万元-未还贷款本金30万元/2。女方给付男方的折价款35万元在两年内分3次付清

上海销售合同
甲方向乙方出售的车辆,其质量必须符合国家汽车产品标准或行业标准,并符合出厂检验标准,符合安全驾驶和说明书载明的基本使用要求,符合车辆落籍地政府关于尾气排放的标准。

上课了 说课稿
《上课了》是统编《道德与法治》一年级上册第二单元第8课,经过了第一单元的学习,学生已经能够初步适应新环境,结交了新同学,对老师有了更多的接纳和了解。安全意识有所增强。正在更深地融入学校的生活和学习当中。本单元主要从校园的样貌、规则引导学生建立规则意识和对学习和课堂上下的活动建立亲近感。第8课《上课了》旨在引导学生建立良好的学习准备、课堂参与的意识和习惯,充分感知大家共同学习的快乐和意义。刚刚离开幼儿园的儿童,虽然已经有了一些集体生活学习的规则意识,但毕竟从没有像在校生一样上过课。学校的节奏也是极为陌生的。本课通过课堂、课下非常重要的一些环节帮助孩子建立良好的行为习惯,学会有利于更好地融入学习生活的方法和技能,认识到这些方法、规则的重要性,并且帮助孩子建立起应有的信心、亲近感和安全感。课程始终是以儿童生活为基础、通过多样的课堂活动把孩子课内所学与生活实际结合起来,让学生在活动游戏中得到感受、体验、探究和领悟,提升态度情感价值观。

xxxx线上主播合同
甲方:乙方:该协议为线上协议,签约时长为1年,签约后官方将保障协议双方的利益。一、双方达成线上签约协议后,甲方须履行以下职责:1. 对主播进行基本的艺能培训; 2. 为主播挖掘平台上的推广渠道; 3. 与主播充分沟通并制定基本的直播规划;当甲方未履行以上职责,乙方应与甲方充分沟通,并有权终止自己的直播。 二、乙方在签约期内,须履行以下义务: 1. 保证稳定的直播时间; 2. 保持密切的沟通; 3. 积极配合甲方的培训和推广活动; 4. 不得去非甲方合作平台的其他直播平台上进行视频表演;

森林防火动员大会领导讲话发言稿
当前,随着进入防火期,各县(市、区)要把森林防火工作列入重要议事日程,认真落实森林防火责任制。我们三农工作当中“三防一减”工作责任尤其重大,“三防”就是防汛、防火、防疫,“一减”就是减轻农民负担。我市的森林防火形势与全省一样,由于近年来市委、市政府的高度重视,加上各级林业部门的强力推进和四荒拍卖力度的不断加大,这几年我市新增造林面积将近103万亩,森林面积扩大也就增加了森林防火的任务量。特别是林州市、县西部、龙安区等地森林防火的难度、任务的艰巨程度比以往任何一年都加大,所以说必须加强领导,狠抓落实,做到领导到位、工作到位、各种保障到位。市森林防火指挥部市直各成员单位及各县(市、区)各成员单位,要认真按照森林防火指挥部的职责分工,切实做好各项工作。一旦发生火灾,各县(市、区)主要领导必须亲临一线,现场指挥扑火。

校长学校开学动员讲话发言稿多篇
本学期,在教育局领导下,为培养我们爱国主义精神,培养感恩意识,弘扬民族精神,充分反映我们热爱祖国,热爱家乡,奋发向上的精神风貌,我校将开展以爱祖国,爱家乡为活动主题的庆祝系列活动。活动的资料包括读书征文、手抄报、演讲比赛、书画比赛、主题班队会评比、歌咏比赛摄影展,我们还要开展以阳光下生长为主题的艺术节活动。同学们,新的学期开启新的期望,承载新的梦想,又为我们创造新成绩、新辉煌供给一个崭新的舞台。在那里我期望看到我们第七小学的学生能够自信的走向各种各样的舞台,去演绎你们的梦想,去实现你们的追求,你们要用自我的努力,去争取每一次的成功。

安全生产月活动表态发言讲话四分钟
项目自成立以来,在集团、公司的领导下始终坚持“安全第一,预防为主,综合治理的'”安全生产方针,深入开展以中建《施工现场安全防护标准化图册》和《XXX建筑工程施工现场扬尘污染防治实施细则》为指导,结合项目实际,绿色施工,打造安全文明标准化工地:施工现场安装可拆卸制式围墙,钢筋场、木工加工区、塔吊基础围护、材料堆场等采用1.8米格栅式工具化防护栏;施工区域分割、基坑周边防护、结构临边防护采用1.2米网片式工具化防护栏;现场主安全通道、建筑物出入口、施工电梯出入口及其它安全通道采用装配式安全防护棚。茶水间、休息室、吸烟室设置USB充电口及声控节能灯。现场施工对易产生扬尘的污染区采取封闭式作业,设置自动喷淋洒水系统、全自动洗车台,配备洒水车、雾炮机、PM10检测仪、现场视频监控系统等,对裸露土方采用了洒水、硬化、绿化、覆盖等有效抑尘措施。保护和改善施工环境和生态环境。

关于如何高效推动农业发展的调研报告
一、发展前景:质量优,效益高 全面建成小康社会,“短板”在“三农”。今年中央农村工作会议,明确要对标全面建成小康社会目标,提出保供给、保增收、保稳定的新要求。在新冠肺炎疫情冲击下,农业遭遇产销困难,如何推动农业转型升级,发展高效农业是重要方向。 高效农业以市场为导向,依靠科技支撑,以保障农产品供给、农民持续增收和农业可持续发展为目标,是经济、社会、生态综合效益最佳的农业。高效农业的核心要义,就是农业高质量、高效益,通过提高农业产业化、机械化、信息化水平,提高农业发展竞争力,是一二三产融合,种、养、加、销衔接,全产业链发展的现代农业新业态。发展高效农业,可以有效破解农业基础薄弱、生产规模偏小、供求矛盾突出、发展方式粗放等难题,是对传统农业的革命。

市“十四五”推进培育发展新动能调研报告
1.创新投入稳步增长。xx年全市研究与试验发展(R&D)经费为xx亿元,位居全省16位,R&D经费投入强度为xx。从全社会研发投入来看,xx年全社会研发投入xx亿元,较xx年增加xx亿元,增速为137%;xx年全社会研发投入xx亿元,投入较上年增加xx亿元,增长20%;xx年R&D经费投入增长到xx亿元,同比增加xx亿元,同比增长18.8%,较xx年增加了近xx亿元,较“十二五”末增长254.24%,年均增长52.44%。从全社会研发投入强度来看,xx年R&D经费投入强度上升幅度最大,由xx年的0.19%上升到0.42%,上升0.22个百分点;xx年R&D经费投入强度为0.46%,同比增长9.5%;xx年R&D经费投入强度为0.52%,同比增长13 %,较“十二五”末增长273%,全省的排名由16提升到12名(限于统计原因,R&D经费仅能统计20**年及以前数据)。全社会研发投入及强度均保持40%以上的增幅,充分说明市委、市政府及全社会越来越重视投入对科技创新的基础作用和支撑作用。

西北水利水电工程有限公司劳动合同
第十六条有下列情形之一,乙方可以随时通知甲方解除合同:1.甲方以暴力、威胁、监禁或者非法限制人身自由的手段强迫劳动的;2.甲方不能按照本合同规定支付劳动报酬或者提供劳动条件的。第十七条本合同期限届满,劳动合同即终止。双方当事人在本合同期满前30日内可以向对方表示续订意向,甲乙双方经协商同意,可以续订劳动合同。

