-

人教版高中历史必修3宋明理学说课稿3篇
陆王心学与程朱理学相比有何异同?生 不同点:在理的内涵上不同,程朱理学认为“理”是贯通于宇宙、人伦的客观存在,是一种普遍的规律准则;陆王心学认为心即理,是“良知”,认为人心便是世界万物的本原。方法上也有不同:前者向外追究,“格物致知”;后者向内探求,“发明本心”以求理,克服私欲、回复良知。生 相同点:都提出了一个宇宙、社会、人生遵循的“理”。师 对。程朱理学是客观唯心主义,阳明心学是主观唯心主义。这两者的分歧是理学范围内的分歧,其基本思想是一致的。师 宋明理学与汉唐以前的儒学比较,最大的特点在于批判地吸收了佛教哲学的思辨结构和道教的宇宙生成论,将儒家的伦理学说概括升华为哲学基本问题。其实质是把佛、道“养性”“修身”引向儒家的“齐家”“治国”“平天下”,对儒家的纲常道德给予哲学论证,使之神圣化、绝对化、普遍化,以便深入人心,做到人人遵而行之。

新人教版高中英语必修3Unit 4 Space Exploration-Discovering Useful Structures导学案
【点津】 1.不定式的复合结构作目的状语 ,当不定式或不定式短语有自己的执行者时,要用不定式的复合结构?即在不定式或不定式短语之前加 for +名词或宾格代词?作状语。He opened the door for the children to come in. 他开门让孩子们进来。目的状语从句与不定式的转换 英语中的目的状语从句,还可以变为不定式或不定式短语作状语,从而使句子在结构上得以简化。可分为两种情况: 1?当目的状语从句中的主语与主句中的主语相同时,可以直接简化为不定式或不定式短语作状语。We'll start early in order that/so that we may arrive in time. →We'll start early in order to/so as to arrive in time. 2?当目的状语从句中的主语与主句中的主语不相同时,要用动词不定式的复合结构作状语。I came early in order that you might read my report before the meeting. →I came early in order for you to read my report before the meeting.

学生会学习宣传部工作制度
一、工作任务:负责学校的校刊及墙板报,每月出刊一次 二、工作态度:认真、负责、积极、行为端正、为人正直、相互团结、和谐相处 三、工作纪律要求: 1、工作方面 (1)在出刊时成员应注重效率和质量 (2)不做有损学生会及本部名誉的事 (3)工作中应积极配合部长或副部长的工作安排

国旗下讲话:《讲究方法,学会学习》
老师们、同学们:早上好,今天国旗下讲话的题目是《讲究方法,学会学习》。说到学习方法,每个人的看法不尽相同,就好像同一棵树上不可能长出两片完全相同的叶子一样,但是我想以下三点还是被大家所认同的。一、兼收并蓄。同学们,你们到过海边看过大海吗?当你站在海边望着无边的大海,领略那惊涛拍岸、卷起千层浪的壮观景色,你是否感到震撼?为什么大海会有如此磅礴的气势?因为大海以它博大的胸怀,容纳了无数的河川,这就是兼收并蓄。今天面对着科学日新月异的迅猛发展,我们也要有这样的态度,从多种渠道获取知识。如在校认真学习,互相取长补短,有时间在书店或图书馆看一看,也可以从互联网上获取有用的信息来丰富自己。再拿语文学科的学习来说吧,我们就要进行广泛深入的阅读,内容涵盖古今中外、自然社会。凡是人类心灵和智慧的结晶均可兼收并蓄。对于一些经典作品,应当精读,细读,甚至背诵。“读书破万卷,下笔如有神”,虽是古人学习写作的经验之谈,但也道出了广泛阅读、兼收并蓄的重要性。

高二学生国旗下讲话:在思想下学习
尊敬的老师们、亲爱的同学们:大家早上好!前些天,诺贝尔奖得主陆陆续续揭晓,这些与我们朝夕相处的学科,在十月份聚焦了人们的目光,也让人看到了这些基础学科的力量。说这些,肯定会有人对此不屑,我们每天打交道的语文,不过是背一些东西,写一些废话,学几篇课文,我们每天打交道的理化生,不过就是做一些题,背一些结论,考几次试。这就是我们对真正的学习所持有的态度和方式吗?我们与这些基础学科相伴了多少年,认识仅停留于表象吗?这里可以与大家分享几个例子。1957年诺贝尔奖得主杨振宁曾说,他在西南联大时老师辛勤讲授的基础知识给了他扎实的功底,这些在后来依然有用。留学时导师要来时不时地提出一些新观点也给他留下了深刻的印象。

数学教师工作计划
一、加强教育教学理论学习,提高个人的理论素养 1. 认真学习教学大纲和有关数学课程等材料。 2. 加大对自己和学生的自我分析和解剖。 二、按数学课程标准,进行教学研究,提高课堂教学效益

实习师范教师简历
XXX软件有限公司 / 教研组201x.09 - 202x.06实习老师1. 协助班主任管理班级,组织班级活动(组织班会及课外活动);2. 出现问题时,及时与学生任课老师,班主任及家长沟通解决问题3. 担任学生班主任,负责五年级xx余名学生的生活与学习4. 担任「公司/组织」实验班班实习班主任,在实习中深入了解高中生的学习情况和生活状态;5. 担任实习班主任具有良好的组织能力和领导能力,组织了班级的秋冬季运动会入场等相关活动。6. 作为艺考生的班主任在「日期/时间」工作中与他们一起学习并检查他们播音发声以及xx背诵在「日期/时间」会教他们播音的基础发声以及练习有着比较丰富的工作经验

部编版语文八年级下册《庆祝奥林匹克运动复兴25周年》说课稿
一.说教材 1.教材所处的地位《庆祝奥林匹克运动复兴25周年》是人教版部编初中语文教材八年级下册第四单元“思想光芒”中的一篇经典演讲词。它是同学们接触过《 最后一次讲演》《应有格物致知精神》《我一生中的重要抉择》,初步了解、掌握关于演讲的一些技巧之后,再次让学生倾听那些穿越时空的声音,感受演讲精品的魅力,并总结、借鉴典范演讲的经验,在历练中提高演说才能。因为在现代社会中,良好的口语交际能力是公民的重要素养之一,它不但显示着一个人的语言水平,更体现着一个人的自信、智慧、教养与风度。2.教材分析 《庆祝奥林匹克运动复兴25周年》是顾拜旦于1919年4月在瑞士洛桑庆祝奥林匹克运动恢复25周年纪念会上的演说,是关于奥林匹克运动的重要文献。顾拜旦用诗歌般的语言阐述了奥林匹克精神的内涵与价值;以饱含喜悦的神情引领听众去联想奥林匹克精神无限美好的前景。这篇演说词和他的诗歌《体育颂》一起成为世界文化史和体育史上不朽的篇章。

用空间向量研究直线、平面的位置关系(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、空间中点、直线和平面的向量表示1.点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量(OP) ?来表示.我们把向量(OP) ?称为点P的位置向量.如图.2.空间直线的向量表示式如图①,a是直线l的方向向量,在直线l上取(AB) ?=a,设P是直线l上的任意一点,则点P在直线l上的充要条件是存在实数t,使得(AP) ?=ta,即(AP) ?=t(AB) ?.如图②,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使(OP) ?=(OA) ?+ta, ①或(OP) ?=(OA) ?+t(AB) ?. ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.1.下列说法中正确的是( )A.直线的方向向量是唯一的B.与一个平面的法向量共线的非零向量都是该平面的法向量C.直线的方向向量有两个D.平面的法向量是唯一的答案:B 解析:由平面法向量的定义可知,B项正确.

空间向量及其运算的坐标表示教学设计人教A版高中数学选择性必修第一册
一、情境导学我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.二、探究新知一、空间直角坐标系与坐标表示1.空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.

抛物线及其标准方程教学设计人教A版高中数学选择性必修第一册
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》,本节课主要学习抛物线及其标准方程在经历了椭圆和双曲线的学习后再学习抛物线,是在学生原有认知的基础上从几何与代数两 个角度去认识抛物线.教材在抛物线的定义这个内容的安排上是:先从直观上认识抛物线,再从画法中提炼出抛物线的几何特征,由此抽象概括出抛物线的定义,最后是抛物线定义的简单应用.这样的安排不仅体现出《课程标准》中要求通过丰富的实例展开教学的理念,而且符合学生从具体到抽象的认知规律,有利于学生对概念的学习和理解.坐标法的教学贯穿了整个“圆锥曲线方程”一章,是学生应重点掌握的基本数学方法 运动变化和对立统一的思想观点在这节知识中得到了突出体现,我们必须充分利用好这部分教材进行教学

双曲线及其标准方程教学设计人教A版高中数学选择性必修第一册
∵在△EFP中,|EF|=2c,EF上的高为点P的纵坐标,∴S△EFP=4/3c2=12,∴c=3,即P点坐标为(5,4).由两点间的距离公式|PE|=√("(" 5+3")" ^2+4^2 )=4√5,|PF|=√("(" 5"-" 3")" ^2+4^2 )=2√5,∴a=√5.又b2=c2-a2=4,故所求双曲线的方程为x^2/5-y^2/4=1.5.求适合下列条件的双曲线的标准方程.(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;(2)以椭圆x^2/8+y^2/5=1长轴的端点为焦点,且经过点(3,√10);(3)a=b,经过点(3,-1).解:(1)由双曲线的定义知,2a=8,所以a=4,又知焦点在x轴上,且c=5,所以b2=c2-a2=25-16=9,所以双曲线的标准方程为x^2/16-y^2/9=1.(2)由题意得,双曲线的焦点在x轴上,且c=2√2.设双曲线的标准方程为x^2/a^2 -y^2/b^2 =1(a>0,b>0),则有a2+b2=c2=8,9/a^2 -10/b^2 =1,解得a2=3,b2=5.故所求双曲线的标准方程为x^2/3-y^2/5=1.(3)当焦点在x轴上时,可设双曲线方程为x2-y2=a2,将点(3,-1)代入,得32-(-1)2=a2,所以a2=b2=8.因此,所求的双曲线的标准方程为x^2/8-y^2/8=1.当焦点在y轴上时,可设双曲线方程为y2-x2=a2,将点(3,-1)代入,得(-1)2-32=a2,a2=-8,不可能,所以焦点不可能在y轴上.综上,所求双曲线的标准方程为x^2/8-y^2/8=1.

用空间向量研究距离、夹角问题(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、点到直线的距离、两条平行直线之间的距离1.点到直线的距离已知直线l的单位方向向量为μ,A是直线l上的定点,P是直线l外一点.设(AP) ?=a,则向量(AP) ?在直线l上的投影向量(AQ) ?=(a·μ)μ.点P到直线l的距离为PQ=√(a^2 "-(" a"·" μ")" ^2 ).2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.点睛:点到直线的距离,即点到直线的垂线段的长度,由于直线与直线外一点确定一个平面,所以空间点到直线的距离问题可转化为空间某一个平面内点到直线的距离问题.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 . 答案: √174/6解析:如图,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),E(0,2,1),F(1,0,2),(EF) ?=(1,-2,1),

用空间向量研究直线、平面的位置关系(2)教学设计人教A版高中数学选择性必修第一册
跟踪训练1在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC;(2)BD1⊥EB1.(2)∵(BD_1 ) ?=(-1,-1,1),(EB_1 ) ?=(1/2 "," 1/2 "," 1),∴(BD_1 ) ?·(EB_1 ) ?=(-1)×1/2+(-1)×1/2+1×1=0,∴(BD_1 ) ?⊥(EB_1 ) ?,∴BD1⊥EB1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E(1/2 "," 1/2 "," 0),B1(1,1,1).(1)∵(BD_1 ) ?=(-1,-1,1),(AC) ?=(-1,1,0),∴(BD_1 ) ?·(AC) ?=(-1)×(-1)+(-1)×1+1×0=0.∴(BD_1 ) ?⊥(AC) ?,∴BD1⊥AC.例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.思路分析一种思路是不建系,利用基向量法证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直,从而根据线面垂直的判定定理证得结论;另一种思路是建立空间直角坐标系,通过坐标运算证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直;还可以在建系的前提下,求得平面EFB1的法向量,然后说明(D_1 M) ?与法向量共线,从而证得结论.证明:(方法1)因为E,F,M分别为棱AB,BC,B1B的中点,所以(D_1 M) ?=(D_1 B_1 ) ?+(B_1 M) ?=(DA) ?+(DC) ?+1/2 (B_1 B) ?,而(B_1 E) ?=(B_1 B) ?+(BE) ?=(B_1 B) ?-1/2 (DC) ?,于是(D_1 M) ?·(B_1 E) ?=((DA) ?+(DC) ?+1/2 (B_1 B) ?)·((B_1 B) ?-1/2 (DC) ?)=0-0+0-1/2+1/2-1/4×0=0,因此(D_1 M) ?⊥(B_1 E) ?.同理(D_1 M) ?⊥(B_1 F) ?,又因为(B_1 E) ?,(B_1 F) ?不共线,因此D1M⊥平面EFB1.

小学美术人教版二年级上册《第9课蜻蜓飞飞》教案说课稿
1、引导学生观察蜻蜓,抓住蜻蜓的特点进行绘画创作。2、充分发挥学生的想象和创造能力。课前准备:教具:课件、模具、图片、有关作品。学具:作业纸、画笔。教学过程一、导入课题1.教师出示一张纸,变成折纸蜻蜓激起学生兴趣。2.出示课题:蜻蜓飞飞二、新授课1、交流课前收集的资料。请学生谈谈收集的关于蜻蜓的知识,教师补充介绍。2、学生仔细观察蜻蜓模具,结合课件图片小组内交流讨论:蜻蜓是由哪些部分组成的,各有怎样的特点?
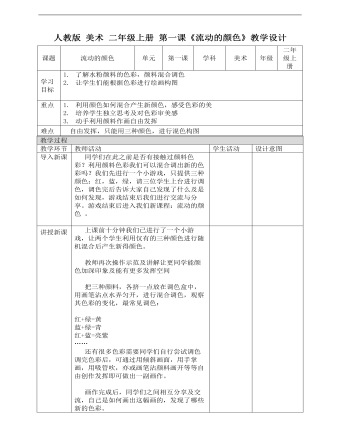
小学美术人教版二年级上册《第1课流动的颜色》教案说课稿
同学们在此之前是否有接触过颜料色彩?利用颜料色彩我们可以混合调出新的色彩吗?我们先进行一个小游戏,只提供三种颜色:红,蓝,绿,请三位学生上台进行调色,调色完后告诉大家自己发现了什么及是如何发现,游戏结束后我们进行交流与分享。游戏结束后进入我们新课程:流动的颜色 。

小学美术人教版一年级下册《第6课摸一摸画一画》教案说课稿
一、对比图片明确目标两幅表现“热”的图片进行对比,先给大家看两幅非常有意思的画。第一幅:画的什么内容?随着环境的破坏,地球的逐渐升温,圣诞老人也脱下了棉服换上了夏装。圣诞老人为什么不再愿意穿棉衣了呢?因为圣诞老人感觉到天气太热了。第二幅:小作者说“我画的也是热的感觉。”同样都是表现“热”的感觉,它与第一幅有什么不同?它画具体的形象了吗?象这种不具象的画就是抽象画,这节课咱们就来研究怎样用抽象画的形式来表现感觉。揭题:摸一摸画一画

小学美术人教版一年级上册《第20课美丽的植物和动物》教案说课稿
2、懂得要爱护动植物,对破坏植物、残杀动物的行为表示气愤,在日常生活中能自觉做到爱护动植物,不做破坏动植物生态环境的事,积极参加保护动植物的公益活动。活动重点:感受动植物的生命现象,懂得爱护动植物。

小学美术人教版一年级上册《第1课认识美术工具》教案说课稿
1、引导学生认识各种美术工具和材料。2、引导学生用不同的美术工具和材料,大胆、自由地表达自己的各种想法。3、引导学生在认识美术工具和材料的过程中对美术课产生兴趣。教学重点:了解不同的用具和材料能制作不同的绘画作品。教学难点:学生自己能用工具和材料自由的表达自己的情感。教学方法:游戏相结合、观察比较法、谈话法
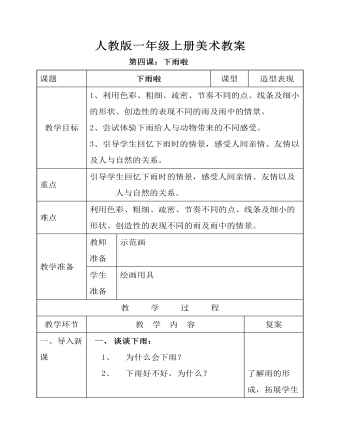
小学美术人教版一年级上册《第4课下雨啦》教案说课稿
1、利用色彩、粗细、疏密、节奏不同的点、线条及细小的形状、创造性的表现不同的雨及雨中的情景。2、尝试体验下雨给人与动物带来的不同感受。3、引导学生回忆下雨时的情景,感受人间亲情、友情以及人与自然的关系。

