-
空间向量及其运算的坐标表示教学设计人教A版高中数学选择性必修第一册
一、情境导学我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.二、探究新知一、空间直角坐标系与坐标表示1.空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.
抛物线及其标准方程教学设计人教A版高中数学选择性必修第一册
本节课选自《2019人教A版高中数学选择性必修第一册》第二章《直线和圆的方程》，本节课主要学习抛物线及其标准方程在经历了椭圆和双曲线的学习后再学习抛物线，是在学生原有认知的基础上从几何与代数两 个角度去认识抛物线.教材在抛物线的定义这个内容的安排上是：先从直观上认识抛物线，再从画法中提炼出抛物线的几何特征，由此抽象概括出抛物线的定义，最后是抛物线定义的简单应用.这样的安排不仅体现出《课程标准》中要求通过丰富的实例展开教学的理念，而且符合学生从具体到抽象的认知规律，有利于学生对概念的学习和理解.坐标法的教学贯穿了整个“圆锥曲线方程”一章，是学生应重点掌握的基本数学方法 运动变化和对立统一的思想观点在这节知识中得到了突出体现，我们必须充分利用好这部分教材进行教学
双曲线的简单几何性质（2）教学设计人教A版高中数学选择性必修第一册
二、典例解析例4．如图，双曲线型冷却塔的外形，是双曲线的一部分，已知塔的总高度为137.5m，塔顶直径为90m，塔的最小直径(喉部直径)为60m，喉部标高112.5m，试建立适当的坐标系，求出此双曲线的标准方程（精确到1m）解:设双曲线的标准方程为 ，如图所示：为喉部直径，故 ，故双曲线方程为 .而 的横坐标为塔顶直径的一半即 ，其纵坐标为塔的总高度与喉部标高的差即 ，故 ，故 ，所以 ，故双曲线方程为 .例5．已知点 到定点 的距离和它到定直线l: 的距离的比是 ，则点 的轨迹方程为?解：设点 ，由题知, ，即 .整理得： .请你将例5与椭圆一节中的例6比较，你有什么发现？例6、 过双曲线 的右焦点F2,倾斜角为30度的直线交双曲线于A,B两点,求|AB|.分析:求弦长问题有两种方法:法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.解：由双曲线的方程得，两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°，且直线经过右焦点F2，所以，直线AB的方程为
双曲线及其标准方程教学设计人教A版高中数学选择性必修第一册
∵在△EFP中,|EF|=2c,EF上的高为点P的纵坐标,∴S△EFP=4/3c2=12,∴c=3,即P点坐标为(5,4).由两点间的距离公式|PE|=√("(" 5+3")" ^2+4^2 )=4√5,|PF|=√("(" 5"-" 3")" ^2+4^2 )=2√5,∴a=√5.又b2=c2-a2=4,故所求双曲线的方程为x^2/5-y^2/4=1.5.求适合下列条件的双曲线的标准方程.(1)两个焦点的坐标分别是(-5,0),(5,0),双曲线上的点与两焦点的距离之差的绝对值等于8;(2)以椭圆x^2/8+y^2/5=1长轴的端点为焦点,且经过点(3,√10);(3)a=b,经过点(3,-1).解:(1)由双曲线的定义知,2a=8,所以a=4,又知焦点在x轴上,且c=5,所以b2=c2-a2=25-16=9,所以双曲线的标准方程为x^2/16-y^2/9=1.(2)由题意得,双曲线的焦点在x轴上,且c=2√2.设双曲线的标准方程为x^2/a^2 -y^2/b^2 =1(a>0,b>0),则有a2+b2=c2=8,9/a^2 -10/b^2 =1,解得a2=3,b2=5.故所求双曲线的标准方程为x^2/3-y^2/5=1.(3)当焦点在x轴上时,可设双曲线方程为x2-y2=a2,将点(3,-1)代入,得32-(-1)2=a2,所以a2=b2=8.因此,所求的双曲线的标准方程为x^2/8-y^2/8=1.当焦点在y轴上时,可设双曲线方程为y2-x2=a2,将点(3,-1)代入,得(-1)2-32=a2,a2=-8,不可能,所以焦点不可能在y轴上.综上,所求双曲线的标准方程为x^2/8-y^2/8=1.
《春之声》教案
启发导入、初步感悟。播放音乐《春之声》片段A师：听的过程中，可以随音乐轻轻东移动，用身体表示出你的感受。（随音乐做简单律动）听完后告诉老师：在这段音乐中同学们感受到了什么？想做什么？有没有想跳舞的冲动？情绪怎样？能不能听出是几拍子的？（活泼、欢快、节奏感强，是三拍子的）一般舞曲都是三拍子的。（三拍子引出圆舞曲。）介绍约翰?施特劳斯被称为“圆舞曲之王”，他一生做了五百多首乐曲。（讲解一下为什么是小约翰?施特劳斯，因为小约翰?施特劳斯的父亲是叫约翰?施特劳斯，为了加以区别所以加个小。他父亲也是个音乐家，著名的《拉德斯基进行曲》就是他父亲创作的。而小约翰?施特劳斯主要创作的是圆舞曲。下面就带大家来欣赏一下由奥地利音乐家小约翰?施特劳斯创作的《春之声》。）
《春之声》教案
一、找春天，听春天的声音 1、导语： 师：课前我请大家在校园中找春天，你找到了吗？请你说一说，春天在哪里？生：… … 师：你们说的春天都很美。大家还记得《春晓》这首诗吗？让我们带着各自对春天不同的感受来朗诵这首诗吧！ 春眠不觉晓， 处处闻啼鸟。 夜来风雨声， 花落知多少？ 师：在这首诗里你听到了春天里的哪些声音？ 生：鸟叫… … 师：好！那么我们现在来听一听奥地利著名音乐家约翰·施特劳斯创作的《春之声》，请你在这首乐曲中找一找春天的声音。 2、初听全曲 （1）以小组为单位将他们听到的春天的声音写在小黑板上。 （2）各自说一说自己听完音乐后想象到的春天的景象。
《春之声》教案
教学过程：一、创设情境设计意图：通过复习歌曲，使学生进入春天的情境，引出本课教学。1、有感情地演唱歌曲《春天举行音乐会》，表达春天到来时人们美好的心情。2、表演唱歌曲《嘀哩嘀哩》，体会小朋友在寻找春天时神秘、喜悦、自豪的心情。3、感受回旋式曲式。二、方法（1）教师弹奏包括引子和尾奏在内的八个音乐主题，学生根据事先准备好的八种色块，选择分别代表的主题，并标注顺序。然后，重点视唱A和B两个音乐主题。进行对比。（2）再次聆听全曲，看着课件摆色块。如有重复，用备用的色块。（要求学生准备三份色块）（3）简介回旋曲式和《春之声》。三、赞美春天师：春天是美丽的、动人的、充满生机的，它就像一幅绚丽的画、一首动听的歌、一段醉人的舞，现在就让我们来创编我们心中的春天。
大班语言教案：《风中之叶》
2、学习运用各种感官进行有趣的描述。3、在游戏中发挥想象，创编儿歌《落叶飘》。二、 活动准备：1、环境布置：活动室内布置有小河、草地、马路。2、材料准备：人手一张不同形状的树叶。3、事先教唱歌曲《小树叶》。三、 活动过程：1、游戏：“捡落叶”（1） 师：今天老师带来了好多树妈妈的小宝贝，你们猜猜是谁？幼：是小树叶。（2） 师：一阵风吹过来，小树叶吹走了，赶紧去捡起来吧。幼儿每人捡一片自己喜欢的落叶。（3） 请幼儿描述一下自己的落叶长得什么样？并用形体动作表现出叶子的造型。（长长的、宽宽的、尖尖的、圆圆的、破一个洞的------）
人教版新课标小学数学一年级下册20以内的退位减法教案2篇
一、揭题：小朋友们，今天我们一起来做练习。二、练习：1、第8题：这是一道计算题。（1）明确要求：看谁算得又对又快。（2）学生独立完成。（3）订正答案。（4）有错的学生，说一说计算顺序是怎样的，每一步的计算结果是多少？2、第9题：这是一道用数学的题。（1）看图，同位两个互相说说图意，并提出数学问题。（2）根据问题列算式解答。（3）订正答案。3、第10题：比一比。（1）明确要求，看谁先夺得红旗。（2）各小组派代表参加比赛。（3）对算得又对又快的学生提出表扬，并奖励给一个小标志。（4）再加入几组比赛题，尽量让学生多参与。4、第11题：这是一道用数学的题。（1）看图，说图意，提出数学问题。（2）列算式解答，指名板演订正。（3）说一说为什么用加法计算？5、思考题：小组讨论完成。一共12人，每两人之间插入一个女生，一共能插入11人。
人教部编版语文九年级上册孤独之旅教案
（3）对未来前途的恐惧：漫漫放鸭路，何处是尽头？对前途的迷茫和惶恐。学会深度解读题目，能帮助学生更好地理解人物形象、情感脉络以及文章主旨。引导学生结合生活体验加深对“孤独”的理解，对于学生的思维深度开发有好处，同时对于作文诗意化拟题也大有裨益。三、拓展，走出孤独有些孤独，其实是我们成长过程中的一些无法回避的元素。我们要成长，就不能不与这些孤独结伴而行。——曹文轩1.思考问题从哪些地方可以看出杜小康走出孤独，走向成熟了呢？旁批：暖色的结尾，充满希望。课件出示：他惊喜地跑过去捡起，然后朝窝棚大叫：“蛋！爸！鸭蛋！鸭下蛋了！”杜雍和从儿子手中接过还有点儿温热的蛋，嘴里不住地说：“下蛋了，下蛋了……”预设：风雨过后是彩虹，孤独痛苦是成长的催化剂。暗示主人公走向成熟。这叫喊声里满是成长的自豪和骄傲。
人教部编版语文九年级下册无言之美教案
如何理解文中对于言与意关系的分析？文章分析了言和意的关系，认为言是用以表达情感意绪的工具，但意“决不是完全可以”用言来传达的。因为意是丰富的、无限的、缥缈易逝的，具有混整的特性；而一旦用言语表现出来，意思就固定了、单一了，如果再考虑交流中信息的损耗、接受者理解的不同等因素，用言来表现的意就会出现偏差，而失去其丰富性。这里道出了人类语言先天的局限性。自从产生语言，人类逐渐习惯于以语言来思维，以固定的语义系统来指称和描述外在世界，但世界是丰富的、具体的，语言却是概括的、抽象的，再完备的语义系统，都无法完全准确地指称和描摹每一个个体事物。 黑格尔甚至断言:“语言本质上只表达普遍的东西，但人们所想的却是特殊的东西，因此不能用语言表达人们所想的东西。”因而，作者说，以言语来表达丰富的“意”，“好像用断续的虚线画实物，只能得其近似”。当然，如果通过词语、概念的辨析，使语言表述精确化、严密化，或者采用修辞或文学的手段，拓展语言的表现力和表现空间，就可以尽可能地使“言” 来表达丰富的“意”。
人教A版高中数学必修一二次函数与一元二次方程、不等式教学设计（2）
三个“二次”即一元二次函数、一元二次方程、一元二次不等式是高中数学的重要内容，具有丰富的内涵和密切的联系，同时也是研究包含二次曲线在内的许多内容的工具 高考试题中近一半的试题与这三个“二次”问题有关 本节主要是帮助考生理解三者之间的区别及联系，掌握函数、方程及不等式的思想和方法。课程目标1. 通过探索，使学生理解二次函数与一元二次方程，一元二次不等式之间的联系。2. 使学生能够运用二次函数及其图像，性质解决实际问题． 3. 渗透数形结合思想，进一步培养学生综合解题能力。数学学科素养1.数学抽象：一元二次函数与一元二次方程，一元二次不等式之间的联系；2.逻辑推理：一元二次不等式恒成立问题；3.数学运算：解一元二次不等式；4.数据分析：一元二次不等式解决实际问题；5.数学建模：运用数形结合的思想，逐步渗透一元二次函数与一元二次方程，一元二次不等式之间的联系。
人教A版高中数学必修一两角和与差的正弦、余弦和正切公式教学设计（2）
本节内容是三角恒等变形的基础，是正弦线、余弦线和诱导公式等知识的延伸，同时，它又是两角和、差、倍、半角等公式的“源头”。两角和与差的正弦、余弦、正切是本章的重要内容，对于三角变换、三角恒等式的证明和三角函数式的化简、求值等三角问题的解决有着重要的支撑作用。 课程目标1、能够推导出两角和与差的正弦、余弦、正切公式并能应用; 2、掌握二倍角公式及变形公式，能灵活运用二倍角公式解决有关的化简、求值、证明问题．数学学科素养1.数学抽象：两角和与差的正弦、余弦和正切公式； 2.逻辑推理： 运用公式解决基本三角函数式的化简、证明等问题；3.数学运算：运用公式解决基本三角函数式求值问题.4.数学建模：学生体会到一般与特殊，换元等数学思想在三角恒等变换中的作用。.
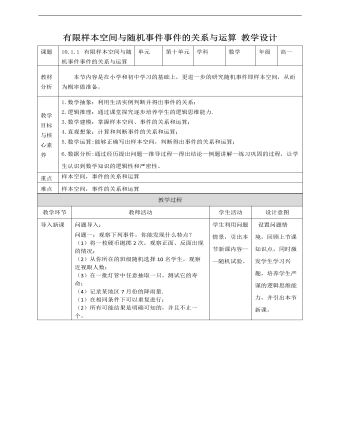
人教A版高中数学必修二有限样本空间与随机事件事件的关系和运算教学设计
新知讲授（一）——随机试验 我们把对随机现象的实现和对它的观察称为随机试验，简称试验，常用字母E表示。我们通常研究以下特点的随机试验：（1）试验可以在相同条件下重复进行；（2）试验的所有可能结果是明确可知的，并且不止一个；（3）每次试验总是恰好出现这些可能结果中的一个，但事先不确定出现哪个结果。新知讲授（二）——样本空间思考一：体育彩票摇奖时，将10个质地和大小完全相同、分别标号0，1，2，...，9的球放入摇奖器中，经过充分搅拌后摇出一个球，观察这个球的号码。这个随机试验共有多少个可能结果？如何表示这些结果？根据球的号码，共有10种可能结果。如果用m表示“摇出的球的号码为m”这一结果，那么所有可能结果可用集合表示{0，1，2，3，4，5，6，7，8，9}.我们把随机试验E的每个可能的基本结果称为样本点，全体样本点的集合称为试验E的样本空间。
《蓓蕾之歌》教案
一、导入新课从蓓蕾长成为鲜花，从幼苗成长为大树，幼苗成长为大树，离不开园丁的辛勤劳动。老师就像园丁，精心培育着我们，使我们健康成长。让我们倾听一首唱给老师的歌！二、教学过程（一）欣赏《蓓蕾之歌》1、初听歌曲《蓓蕾之歌》师：这首歌曲带给你什么样的感受？生：（讨论）师：这首歌曲是深情的、抒情的，是李岚清副总理在1999年秋第三届全国教育会议期间举办的艺术歌曲音乐会而创作，赞美了老师无私奉献之情。2、复听歌曲《蓓蕾之歌》师：是什么原因让歌曲拥有这种情绪呢？让我们再次聆听歌曲，从速度、节拍、节奏这些音乐要素方面来分析一下。
《花之圆舞曲》教案
教学目的：感受不同情趣的音乐，提高学生欣赏名曲的能力。教学内容：欣赏《花之圆舞曲》。教具：录音机。教学过程：一、组织教学。二、听音练习。A、1、2、3、4、5、6、7、5、2、B、3、1、4、2、5、7、1、
《音乐之声》教案
教学过程：1、在《音乐之声》的歌声中走进教室，初步体会歌曲中对于音乐的赞美之情。2、教师简介《音乐之声》这部电影的内容，播放课件，配合视频和音乐让学生了解电影的时代背景和故事情节，图像、声音、内容合为一体，给学生最直观的感受，为下面欣赏歌曲做好铺垫。3、介绍并欣赏主题曲《音乐之声》创作背景及相关内容，让学生进一步了解歌曲的内容和情感风格。4、播放《音乐之声》在影片中的片段，欣赏原汁原味的电影歌曲，体会歌曲情感，分析歌曲内容，感受四四拍的节奏，让学生说出欣赏感受，并再次欣赏《音乐之声》，鼓励学生跟着哼唱。提示学生注意演唱形式的变换。5、思考歌曲的演唱形式，介绍独唱、齐唱，比较合唱与重唱的异同，并提醒学生注意在演唱二声部时第一要注意唱准自己声部的旋律，二要相互配合，和谐统一。6、欣赏影片中的其他插曲《Do Re Mi》和《孤独的牧羊人》，分别播放从电影中剪辑下来的视频，体会不同的音乐风格与乐趣。说出两首歌曲带给我们的感受（《哆来咪》欢乐有趣，《孤独的牧羊人》诙谐幽默）。引导学生思考音乐在电影中的重要作用：烘托情感，渲染气氛，让感情发挥的淋漓尽致，让电影得到更完美的诠释。7、小结及作业：适当的时间自己欣赏《音乐之声》这部影片，完整体会影片和歌曲的魅力。
《音乐之声》教案
教学过程：一、创设情境 初步体验1、组织教学，师生问好！2、引入课题。师：同学们你们知道奥斯卡金像奖吗？3、师：有一部曾获得过奥斯卡7个奖项的音乐电影《音乐之声》，这部电影主要讲的是：有一个叫玛丽亚的修女，来到一位海军上校家当家庭教师，上校的七个孩子很调皮，她用爱心与音乐和七个失去母亲的孩子成为了好朋友，并教会了孩子许多歌曲，使他们得到慈母般的温暖。（播放多媒体《音乐之声主题曲》）4、导言。师：我们今天就来学习唱唱这首歌。让大家跟着老师一起去欣赏歌曲中所体现的对于音乐的热爱之情。二、探究新知，感受体验1、师：请同学们认真地听，说出这首歌的演唱情绪！（优美、缓慢）这就是我们今天要学习的歌曲《音乐之声》，这首歌是《音乐之声》中的主题曲，是一首美国歌曲，歌曲为4/4拍，C大调。（板书）2、模唱歌曲，体会音乐要素（层次变化）师：下面让我们随着音乐，轻声地填唱歌词，感受歌曲的旋律。（播放《音乐之声》范唱，学生轻声跟唱）3、师：下面请同学们跟着老师的琴声一起来学唱吧！（教师指导学生跟琴学唱）师：在这首歌曲中出现了变化音，谁能找到它？现在让我们来唱一唱。（重点指导有变化音的乐句，指导学生有感情的演唱歌曲。）
《大漠之夜》教案
教学过程：一、导入二、学习歌曲1、老师范唱，思考：大漠之夜美丽在什么地方？2、老师简介歌曲。3、学生边划拍边学唱歌谱。4、跟老师的伴奏哼唱歌谱。5、按节奏读歌词。6、跟伴奏演唱歌曲。7、完整演唱。三、就地取材自制打击乐器，创编节奏为歌曲伴奏。四、小结： 1、表扬以最简单的废品自制有效果的打击乐器参与表演的同学。2、分组选择音乐段落，设计舞蹈动作。3、大漠之夜真美。回家收集以花为题材的歌曲或乐曲，并进行学唱。4、布置作业：将收集到的以大漠为题材的资料，在下节课我们开一次班级音乐会。
《大漠之夜》教案
教学过程：师：今天我们要到音乐中的大漠里去畅游一番，让我们在动听的歌声中开始旅行吧！（播放《大漠之夜》。）师：同学们，你们仔细听一听，这歌曲中唱的是什么大漠？生：……师：你去过大漠吗？你认为大漠是怎样啊？生：……师：如果你没去过大漠，也没关系，老师这儿有照片，现在我们来看看大漠的照片。（播放大漠照片。）师：现在我们再来听一遍《大漠之夜》，你觉得作者想要表达的是什么思想感情？（再次播放《大漠之夜》。）生：……课后小结：希望同学们涉猎更多的艺术形式，开阔艺术视野，感受各种艺术表现形式带来的美的享受。
