-

XX-XX第二学期第六周国旗下讲话稿:珍惜粮食,做勤勉节俭的xx学子
尊敬的老师、领导,亲爱的同学们:大家早上好!今天我发言的题目是“珍惜粮食,做勤勉节俭的xx学子”。关于这个题目,我的发言有三点。第一,珍惜粮食,从我做起。“谁知盘中餐,粒粒皆辛苦”告诉了我们粮食来之不易的道理。学校领导很早就倡导全校师生开展“光盘行动”:盘里不剩菜,碗里不剩米。无论对于老师还是学生,这个标准都不能打任何折扣。可是现在,我们仍然可以看到有同学浪费食物的现象,吃不完的米饭随意倒掉,而且很“大方”、不犹豫。试想,我们学校近300名师生就餐,每人每顿少浪费一粒米,这数额积累下来,至少可以让一个饱受饥饿之苦的人解决温饱问题,这样下来,又可以节约资源求得学校更好的发展,何乐而不为呢?都说温饱不忘饥寒,增产不忘节约。我们处在衣食无忧的好时代,学校也处在稳步发展的关键时期,我们要从自身做起,珍惜粮食,杜绝浪费。

2023在“招商引资突破年”“重大项目推进年”誓师大会上的讲话稿
同志们:把今天的“招商引资突破年”和“重大项目推进年”会议名称确定为誓师大会,意味着战前动员,昭示着县委、县政府举全县之力抓招商、抓项目的决心不改变、信心不动摇、力度不减弱,主要目的在于部署任务、传导压力、压实责任,以“开局就是决战、起步就是冲刺”的紧迫感,点燃干事的激情、激发工作的斗志,动员全县上下撸起袖子加油干、全力以赴向前冲,吹响招商引资工作冲锋号,奏响重大项目建设进行曲,奋力谱写*转型跨越壮美乐章。这个会议,既是落实县委十三届三次全会明确的深入开展“四个年”活动中两个“首战年”任务,也是贯彻年初的市委经济工作会议精神。为了开好这个会议,我们从*年第四季度工作汇报会后就开始筹备,重点在于制定这“两个年”的活动方案,今天一起随会议汇编印发给大家,共涉及10余个政策措施文件。“两个年”的活动方案,县级分管领导和责任部门做了大量的调查研究工作,也借鉴了外地一些成功做法和经验,春节前我和县长就专题听过一次汇报,春节后又分别经过县政府常务会和县委常委会研究。应该说,出台的政策科学规范,制定的措施务实创新,划定的责任清晰明了,是指导全县上下抓好“两个年”活动的行动指南。刚才,*副县长和*副县长分别就“招商引资突破年”和“重大项目推进年”活动作了安排部署;县长与4家责任单位代表签订了年度工作目标责任书,*分别作了誓师发言,誓言铿锵有力、掷地有声,希望忠实践诺、真抓实干,确保年底一一兑现。与会的各位同志要认真研究“两个年”活动的相关要求,深刻领会今天会议的精神,切实抓好贯彻落实。下面,我再强调三点意见。一、把握大势、凝聚共识,坚定开展“招商引资突破年”

大班健康活动——《尖利的物品》课后反思课件教案
2、学习使用剪刀、筷子、笔、刀、游戏棒等物品的正确方法。 这节课我共分四方面来进行教学,首先让幼儿观察了解尖利物品,知道名称,了解它的用途。因为幼儿的人数较多,怕在分组活动中出现意外,所以我只准备了一份的物品让幼儿进行观察,课堂的秩序较好。在出示物品时,幼儿都能积极的举手告诉我这些物品的名称,从这里可以看出幼儿对于这些东西是十分的熟悉的;并对它们的用途也是比较了解的,大多数的幼儿一次就把所有物品的用途都说出来了,但是对于他们的共同之处幼儿的回答就不太完整,虽然知道但是不能用一个较好的词语来进行概括,从这里我发现我班幼儿在语言发展方面,词汇还是不够丰富需要加强。幼儿对‘为什么要把尖利物品设计成这样’,不太了解,有的幼儿说 “本来就是这样的”有的说“因为这样好用”……因此,在我讲了以后幼儿就有了一种恍然大捂的神情,感到很高兴,还不时和边上的同伴那进行交流。课堂的气氛一下字就活跃了起来。

【高教版】中职数学拓展模块:1.1《两角和与差的正弦公式与余弦公式》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.1两角和与差的余弦公式与正弦公式. *创设情境 兴趣导入 问题 我们知道,显然 由此可知 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 10*动脑思考 探索新知 在单位圆(如上图)中,设向量、与x轴正半轴的夹角分别为和,则点A的坐标为(),点B的坐标为(). 因此向量,向量,且,. 于是 ,又 , 所以 . (1) 又 (2) 利用诱导公式可以证明,(1)、(2)两式对任意角都成立(证明略).由此得到两角和与差的余弦公式 (1.1) (1.2) 公式(1.1)反映了的余弦函数与,的三角函数值之间的关系;公式(1.2)反映了的余弦函数与,的三角函数值之间的关系. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 启发引导学生发现解决问题的方法 25

乡镇在2024年第二季度农村人居环境整治工作总结会上的讲话
三要继续强化督查检查,建立长效机制镇人居办要常态化开展督查检查,深入一线发现问题,做到早发现、早制止、早处置,防止小问题变成大麻烦。要明确部门责任、村(街)责任,责任到人,对思想上不重视、行动上不积极、整改上不彻底的单位和个人进行通报,对在上级考核中出现严重问题的将严肃处理。人居环境整治工作既是攻坚战,也是持久战,需要我们常抓不懈、久久为功,各位要坚决克服厌战情绪和侥幸心理,牢固树立“逆水行舟,不进则退,慢进也是退”的理念,争分夺秒抓整治、全力以赴促整改,同时要保持工作韧性和连续性,杜绝“三天打鱼两天晒网”,确保长效管理不松懈、严抓共管不放松、清理彻底不反弹。同志们,人居环境整治工作既是一项民生工程,更是一项民心工程,我们既是建设者,更是受益者。

2024年某镇在第二季度农村人居环境整治工作总结会上的讲话
人居环境整治工作既是攻坚战,也是持久战,需要我们常抓不懈、久久为功,各位要坚决克服厌战情绪和侥幸心理,牢固树立“逆水行舟,不进则退,慢进也是退”的理念,争分夺秒抓整治、全力以赴促整改,同时要保持工作韧性和连续性,杜绝“三天打鱼两天晒网”,确保长效管理不松懈、严抓共管不放松、清理彻底不反弹。同志们,人居环境整治工作既是一项民生工程,更是一项民心工程,我们既是建设者,更是受益者。希望大家回去后立即部署、迅速行动、精准发力、狠抓落实,让群众切实感受到人居环境整治的热潮,以时不我待的紧迫感、舍我其谁的使命感、造福一方的责任感推动农村人居环境整治工作再上新台阶,共同把这一事关农业农村高质量发展和群众幸福生活的大事、好事抓好抓实。

镇在2024年第二季度农村人居环境整治工作总结会上的讲话
三要继续强化督查检查,建立长效机制镇人居办要常态化开展督查检查,深入一线发现问题,做到早发现、早制止、早处置,防止小问题变成大麻烦。要明确部门责任、村(街)责任,责任到人,对思想上不重视、行动上不积极、整改上不彻底的单位和个人进行通报,对在上级考核中出现严重问题的将严肃处理。人居环境整治工作既是攻坚战,也是持久战,需要我们常抓不懈、久久为功,各位要坚决克服厌战情绪和侥幸心理,牢固树立“逆水行舟,不进则退,慢进也是退”的理念,争分夺秒抓整治、全力以赴促整改,同时要保持工作韧性和连续性,杜绝“三天打鱼两天晒网”,确保长效管理不松懈、严抓共管不放松、清理彻底不反弹。同志们,人居环境整治工作既是一项民生工程,更是一项民心工程,我们既是建设者,更是受益者。

《百年风华启新程,以史为鉴创未来》国旗下的讲话范文
大家好!我是xxxx,今天我演讲的题目是《百年风华启新程,以史为鉴创未来》。 “世之奇伟、瑰怪,非常之观,常在于险远”,唯有以青春作注,不断探索开辟新发现,勇于走在时代前列,才能发现常人所目不及的新事物,才不会因虚度年华而悔恨,因碌碌无为而羞耻。 当国泰民安,丰衣足食,当国家强盛,傲视群雄,中国的青年在顺境中逆风而走,在平安中奔赴隐藏的危难。“以青春之我,创造青春之家庭,青春之国家,青春之民族”。北大90后学子宋玺,剪掉长发,穿上戎装,正姿护航亚丁湾;22岁抗疫医生李思思,用生命践行了对祖国的铮铮誓言;26岁年轻调度员高健,用一声声“北京明白”证明着征途是星辰大海…… 一代人又一代人的长征,一代人又一代人的担当。过往几代青年,皆以梦为马,以铁肩担道义,以不断探索中华之未来的脚步,铸就了如今这伟大的时代。青年的发展应该与时代环境同向而行,同频共振,时代昂扬向上的曲线,即是中国青年的生命轨迹。时间是变化的标尺,空间是更迭的参照,时空为证,见证了发展飞跃向前。每个时代有每个时代的气质,一代人有一代人的使命。但英雄从未远去,精神从不过时。无论是为抗击新冠肺炎疫情献出生命的医护人员,还是将生命定格在脱贫攻坚征程上的扶贫干部,在他们身上,同样矗立着直冲霄汉的英风浩气。

校领导在2024年XX教育工作总结表彰暨教学能力培训会上的讲话
最后,也借这个机会,向大家三点工作的要求:1.要始终秉持教学第一位的本位意识思政教育、专业教育、XX教育、知行教育、实践教育、工程教育,这些所有的模块构成了我们学校人才培养体系,大家要始终秉持教学本位的理念,深刻研判国家、社会、学校人才培养的新形势和新要求,不断探索前沿高等教育先进的教学理念和教学方法,持续推进我校教育体系的完善与创新。2.XX教育应加强团队协作XX教育建设并非闭门造车,我们在新工科新文科协同发展理念引导下,大力扶持文理渗透、理工交融的学科交叉融合,整合校内多学科资源,建立开放、共享、交叉、融合的XX教育课程体系,这已成为我们学校XX教育建设导向,所以更需要大家加强团队协作,体现产教融合科教融汇、有组织科研有组织教研的一些集中成果。3.认真践行课堂革命教学改革
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
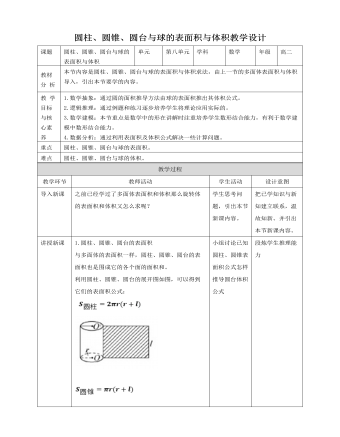
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
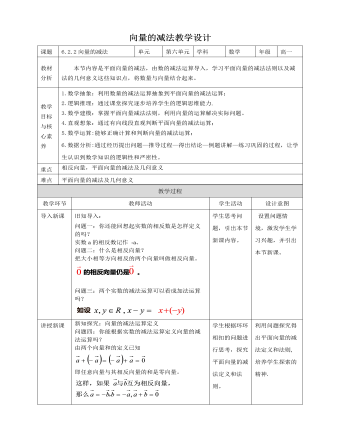
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

中班主题课件教案:筷子主题之各种各样的筷子
活动目标:1、通过看看、摸摸、玩玩使幼儿辨认各种筷子,了解筷子的特点与用途,并学习归类。2、让幼儿练习使用筷子,初步学会拨、夹物品,做到持筷姿势正确。活动准备:幼儿自带的不同材料制成的筷子、每组上面一样夹的物品(如:一组蚕豆、一组泡漠、一组花生、一组玻璃球、一组纸条等。活动过程:㈠、观察各种各样的筷子,将幼儿所带筷子布置成展览会。1、看看桌子上有什么?我们来把它布置成展览会。2、交流:你带的筷子是什么样的?叫什么名字?有什么用处?

大班体育综合训练活动“可爱的小青蛙”课件教案
2、让幼儿在活动中体验合作的乐趣,培养他们解决问题、克服困难的好品质,激发幼儿的团队精神。活动准备:竹筐20个(边筐高25厘米)、4张圆形大小不一的荷叶、纸皮(荷叶)每人一张活动过程:一、准备活动1、 音乐游戏“小青蛙醒来了”。教师与幼儿随着音乐做各种动作,活动身体。2、 幼儿每人选一张“荷叶”,摆在地上,进行跳进跳出动作练习,(教师提醒幼儿注意起跳时先屈膝,落地要轻)

初中语文《阿西莫夫短文两篇- 被压扁的沙子》试讲稿_教案设计
质疑问难,合作探究 1、文章是介绍沙子的知识吗? 明确: 有关恐龙灭绝的原因,原来本文的主角不是沙子,而是恐龙。 2、题目是《被压扁的沙子》,内容却恐龙灭绝的原因,题目《被压扁的沙子》是否偏离主题了?我们换成《恐龙是怎样灭绝的》会不会更好? 本文题目不但没有离题,还能提示读者,恐龙灭绝的“撞击说”所以产生,与被压扁的沙子的科学发现和科学研究密不可分此外,文题形象性强,容易激起好奇心,引起人们的阅读兴趣 3、恐龙灭绝的原因一直是学术界有争议的问题,因而产生两种学说“撞击说”“火山说”在探究恐龙灭绝的原因时,作者的观点是什么?他的观点以什么为依据,又是怎样推论出来的?



