-

LOGO(标志)设计委托合同书
依据《中华人民共和国合同法》和有关法规的规定,乙方接受甲方的委托,就公司LOGO(标志)设计或公司产品商标设计事项,双方经协商一致,签订本合同,信守执行:一、委托之事项:甲方委托广州有易信息科技有限公司为其公司设计标志 个。二、委托设计费用:公司标志设计单价为人民币11000元,总价为:人民币______________元(大写:______________________)三、付款方式:1、甲方需在合同签订之日起两个工作日内将标志设计的30%款项汇入乙方帐户,乙方收到甲方款项后开始制作设计任务。2、标志确认后,甲方再支付项目余款。四、乙方设计作品的时间、交付方式:1、乙方需在 个工作日内设计出甲方公司的标志初稿。并在 工作日内完成本项目交付。2、乙方以电子稿交付方式交付设计的作品,乙方在收到甲方余款结清后一个工作日内通过网络或邮寄的方式把标志电子稿交予甲方。五、知识产权约定:1、乙方对设计完成的作品享有著作权。甲方将委托设计的所有费用结算完毕后,作品著作权自动转让给甲方。2、甲方在未付清所有委托设计费用之前,乙方设计的作品著作权归乙方,甲方对该作品不享有任何权利。3、甲方在余款未付清之前擅自使用或者修改使用乙方设计的作品而导致的侵权,乙方有权依据《中华人民共和国著作权法》追究其法律责任。

标志设计委托合同书
甲方:乙方:xxxx商标代理有限公司依据《中华人民共和国合同法》和有关法规的规定,乙方接受甲方的委托,就公司标志设计或公司产品商标设计事项,双方经协商一致,签订本合同,信守执行:一、委托之事项:甲方委托xxxx商标代理有限公司为其公司设计标志 个。具体内容为 。二、委托设计费用:公司标志设计单价为人民币_______元。总价为:人民币______________元,(大写:______________________)三、付款方式:1、甲方需在合同签订之日起两个工作日内将委托设计总费用的70%通过电汇或银行转账到乙方公司帐户(乙方收到甲方的银行划帐凭据后作为标志设计的开始时间)。2、标志设计完成后,甲方需在三天内签名或盖章确认(以传真方式确认同样有效),确认后甲方应当即付标志设计费用的全部余款。四、乙方设计作品的时间、交付方式:1、乙方需在七个工作日内设计出甲方公司的标志初稿。单个标志设计完成的时间为10个工作日左右。2、乙方以电子稿交付方式交付设计的作品,乙方在收到甲方余款结清后的有关凭据后一个工作日内通过网络或邮寄的方式把标志电子稿交予甲方。

标志设计委托合同书
依据《中华人民共和国合同法》和有关法规的规定,乙方接受甲方的委托,就_______标志设计事项,双方经协商一致,签订本合同,信守执行:一、委托之事项:甲方委托xxx广告设计有限公司为其公司设计标志 个,公司产品商标 个。二、委托设计费用:公司标志设计单价为人民币_______元,公司产品商标设计单价为人民币_______元;总价为:人民币______________元,(大写:______________________)三、付款方式:1、甲方需在合同签订之日起两个工作日内将委托设计总费用的50%通过现金方式或银行转账到乙方公司帐户(乙方收到甲方的银行划帐凭据后作为标志设计的开始时间)。2、标志初稿提交时,甲方须支付合同总额的30%作为第二期款项,标志设计完成后,甲方需在三天内签名或盖章确认(以传真方式确认同样有效),确认后甲方应当即付标志设计费用的全部余款。四、乙方设计作品的时间、交付方式:1、乙方需在七个工作日内设计出甲方公司的标志初稿。单个标志设计完成的时间为15个工作日左右。

(广厦建工)标志设计合同
甲方:xxx安装工程有限公司 乙方:xxx广告装饰有限公司依据《中华人民共和国合同法》和有关法律、法规规定,乙方接受甲方的设计,就设计相关事项,双方经协商一致,签订本合同,信守执行: 一、委托设计事项:甲方委托乙方为其设计“(广厦建工)标志”。二、设计费用:设计费用总计为:人民币2600元 (大写:贰仟陆佰元整)。三、付款方式:甲方需在合同签订之日起15个工作日内,向乙方支付设计全款,付款方式为一次性现金支付或转账。四、设计交付方式:1、乙方自合同签订之日起15日内,以电子稿形式向甲方交付设计方案。

网店设计外包合同
甲乙双方经协商一致,本着诚实信用、互利互惠的原则,依据《中国人民共和国合同法》,以及相关法规的规定,就甲方网页网店项目设计工作外包一事达成如下协议:一、 乙方接受甲方委托,完成甲方正在开发的项目中的网页网店设计工作,本外包合同中所指项目“网页网店设计工作”,是指与本项目相关的一切设计设计、制作工作。二、网店设计外包收费标准及注意事项1.页面收费标准:店铺首页、装修自定义页面、活动承接页 350/页/次(html静态页面包切片)2.单品收费标准:详情页面设计(不含拍摄):统一模版150/款 (含详情焦点图1张) 非统一模版250/款 (含详情焦点图2张)3.焦点广告图50/张 钻石展位、聚划算、直通车 150/张4.设计作品定稿上传后不支持再改,否则将视为重新设计。三、双方权利及义务1、乙方托管服务方式:远程为客户操作(不提供上门服务)

企业标志设计服务合同
为了更好的塑造符合企业的视觉形象,甲方委托乙方进行企业的标志设计工作,甲乙双方秉承相互促进,相互信赖的原则,经友好协商,达成如下协议:一、合同内容企业标志标志墨稿反白效果稿标准化制图企业标准字体企业全称中文字体(简体)企业简称中文字体(简体)企业全称英文字体企业简称英文字体标准英文字体坐标制图企业标准色(印刷色)辅助色系列 名片便签合同书封面手提袋形象墙名牌二、费用设计(不含税)总费用为人民币 10000 元(大写 壹万 元整)。 此费用不含甲方申请商标注册费用,及不含与商标注册相关的所有费用。 三、付款方式 1、本合同签订后,甲方向乙方支付合同总费用50%,即人民币 5000 元(大写: 伍仟 元整)作为预付款; 2、项目设计完成经甲方认可确认,甲方即向乙方支付合同余款,即人民币 5000 元(大写: 伍仟 元整)。乙方在收到款项的一个工作日内,向甲方提交电子文件光盘。 四、设计时间商标设计系统设计工作分为二个阶段完成,共 14 个工作日(不含甲方校稿时间)第一阶段:乙方收到甲方所支付预付款后 7 天,设计标志初稿交甲方认可。 第二阶段: 7 天,修改标志及完成应用设计。 五、双方的责任与义务甲方权利:1、甲方有权对乙方的设计提出建议和思路,以使乙方设计的设计更符合甲方企业文化内涵;2、甲方有权对乙方所设计的商标提出修改意见。

XXX效果图设计合同
根据《中华人民共和国广告法》,《中华人民共和国合同法》及国家有关法律、法规的规定,甲、乙双方在平等、自愿、等价有偿、公平、诚实信用的基础上,经友好协商,就甲方委托乙方设计、制作 效果图事宜,达成一致意见,特签订本合同,以资信守。第一条 委托事项(具体见 )第二条 合同总价款及付款方式1、本合同设计费单价为人民币 元(大写: ),输出打样等其他费用为人民币 元(大写: ),暂定总价款为人民币 元(大写: ),按实验收结算。前述费用已包括税费、设计费、输出及打印等一切费用,若甲方有特殊要求,甲乙双方应另行协商。2、本合同签订后 个工作日内,甲方应向乙方支付合同总价款的 %,即人民币(大写): 作为预付款。3、乙方交付设计成果经甲方验收达到合同约定的设计要求和验收标准后 个工作日内,甲方向乙方支付合同结算余款。4、以上付款,甲方将以转帐支票或电汇的方式支付,若甲方提出按六个月的承兑汇票支付的,则按开票银行同期贴现利息补息。付款时,乙方须向甲方开具中华人民共和国大陆地区合法有效的等额发票,否则甲方可顺延付款。
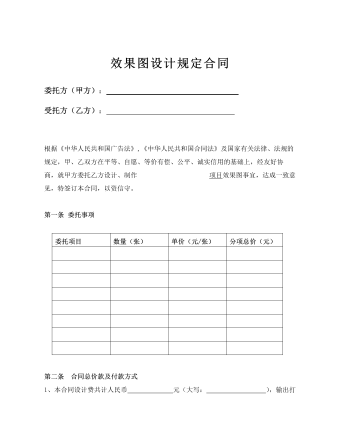
效果图设计规定合同
根据《中华人民共和国广告法》,《中华人民共和国合同法》及国家有关法律、法规的规定,甲、乙双方在平等、自愿、等价有偿、公平、诚实信用的基础上,经友好协商,就甲方委托乙方设计、制作 项目效果图事宜,达成一致意见,特签订本合同,以资信守。第一条 委托事项委托项目 数量(张) 单价(元/张) 分项总价(元)第二条 合同总价款及付款方式1、本合同设计费共计人民币 元(大写: ),输出打样等其他费用为人民币 元(大写: ),总价款为人民币 元(大写: )。前述费用已包括税费,如有需要增加新角度,则在补充合同上另行商定。2、本合同签订后1个工作日内,甲方应向乙方支付合同总价款的50%,即人民币(大写): 。3、乙方交付设计成果后当日内,甲方向乙方支付合同结算余款。第三条 双方义务1、甲方负责在约定的时间内提供乙方设计所需的项目详细资料,且乙方仅需在甲方提供的资料范围内制作效果图,如超出制作效果图范畴的应按照设计费计算方式结算制图费,并对其所提供的资料的合法性负责:2、甲方应按合同约定向乙方支付本合同价款。

室内精装修设计合同范本
依据《中华人民共和国合同法》和相关法规的规定,乙方接受甲方的委托,就_______________________设计事项,双方经协商一致,签订本合同,信守执行。一、合同内容及要求:二、设计费用:设计费用为_________每平米,共_________平米,总计为:人民币¥______________元,(大写:_______________元整)。三、付款方式:1、甲方需在合同签订时付委托设计与制作总费用的50%即人民币¥_________元(大写:_________________)。2、乙方将设计制作印刷品交付甲方时,甲方需向乙方支付合同余款,即人民币¥______________元(大写:_________________)。四、设计与制作作品的时间及交付方式:1、设计期限:________年____月_____日至________年_____月____日止2、乙方需在双方约定的时间内完成设计方案。因甲方反复提出修改意见导致乙方工作不能按时完成时,可延期执行,延期时间由双方协商确定。五、知识产权约定:1、甲方在未付清所有委托设计制作费用之前,乙方设计的作品著作权归乙方,甲方对该作品不享有任何权利。2、甲方将委托设计制作的所有费用结算完毕后,甲方拥有作品的所有权、使用权和修改权。

装饰装修设计合同
设计期限为 天,从乙方收到甲方支付的定金后开始计算,到向甲方交付全套设计图纸之日为止。因甲方变更设计要求或对乙方意见未及时答复,其耽误的时间应从合同约定的设计期限中相应扣除。2.设计交图步骤及时间:(1)甲、乙双方当面协商满意后确定设计详细内容及金额,即签定本合同,同时支付定金人民币 元。乙方收到定金后 天内,向甲方提交装修设计方案图及平面功能定位图,如乙方未提交装修设计方案图及平面功能定位图,则双倍向甲方返还定金。 (2)甲、乙双方初步确定平面方案及初步确定设计概念后,同时支付首期设计费人民币 (按以上2(1)支付的人民币定金自动转为首期设计费)。乙方收到设计费后 天内,向甲方提交较详细装修设计方案包括主要立面图。(3)甲方确认立面方案、天花方案即支付第二期设计费人民币,乙方收到设计费案后 天内,向甲方提交详细装修施工图及效果图。(4)甲方签字确认设计施工图后即支付第三期设计费人民币,乙方向甲方提供全套正式设计施工图纸。 (5)工地开工后设计师配合施工队现场指导并对业主提供材料及工程质量咨询服务。

室内精装修设计合同
第一条 定义除上下文另有要求外,以下各词和用语,应具有如下的涵义:1.1 “适用法律”指在中华人民共和国和长沙市已颁布并生效的具有法律效力的法律和其它文件。1.2“服务”指本协议设计任务书所述的,按照协议由乙方完成本项目而进行的工作。1.3 “货币”指人民币元,本协议另有约定的除外。第二条 解释合同文件的组成及优先顺序:(1) 本合同协议(由标准及特殊条件、担保条款(如有)三部分组成)及附件(2) 经甲方认可的乙方承诺(3) 招标文件及其附件(如有)(4) 投标书及其附件(如有)(5) 中标通知书(6) 标准、规范及有关技术文件第三条 项目概况及服务内容、标准3.1 项目概况及服务内容、标准等见第二部分规定。3.2甲方为建造本项目所需要的设计服务的任何内容,并不会因为本协议的局限而被视为遗漏,乙方保证在规定的期限内按质按量完成规划部门、政府相关部门和甲方所需的全部设计文件。第四条 设计服务费4.1 本协议设计服务价格总额及费用明细见第二部分的规定。4.2 本协议第4.1条规定的设计服务价格总额为固定价格,该价格包括所有人员费用、印刷打印出图、电子版图纸刻录费用、通讯、差旅、交通、设计补充完善等所有在乙方执行本协议所述的服务中发生的全部费用。除非另有规定,否则此价格不以任何理由改变。

室内精装修设计合同
精装修住宅正成为一种发展趋势,那么室内精装修设计合同是怎样的呢?以下是为大家精心整理的室内设计精装修合同,欢迎大家阅读,供您参考。更多内容请关注。 室内精装修设计合同(一) 甲方: 乙方: 依据《中华人民共和国合同法》和有关法规的规定,乙方接受甲方的委托,就_______________________设计事项,双方经协商一致,签订本合同,信守执行。 一、合同内容及要求: 二、设计费用: 设计费用为_________每平米,共_________平米,总计为:人民币¥______________ 元,(大写:_______________元整)。三、付款方式: 1、甲方需在合同签订时付委托设计与制作总费用的50%即人民币 ¥ _________ 元(大写:_________________)。 2、乙方将设计制作印刷品交付甲方时,甲方需向乙方支付合同余款,即人民币¥______________元(大写:_________________

小学讲诚信懂礼仪公民教育实践活动教学教案
二、教学过程:1、活动一:讲故事,学诚信。1)师:春秋战国时期,商鞅下令在都城南门外立一根三丈长的木头,并许下诺言:谁能把这根木头搬到北门,赏金十两。有人将木头扛到了北门,商鞅立即赏了他五十金。商鞅这一举动,在百姓心中树立起了威信。而商鞅接下来的变法就很快在秦国推广开了,新法使秦国渐渐强盛,最终统一了中国。
人教版新课标小学数学六年级上册统计教案
【新知识点】认识扇形统计图统计填写扇形统计图根据扇形统计图所提供的数据回答问题【单元教学目标】1,认识扇形统计图,了解扇形统计图的特点.2,能够看懂并会填扇形统计图.3,会根据扇形统计图所提供的数据回答一些简单的问题.4,进一步了解统计在实际生活中的地位和作用.5,通过对相关素材的整理和分析,使学生受到一定的思想教育.【单元教学重难点】重点:学生掌握扇形统计图的特点和作用.难点:在学习中体会各种统计图的不同特点.【教学建议】学生已经系统地学习过有关条形统计图和折线统计图的知识,也初步认识了扇形,而且也学习了有关百分数的知识,所有这些都为学校继续学习统计图的最后一部分内容——扇形统计图打下了良好的基础.【课时安排】

双曲线的简单几何性质(1)教学设计人教A版高中数学选择性必修第一册
问题导学类比椭圆几何性质的研究,你认为应该研究双曲线x^2/a^2 -y^2/b^2 =1 (a>0,b>0),的哪些几何性质,如何研究这些性质1、范围利用双曲线的方程求出它的范围,由方程x^2/a^2 -y^2/b^2 =1可得x^2/a^2 =1+y^2/b^2 ≥1 于是,双曲线上点的坐标( x , y )都适合不等式,x^2/a^2 ≥1,y∈R所以x≥a 或x≤-a; y∈R2、对称性 x^2/a^2 -y^2/b^2 =1 (a>0,b>0),关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴,原点是对称中心,又叫做双曲线的中心。3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点 .顶点是A_1 (-a,0)、A_2 (a,0),只有两个。(2)如图,线段A_1 A_2 叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段B_1 B_2 叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长。(3)实轴与虚轴等长的双曲线叫等轴双曲线4、渐近线(1)双曲线x^2/a^2 -y^2/b^2 =1 (a>0,b>0),的渐近线方程为:y=±b/a x(2)利用渐近线可以较准确的画出双曲线的草图

抛物线的简单几何性质(1)教学设计人教A版高中数学选择性必修第一册
问题导学类比用方程研究椭圆双曲线几何性质的过程与方法,y2 = 2px (p>0)你认为应研究抛物线的哪些几何性质,如何研究这些性质?1. 范围抛物线 y2 = 2px (p>0) 在 y 轴的右侧,开口向右,这条抛物线上的任意一点M 的坐标 (x, y) 的横坐标满足不等式 x ≥ 0;当x 的值增大时,|y| 也增大,这说明抛物线向右上方和右下方无限延伸.抛物线是无界曲线.2. 对称性观察图象,不难发现,抛物线 y2 = 2px (p>0)关于 x 轴对称,我们把抛物线的对称轴叫做抛物线的轴.抛物线只有一条对称轴. 3. 顶点抛物线和它轴的交点叫做抛物线的顶点.抛物线的顶点坐标是坐标原点 (0, 0) .4. 离心率抛物线上的点M 到焦点的距离和它到准线的距离的比,叫做抛物线的离心率. 用 e 表示,e = 1.探究如果抛物线的标准方程是〖 y〗^2=-2px(p>0), ②〖 x〗^2=2py(p>0), ③〖 x〗^2=-2py(p>0), ④

双曲线的简单几何性质(2)教学设计人教A版高中数学选择性必修第一册
二、典例解析例4.如图,双曲线型冷却塔的外形,是双曲线的一部分,已知塔的总高度为137.5m,塔顶直径为90m,塔的最小直径(喉部直径)为60m,喉部标高112.5m,试建立适当的坐标系,求出此双曲线的标准方程(精确到1m)解:设双曲线的标准方程为 ,如图所示:为喉部直径,故 ,故双曲线方程为 .而 的横坐标为塔顶直径的一半即 ,其纵坐标为塔的总高度与喉部标高的差即 ,故 ,故 ,所以 ,故双曲线方程为 .例5.已知点 到定点 的距离和它到定直线l: 的距离的比是 ,则点 的轨迹方程为?解:设点 ,由题知, ,即 .整理得: .请你将例5与椭圆一节中的例6比较,你有什么发现?例6、 过双曲线 的右焦点F2,倾斜角为30度的直线交双曲线于A,B两点,求|AB|.分析:求弦长问题有两种方法:法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为

用空间向量研究距离、夹角问题(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、点到直线的距离、两条平行直线之间的距离1.点到直线的距离已知直线l的单位方向向量为μ,A是直线l上的定点,P是直线l外一点.设(AP) ?=a,则向量(AP) ?在直线l上的投影向量(AQ) ?=(a·μ)μ.点P到直线l的距离为PQ=√(a^2 "-(" a"·" μ")" ^2 ).2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.点睛:点到直线的距离,即点到直线的垂线段的长度,由于直线与直线外一点确定一个平面,所以空间点到直线的距离问题可转化为空间某一个平面内点到直线的距离问题.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 . 答案: √174/6解析:如图,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),E(0,2,1),F(1,0,2),(EF) ?=(1,-2,1),

用空间向量研究直线、平面的位置关系(1)教学设计人教A版高中数学选择性必修第一册
二、探究新知一、空间中点、直线和平面的向量表示1.点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量(OP) ?来表示.我们把向量(OP) ?称为点P的位置向量.如图.2.空间直线的向量表示式如图①,a是直线l的方向向量,在直线l上取(AB) ?=a,设P是直线l上的任意一点,则点P在直线l上的充要条件是存在实数t,使得(AP) ?=ta,即(AP) ?=t(AB) ?.如图②,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使(OP) ?=(OA) ?+ta, ①或(OP) ?=(OA) ?+t(AB) ?. ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.1.下列说法中正确的是( )A.直线的方向向量是唯一的B.与一个平面的法向量共线的非零向量都是该平面的法向量C.直线的方向向量有两个D.平面的法向量是唯一的答案:B 解析:由平面法向量的定义可知,B项正确.

空间向量及其运算的坐标表示教学设计人教A版高中数学选择性必修第一册
一、情境导学我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.二、探究新知一、空间直角坐标系与坐标表示1.空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.

