-

关于参加网络教育培训学习个人心得体会八篇
现在很多软件为了自身盈利的需要而夹杂了流氓软件,流氓软件安装之后又是极不容易卸载的。这些流氓软件可能会修改你的浏览器主页,定期打开某一网页等等,造成了我们使用电脑时的极大不便,这些软件还会记录下我们上网偏好,随时向我们发垃圾广告。所以下载安装软件一定要慎重。第三慎用U盘、移动硬盘之类的存储设备。某些破坏性的病毒可能导致移动存储设备损坏。我们在使用U盘之类的存储设备时也要小心谨慎,打开U盘时尽量不要双击打开,这样很可能会激活存在于里面的木马,使用打开前最好能够先杀一遍毒,甚至我们可以专门去网上搜取U盘木马专杀来预防电脑再次被感染。第四尽量不要在互联网上公布个人信息。除非是万不得已,否则不要公布自己任何详细的信息,以防被不良分子利用。另外在网上不要随意公布自己的邮箱,因为邮箱是一个十分便利的切入口来搜取你的个人信息,我们在各个网站注册时一般都会被要求留下邮箱,这样在这个过程中或多或少我们都会偷漏一些个人信息,如果通过搜取邮箱的方法获得你在各个网站上公布的个人信息经过综合整理很可能是自己更多的信息被公布出来。更多的我们考虑的自身安全问题,公布照片不仅使我们信息安全得不到保护,甚至现实中我们人身安全也可能因为一张照片而受到威胁。

有关教师个人学习职业道德规范心得体会优选例文
第三,要奉献爱心。崇高的师爱表现在对学生一视同仁,绝不厚此薄彼,按成绩区别对待。要做到“三心俱到”,即“爱心、耐心、细心,”无论在生活上还是学习上,时时刻刻关爱学生,特别对那些学习特困生,更要付出特殊的关爱,切忌言行过激、办事草率。对学生细微之处的改变也要善于发现,发现他们“闪光点”,并且多加鼓励,培养学生健康的人格,树立学生学习的自信心,注重培养他们的学习兴趣。 第四,要以身作则。教师的一言一行、一举一动对学生的思想、行为和品质具有潜移默化的影响,学生们都喜欢模仿。为此,教师一定要时时处处为学生做出榜样,凡是教师要求学生要做到的,自己首先做到;凡是要求学生不能做的,自己坚决不做。只有严于律已,以身作则,诲人不倦,才能让学生心服口服,才能把教师当成良师益友。

关于校园开展安全教育培训个人心得体会八篇
学校是培养人的场所,是社会知识和智慧的中心,是国家发展的希望所在,然而学生生活的环境中的.不安全隐患比比皆是,学生伤害事故更是频频发生,不仅给学生本人及其家长带来了无可挽回的痛苦和损失,而由此引起的纠纷更是纠缠不清,往往带来巨大困扰。甚至影响正常教育教学。安全责任重于泰山,各校均把安全教育放在重中之重的位置,学校领导大会小会强调安全,老师课前课中课后讲安全,可以说学校教师时时刻刻都绷紧了安全这根弦。家长也千叮咛万嘱咐。尽管如此,学生的安全意识仍然很淡薄,安全事故总有发生。为什么会出现这样的状况呢?

关于镇街中层及以下干部队伍建设的调研报告范文
(一)结构不够优。一是年龄结构不合理,编内人员(公务员和事业编制人员)年龄在*周岁以下的只有*人,占编内人员*%。二是学历偏低,学历为全日制大专及以下的有*人,占*%,硕士研究生只有*人;三是专业化水平不高,具有专业技术职称的只有*人,占比*%,其中工程师职称只有*人,难以适应专业化、高质量工作的需求。作为中坚力量的*名中层干部中,大专及以下学历占*%,专业型干部不足*%,编外人员占一半以上。

高中部第三周升旗仪式国旗下讲话稿:爱在三月,情暖校园
尊敬的老师、亲爱的同学们:大家早上好,我是来自高二六班的张昊宇,今天我国旗下讲话的题目是《爱在三月,情暖校园》。三月,有一种充满生机的希望在流淌;三月,有一种炽热的情愫在弥漫;三月,有一种深切的怀念在升腾。在这乍暖还寒的日子里,让我们行动起来,用绵外人的特有的热情去消融最后的寒意吧!让爱心在三月传递,让温情在校园洋溢,让我们用以下几个词去书写多彩的三月吧。第一个词是奉献。当春风吹绿大地,万物吐露芬芳之时,我们总会想起一个如阳光般温暖的名字―雷锋。3月5日,是“学雷锋纪念日”,同时也是“青年志愿者服务日”,让我们行动起来,向雷锋学习吧!给人一个微笑,不经意间,温暖一颗心灵;拾起一张纸片,不经意间,守护一片洁净;关掉一个开关,不经意间,增添一份光彩。阳光之所以明媚,正是无数束小光线凝集而撒向大地的结果,也许我们的行为微不足道,也许我们的行为并不引人瞩目,但只要我们携起手来,从我做起,从身边做起,就能让成千上万个雷锋成长起来!第二个是感恩。漫漫人生路,我们只有一个母亲,却有太多的“母爱”。在家里,母爱是儿时甜甜的吻、是清晨路上的几句叮咛、是眼角两旁的一条皱纹、是秋风吹散的一缕白发……在学校,母爱是润物无声教会我们打开知识大门的钥匙,是不辞劳苦帮助我们扬起理想风帆的桅杆,是无微不至拨开我们心灵阴霾的春风……

(10篇)推进干部能上能下工作经验材料总结汇报报告
二、强化日常分析研判,让能“上”能“下”有理由通过日常考核考察、专项调研、监督检查等方式,对干部队伍及干部个人进行综合分析研判,2021年乡镇领导班子换届中,通过充分比选酝酿,选拔x名优秀干部进入乡镇领导班子,对x名工作能力与岗位需求不相匹配的干部及时进行调整。注重将工作实绩与干部能“上”能“下”有机结合,每季度对各单位牵头负责的省、州、市重点项目和工作任务推进情况进行全面督办,根据推动落实情况进行定星评级,在市行政中心门口以大型展板向全市人民公示,并将其作为年度综合目标考核等次评定的重要依据,同时作为干部评优评先、提拔晋升和调整履职不力、本职工作推进较差的干部“下”的重要依据。三、全面落实严管厚爱,让能“上”能“下”有措施构建“四位一体”从严管理干部机制,整合纪检、组织、机构编制、考评部门职能职责资源,印发《x市建立工作目标、岗位责任、正向激励保障、负向惩戒约束“四位一体”从严管理干部机制实施方案》,针对干部正向激励保障和负面惩戒约束提出x条措施,着力将干部管理落细落实落在经常,推动干部能“上”能“下”科学化、规范化,为高质量建设强富美的新x提供了有力的组织保证。

在领导干部个人有关事项报告专题培训会上的讲话
这次专题培训,就是进一步提高认识,打牢思想基础,学好学通政策规定,杜绝人为失误。待会儿,XXX同时将结合两项法规,就领导干部个人有关事项报告查核结果处理案例专题讲解。组织部要带头学深学透、精通政策,切实发挥好指导、服务、帮助作用。全体处级干部要认真领会,要原原本本、逐字逐句认真研读两项法规精神和《领导干部个人有关事项报告表》各项内容,确保报告内容全面、真实、准确,符合规定要求。

公司领导干部轮岗个人工作总结集团企业述职报告汇报
三、担当筹备主责,无缝隙对接建设、营运我主动分担xx领导班子工程建设压力,牵头负责营运筹备工作。一是把握大局,制定筹备、并网等工作方案。成立领导及工作小组,倒排工作计划,有序推进各项工作顺利开展。二是综合协调,完成通车各类政策性文件审批。协调省交通厅、发改委、交通部路网中心及地方单位,完成收费站开通、费率核算、路政大队成立等xx余项工作审批。三是建章立制,保障通车收费平稳过渡。制定实施了收费管理办法、收费作业规程等xx部系列制度及预案,确保通车收费有章可循,有据可依。四是加强培训,提升新员工业务水平。组织开展xx名新员工入职培训,举办收费、监控等各类业务培训xx次,共xx人次。五是狠抓落实,有序推进筹备系列工作。每周召开工作推进会;深入现场,靠前指挥,督促各项工作落到实处。及时沟通房建、机电等部门,提出合理化建议xx多条,实现建设与运营无缝对接。

新版防汛应急预案方案
二、突出重点,保障统筹推进救助工作。由副镇长罗东梅牵头,社会事务办公室具体负责,镇财政划拨专项救助资金统筹安排好群众救助工作,并落实好大渡中小学安置点的值班人员以及群众的生活安排,保证群众有房住有饭吃有衣穿。同时,加强防汛善后知识食品卫生知识等知识宣传。清淤工作。由镇长刘国荣负责牵头,镇长助理余子云具体负责,整治办负责具体落实,每天至少组织100人参与清淤工作,保证在最快的时间完成全部的清淤工作。防疫工作。由副镇长罗东梅牵头,卫生院院长龙坤组织落实,每天至少组织10人以上的消毒队伍,对全部区域进行消毒,做到彻底不留死角。

XX年下学期读书节国旗下讲话稿
亲爱的老师、同学们,大家好!随着忙碌的九月份的结束,我们内涵丰富,精彩纷呈的体育节顺利落下帷幕。湘郡的校园生活是由一个个充满挑战和快乐的日子组成,我们在这里锻炼,在这里成长。金秋十月,我们又迎来了“书香校园,筑梦未来”的读书节。我们的郡园,一直以来都有着浓浓的书香气息,读书的画面随处随时可见:早晨,同学们在操场捧着书本认真学习;银杏树下留下了同学们专心阅读的背影;林荫小道的长凳也是同学们阅读的好地方;更不用说在老师指导下,坐在教室、阅览室细细品读的情景......读书多的人,必然就会慢慢优秀起来,本学期,我们已进行了两次征文活动,我也有幸读到了参选同学的许多好:文笔优美,立意深远,动人心弦。透过涓涓文字,可以感受到小作者们才情了得,各有千秋,如1504班的伍润莲同学对宋词如数家珍;1508班的柏杭同学关于梦想,有他自己的独到见解;1505班周于韬同学对诸葛亮精神的精彩解读;1602鞠帆对乡愁的细细吟唱......

年会策划方案
公司的年会上都会有公司的员工参与或编排的表演。可以请来专业的老师进行指导并协助编排节目。(曾经有一个公司的年会因当年最为流行的是“超级女生”,几个唱歌比较好的女孩子组合在一起,彼此做了一个定位后形成了“超级女生Copy版”。

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
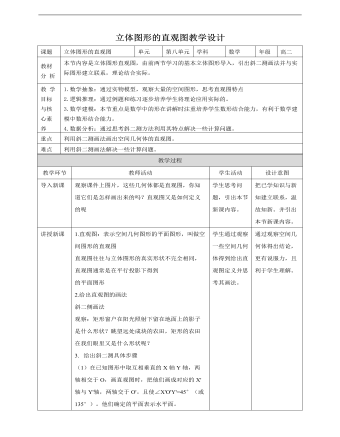
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
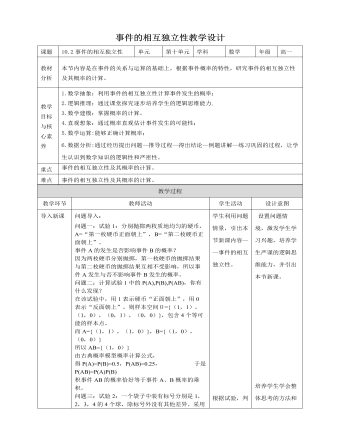
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
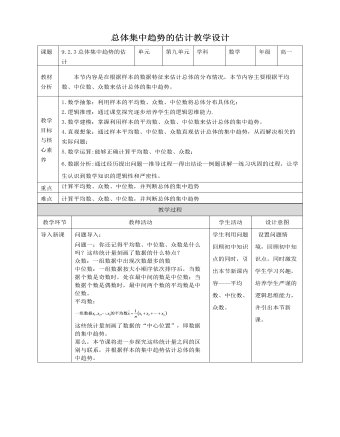
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。
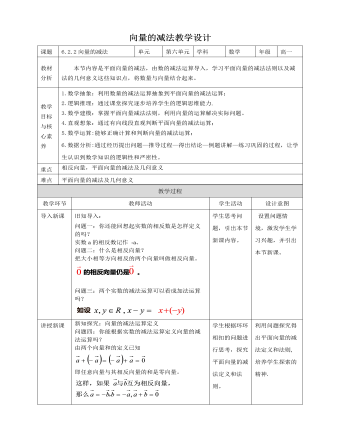
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )



