-

人教A版高中数学必修一指数函数的概念教学设计(2)
指数函数与幂函数是相通的,本节在已经学习幂函数的基础上通过实例总结归纳指数函数的概念,通过函数的三个特征解决一些与函数概念有关的问题.课程目标1、通过实际问题了解指数函数的实际背景;2、理解指数函数的概念和意义.数学学科素养1.数学抽象:指数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用指数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结指数函数概念.重点:理解指数函数的概念和意义;难点:理解指数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入在本章的开头,问题(1)中时间 与GDP值中的 ,请问这两个函数有什么共同特征.要求:让学生自由发言,教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修二立体图形直观图教学设计
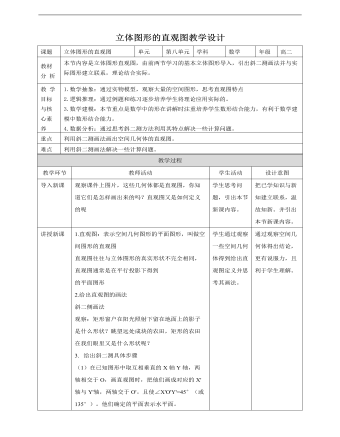
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
人教A版高中数学必修二平面与平面平行教学设计
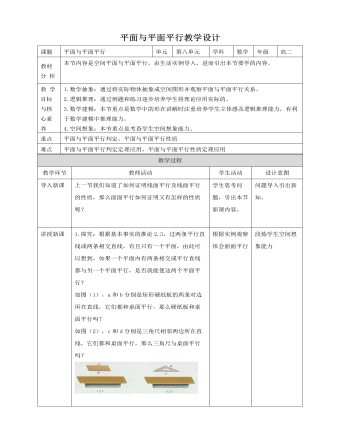
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二事件的相互独立性教学设计
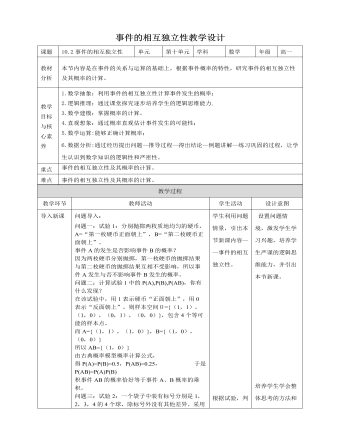
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
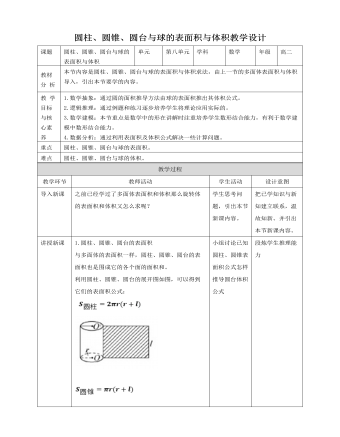
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二向量的减法运算教学设计
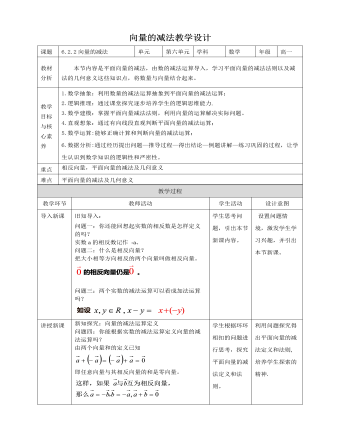
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
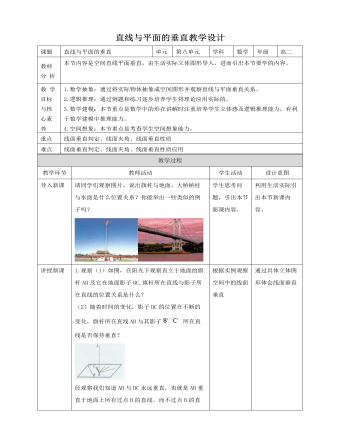
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
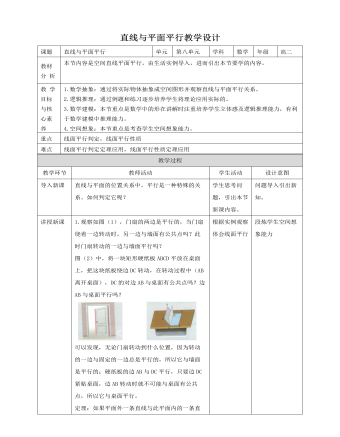
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

“文明礼仪教育”国旗下讲话稿:争做文明扬帆小使者
敬爱的老师,亲爱的同学们:大家早晨好!今天,我在国旗下讲话的题目是——争做文明扬帆小使者。文明是一个非常大的概念,我们今天就其中的礼仪方面一起来聊一聊。说到礼仪,对一个国家来说,是文明程度、道德风尚的反映;对一个人来说,是思想道德、文化修养的外在表现。礼仪的内容涵盖很多方面,有仪容、举止、表情、服饰、谈吐的礼仪;还有个人礼仪、公共场所礼仪、餐桌礼仪、文明交往礼仪等等。礼仪内容丰富多样,但它也有规律性,主要有四项原则:一是敬人原则,即尊敬别人;二是自律原则,就是自己约束好自己;三是适度的原则,适度得体,掌握分寸;四是真诚的原则,以诚待人,言行一致。上学期,我们xx小学的扬帆娃们在问候礼仪方面有了很大的进步,而且任然保持到了这学期,这样一个良好礼仪的长久坚持,就是一种文明礼仪好习惯的养成。礼仪无处不在,那么我们xx小学的扬帆娃应该怎样做,才能进一步彰显文明礼仪呢?

“文化遗产日”国旗下讲话稿:中国传统文化的艺术珍品
敬爱的老师们,亲爱的同学们,大家上午好!我是来自高二、七班的龚xx。今天我演讲的主题是“中国传统文化的艺术珍品”。不知大家闲暇时有什么爱好?我最爱画得桃红柳绿的花旦玉兰指一压唱一曲《牡丹亭》。牡丹亭属于昆曲。昆曲,又称昆剧、昆腔、昆山腔,是中国最古老的剧种之一,也是中华传统文化艺术中的珍品。十四世纪中叶,元代末期,昆曲发轫于吴语系的昆山。十五年前的5月18日,这对大多数昆曲爱好者而言是一个特殊的日子。昆曲在XX年5月18日被联合国教科文组织列为“人类口述非物质文化遗产代表作”。从昆曲开始,中国传统文化逐渐走向世界的舞台,此后共有31项文化遗产申遗成功。与昆曲属于同一文化体系的,有柳暗花明,曲径通幽的苏州园林艺术,有巧夺天工,色彩明丽的苏州刺绣,他们都是江南文化的精髓。

第十周国旗下讲话稿:践行文明,创建和谐、文明校园
今天我演讲的题目是《践行文明,创建和谐、文明校园》。我国是一个有着几千年历史的文明古国,素以“礼仪之邦”著称。然而在岁月的长河中,我们的祖国历经磨难,又涅盘新生,可以说如今大家是腰包“鼓起来”,生活“阔起来”,远离了物质的窘迫,却又浑然不觉地陷入“发展的列车匆匆驶过精神站台,现实的变化把心灵的地图抛在身外”的另一种窘境中。恩格斯说:“国家是文明社会的概括。”作为社会主义核心价值观的关键词汇,“文明”折射着一个国家发展的境界。学校是传播文明的摇篮,是生长礼仪的沃土,是成就“礼仪之邦”的起点。那么,我们中学生又当如何去践行文明呢?我认为,第一、要语言文明。古语云:“诚于中而形于外”,文明礼貌是一个美好心灵的自然表露,语言文明是一个人整体形象的重要组成部分。语言文明,就是要让“请、你好、不好意思、谢谢、打扰了”成为自己的日常用语,就是要杜绝脏话,我们身边,还有一些同学出口成脏,对别人的心理造成了伤害,这就是不文明。在现实生活中,我们常会碰到这类情况:一句诚实、有礼貌的语言,可止息一场不愉快的争吵;一句粗野污秽的话,可导致一场轩然大波。

传统文化国旗下讲话:中华孝道文化的传承与创新
尊敬的各位领导,老师,亲爱的同学们:大家早上好!今天由我来为大家做国旗下的演讲,我演讲的主题是“中华孝道文化的传承与创新”。同学们应该对刚刚过去的清明节记忆犹新,也对即将到来的三月三歌圩节充满期待吧?可,是否有同学知道,这两个节日与中国孝道文化有着紧密的联系呢?清明节返乡祭祖表达了对已逝亲人的思念与尊敬;三月三歌圩节中的师公舞蕴含着浓浓的孝道文化,无一不在说明着中国传统与孝道文化的密不可分。孝道文化,即关爱父母长辈,尊老敬老的文化传统,是中国古代社会最基本的道德规范,也是中华民族尊奉的传统美德。它强调幼敬长,下尊上,要求晚辈尊敬老人,子女孝敬父母,爱护、照顾、赡养老人,使老人们颐养天年,享受天伦之乐。孝道文化经过千年的历史发展,已成为中华民族繁衍生息、代代相传的优良传统和核心价值观。孝敬是太阳,给人温暖;孝敬是大山,给人依靠;孝敬是水晶,是一笔宝贵的财富。俗话说,百善孝为先。古有晋人王祥卧冰求鲤,近有将军陈毅探望病母,古今中外孝的事例可谓数不胜数。俗话说,百善孝为先。从古至今,孝顺不仅是衡量个人道德水平高低的重要标准,也是社会秩序稳定运行的重要保障。然而在今天,有多少人又把这种传统的孝继承下来呢?是否社会在不断发展,人的物质生活水平不断提高,那么就可以对基本的孝的美德嗤之以鼻,置之一边呢?难道孝的故事永远只能停留在"感动中国"的历史中吗?这答案显然不是。孝道是我们每个人要秉持一生,永远的传承并发扬下去的。

文明伴我行国旗下讲话发言稿
做好文明礼仪要从生活中的点滴做起,从日常行为规范做起:一个微笑,一声问候,一句祝福,在你我之间传递;一个敬礼,一次礼让,一种搀扶,一点帮助在你我之间前行。着装得体、不求时尚;说话文明、举止大方;爱护公物、保护环境;尊重师长、学会关爱;遵守交通、不闯红灯;讲究卫生,不扔纸屑等等

2017吉林中考语文真题及答案
说时迟,那时快,薛霸的棍恰举起来,只见松树背后雷鸣也似一声,那条铁禅杖飞将来,把这水火棍一隔,丢去九霄云外,跳出一个胖大和尚来,喝道:“洒家在林子里听你多时!”……两个公人看那和尚时,穿一领皂布直裰,跨一口戒刀,提起禅杖,抡起来打两个公人。林冲刚才让开眼看时,认得是鲁智深。

2017北京市中考语文真题及答案
风能就是地球表面大量空气流动所产生的动能。据估算,全球风能约为2.74×1012千瓦,其中可利用的风能约为2×1010千瓦,比地球上可开发利用的水能总量要大10倍。 目前,风力发电已经成为风能利用的主要形式。随着经济的高速增长和能源消耗的持续上升,煤炭、石油等常规能源日益枯竭,环境持续恶化。

2014北京市中考语文真题及答案
余幼时即嗜学。家贫,无从致书以观,每假借于藏书之家,手自笔录,计日以还。天大寒,砚冰坚,手指不可屈伸,弗之怠。录毕,走送之,不敢稍逾约。以是人多以书假余,余因得遍观群书。

2020北京市中考语文真题及答案
十年春,齐师伐我。公将战,曹刿请见。其乡人日:“肉食者谋之,又何间焉?”刿曰:“肉食者鄙,未能远谋。”乃入见。问:“何以战?”公曰:“衣食所安,弗敢专也,必以分人。”

2015北京市中考语文真题及答案
【甲】予观夫巴陵胜状,在洞庭一湖。衔远山,吞长江,浩浩汤汤,横无际涯;朝晖夕阳,气象万千。此则岳阳楼之大观也,前人之述备矣。然则北通巫峡,南极潇湘,迁客骚人,多会于此,览物之情,得无异乎?
2016北京市中考语文真题及答案
京剧是流行全国的戏曲剧中之一。自清乾隆五十五年起,四大徽班陆续进京演出,他们相互影响,并接受昆区和秦腔的部分剧目、曲调、表演方法,又吸收了一些民间曲调,就是在这样的融合、演变和发展中京剧逐渐形成。在京剧发展的历程中,产生过许多优秀的演员。

