-

北师大初中数学八年级上册用计算器开方1教案
1.会用计算器求平方根和立方根;(重点)2.运用计算器探究数字规律,提高推理能力.一、情境导入前面我们通过平方和立方运算求出一些特殊数的平方根和立方根,如4的平方根是±2,116的平方根是±14,0.064的立方根是0.4,-8的立方根是-2等.那么如何求3,189,-39,311的值呢?二、合作探究探究点一:利用计算器进行开方运算 用计算器求6+7的值.解:按键顺序为■6+7=SD,显示结果为:9.449489743.方法总结:当被开方数不是一个数时,输入时一定要按键.解本题时常出现的错误是:■6+7=SD,错的原因是被开方数是6,而不是6与7的和,这样在输入时,对“6+7”进行开方,使得计算的是6+7而不是6+7,从而导致错误.K探究点二:利用科学计算器比较数的大小利用计算器,比较下列各组数的大小:(1)2,35;(2)5+12,15+2.解:(1)按键顺序:■2=SD,显示结果为1.414213562.按键顺序:SHIFT■5=,显示结果为1.709975947.所以2<35.

北师大初中数学九年级上册用频率估计概率1教案
(2)假如你摸一次,估计你摸到白球的概率P(白球)=;(3)试估算盒子里黑球有多少个.解:(1)0.6(2)0.6(3)设黑球有x个,则2424+x=0.6,解得x=16.经检验,x=16是方程的解且符合题意.所以盒子里有黑球16个.方法总结:本题主要考查用频率估计概率的方法,当摸球次数增多时,摸到白球的频率mn将会接近一个数值,则可把这个数值近似看作概率,知道了概率就能估算盒子里黑球有多少个.三、板书设计用频率估计概率用频率估计概率用替代物模拟试验估计概率通过实验,理解当实验次数较大时实验频率稳定于理论频率,并据此估计某一事件发生的概率.经历实验、统计等活动过程,进一步发展学生合作交流的意识和能力.通过动手实验和课堂交流,进一步培养学生收集、描述、分析数据的技能,提高数学交流水平,发展探索、合作的精神.
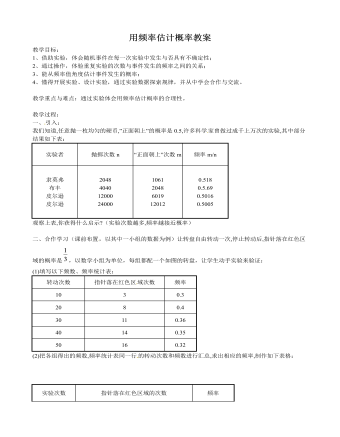
北师大初中数学九年级上册用频率估计概率2教案
(1)填写表格中次品的概率.(2)从这批西装中任选一套是次品的概率是多少?(3)若要销售这批西装2000件,为了方便购买次品西装的顾客前来调换,至少应该进多少件西装?六、课堂小结:尽管随机事件在每次实验中发生与否具有不确定性,但只要保持实验条件不变,那么这一事件出现的频率就会随着实验次数的增大而趋于稳定,这个稳定值就可以作为该事件发生概率的估计值。七、作业:课后练习补充:一个口袋中有12个白球和若干个黑球,在不允许将球倒出来数的前提下,小亮为估计口袋中黑球的个数,采用了如下的方法:每次先从口袋中摸出10个球,求出其中白球与10的比值,再把球放回袋中摇匀。不断重复上述过程5次,得到的白求数与10的比值分别为:0.4,0.1,0.2,0.1,0.2。根据上述数据,小亮可估计口袋中大约有 48 个黑球。

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

新人教版高中英语必修3Unit 1 Festivals and celebrations-Discovering Useful Structure教学设计
4.That was an experience that frightened everyone. →That was _____________________. 答案:1. taking 2. being discussed 3. in the reading room 4. a frightening experienceStep 6 The meaning and function of V-ing as the predicative动词-ing形式作表语,它通常位于系动词后面,用以说明主语“是什么”或“怎么样”一种表示主语的特质、特征和状态, 其作用相当于形容词; 另一种具体说明主语的内容, 即主语等同于表语, 两者可互换。The music they are playing sounds so exciting. 他们演奏的音乐听起来令人激动。The result is disappointing. 结果令人失望。Our job is playing all kinds of music. 我们的工作就是演奏各种音乐。Seeing is believing. 眼见为实。Step 7 Practice1. It is ________(amaze) that the boy is able to solve the problem so quickly.2. Buying a car is simply _______(waste) money. 3. Please stop making the noise—it’s getting ________(annoy). 4. complete the passage with the appropriate -ing form.La Tomatina is a festival that takes place in the Spanish town Bunol every August. I think many food festivals are __________ because people are just eating. however, this festival is _________ because people don't actually eat the tomatoes. Instead, they throw them at each other! the number of people ________ part in this tomato fight, can reach up to 20,000, and it is a very __________ fight that lasts for a whole hour. The _______ thing is how clean Bunol is after the tomatoes are washed away after the fight. this is because the juice form tomatoes is really good for making surfaces clean!答案:1. amazing 2. wasting 3. annoying4. boring interesting taking exciting amazing

新人教版高中英语必修3Unit 1 Festivals and Celebrations-Reading for Writing教学设计一
The topic of this part is “Write about your festival experience”.During the Listening and Speaking and Talking, students are just asked to say out their festival experiences such as the Spring Festival, Mid-autumn Day, but this part students will be asked to write down their own festival experiences. During the reading part, it introduces the Naadam Festival in Inner Mongolia Autonomous Region, which can give students a good example to imitate. Students not only learn the festival, but touch and feel the Inner Mongolian’s character, the spirit and cultural atmosphere, which can help students form the cultural awareness and learn to enjoy and value the diversity of Chinese culture.Concretely, the dairy tells the experience that the author spent the Naadam Festival in Inner Mongolia Autonomous Region with his/her friend. The structure is clear. In the opening paragraph, it introduces the topic of the Naadam Festival and the whole feeling. Then it introduces the items of the festival like the ceremony, wrestling and horse racing. Finally, it summarizes this experience. Because this part is a travel journal, we must guide students pay more attention to these details: 1. use the first person. 2. use the past tense to tell the past thing and use the present or future tense to describe the scenery. 3. use the timeline to tell the development. 4. be careful for the author’s psychology, emotion and feeling, etc.1. Read quickly to get main idea; read carefully to get the detailed information about Naadam Festival.2. Learn the structure of the reading article and language.3. Write an article about a festival experience4. Learn to use the psychology, emotions and feeling in the writing.1. Write an article about a festival experience.2. Use the structure of the reading article and language.

新人教版高中英语必修3Unit 2 Morals and Virtues-Reading and Thinking教学设计
The topic of this part is “Learn to make choices in life”.The Listening & Speaking & Talking part aims at the moral dilemmas, and this part is about making choices in life. The heroin is Lin Qiaozhi, a famous medical scientist, made a great contribution to our country’s medical care. Most importantly, her life experience can inspire our students whether in studying or the development of career. she had moral dilemmas and life choices, which are similar to the students who will step into society. Besides, Lin has quite good virtues like kindness, self-improvement, insistence, job-loving , generosity and responsibility, which is worth being learned.Concretely, this article is a biography about Lin Qiaozhi. The article tells her whole life according the timeline, among which the life choices is emphasized. For example, whether married or chased her dream, returned home or stayed abroad, family or public, her choices all reflected her faith, spirit, responsibility and devotion.1. Fast reading to get the detailed information about Lin Qiaozhi; careful reading to do the deductive information.2. Learn the reading skills--deductive judgement according the context.3. Study the structure features and language features. 4. Communicate about Lin’s life choices and reflect their own life choices.1. Learn the reading skills--deductive judgement according the context.2. Study the structure features and language features.3. Communicate about Lin’s life choices and reflect their own life choices.Step 1 Lead in---Small talkWhat are some important life choices?Importance choices: university study, jobs and marriage partners. Because they can determine our future.

新人教版高中英语必修3Unit 3 Diverse Cultures-Discovering Useful Structure教学设计
Step 4 PracticeRead the conversation. Find out which words have been left out.Justin: Linlin, I’m going to Guizhou Province next month. I’m super excited! Any recommendations for places to visit?Linlin: Wow, cool! Guizhou is a province with a lot of cultural diversity. Places to visit...well, definitely the Huangguoshu Waterfall first.Justin: What’s special about the waterfall?Linlin: Well, have you ever heard of the Chinese novel Journey to the West ?Justin: Yes, I have. Why ?Linlin: In the back of the waterfall, you will find a cave, which is the home of the Monkey King.Justin: Really? Cool! I’ll definitely check it out.Linlin:And I strongly recommend the ethnic minority villages. You’ll find Chinese culture is much more diverse than you thought.Justin:Sounds great, thanks.Answers:Justin: Linlin, I’m going to Guizhou Province next month. I’m super excited! Do you have any recommendations for places to visit?Linlin: Wow, that’s cool! Guizhou is a province with a lot of cultural diversity. What are some places to visit in Guizhou ? Well, definitely the Huangguoshu Waterfall is the first place to visit in Guizhou Province.Justin: What’s special about the waterfall?Linlin: Well, have you ever heard of the Chinese novel Journey to the West ?Justin: Yes, I have heard of the Chinese novel Journey to the West . Why do you ask if I have heard of the Chinese novel Journey to the West?Linlin: In the back of the waterfall, you will find a cave, which is the home of the Monkey King from Journey to the West.Justin: That’s really true? It’s Cool! I’ll definitely check it out.Linlin:And I strongly recommend the ethnic minority villages on your trip to Guizhou Province. You’ll find Chinese culture is much more diverse than you thought it was.Justin:This all sounds great, thanks.

新人教版高中英语必修3Unit 3 Diverse Cultures-Listening &Speaking&Talking教学设计
1. In Picture 1 and Picture 2, where do you think they are from? How do you know?From their wearings, we can know they are from ethnic minority of China--- Miao and Dong.Picture 1, they are playing their traditional instrument lusheng in their traditional costumes.Picture 2. the girls are Miao because they wear their traditional costumes and silver accessory.2. In Picture 3, can you find which village it is? What time is it in the picture?It is Dong village. It is at night. Step 2 While-listeningJustin met a new friend while traveling in Guizhou. Listen to their conversation and complete the summaries below.Part 1Justin and Wu Yue watched some Miao people play the lusheng. The instrument has a history of over 3,000 years and it is even mentioned in the oldest collection of Chinese poetry. Then they watched the lusheng dance. Justin wanted to buy some hand-made silver/traditional accessories as souvenirs. He was told that the price will depend on the percentage of silver. Part 2They will go to a pretty Dong minority village called Zhaoxing. they will see the drum towers and the wind and rain bridges. They may also see a performance of the Grand Song of the Dong people.Step 3 Post-listening---TalkingWork in groups. Imagine Justin is telling some friends about his trip to Guizhou. One of you is Justin and the rest of you are his friends. Ask Justin questions about his trip and experience. The following expressions may help you.

新人教版高中英语必修3Unit 4 Space Exploration-Listening&Speaking&Talking教学设计二
The themes of this part are “Talk about how to become an astronaut” and “Talk about life in space”. As Neil Armstrong said “Mystery creates wonder and wonder is the basis of man’s desire to understand. Space is difficult for human to reach, therefore, humans are full of wonders about it. However, if wanting to achieve the dream of reaching the Moon, some of our human should work hard to be an astronaut at first. Part A(Talk about how to become an astronaut) is a radio interview in a radio studio, where the host asked the Chinese astronauts about his story how to become an astronaut. Yang Liwei told his dreamed to be an astronaut since childhood. Then he worked hard to get into college at 22. The next 10 years, he gradually became an experienced pilot. At the same time, to be an astronaut, he had to study hard English, science and astronomy and trained hard to keep in good physical and mental health and to practise using space equipment. Part B (Talk about life in space) is also an interview with the astronaut Brown, who is back on the earth. The host Max asked about his space life, such as his emotion about going back the earth, the eating, shower, brushing, hobbies and his work. Part A and Part B are interviews. So expressing curiosity about the guests’ past life is a communicative skill, which students should be guided to learn.1. Students can get detailed information about how Yang Liwei became an astronaut and Max’s space life.2. Students learn to proper listening strategy to get detailed information---listening for numbers and taking notes.3. Students can learn related sentences or phrases to express their curiosity like “ I wish to know...” “I’d love to know...”4. Students can learn more about the space and astronauts, even be interested in working hard to be an astronaut

新人教版高中英语必修3Unit 4 Space Exploration-Reading for Writing教学设计二
⑦在我看来, 探索太空是值得的。As far as I am concerned, it is worthwhile to explore the space.Step 10 Writing---draftRecently, students in our class have had heated a discussion on whether space is worth exploring. Students hold different ideas about it.30% of us think space exploration is not worthwhile. They think space is too far away from us and our daily life and is a waste of money. And the money spent on space exploration can be used to solve the earth’s problems such as starvation and pollution.On the other hand,70% think space is worth exploring because we have benefited a lot from it,such as using satellites for communication and weather forecast. What’s more,with further space research,we may solve the population problem by moving to other planets one day. Also,space research will enable us to find new sources to solve the problem of energy shortages on the earth.As far as I am concerned, it is worthwhile to explore the space. Not only can it promote the development of society but also enrich our life. Step 11 Pair workExchange drafts with a partner. Use this checklist to help your partner revise his/her draft.1.Does the writer explain why he/she changed/wanted to change?2.Does the writer tell how the changes have improved or will improve his/her life?3.Is the text well-organised?4.Does the writer use words and expressions to show similarities and differences?5.Are there any grammar or spelling errors?6.Does the writer use correct punctuation?

新人教版高中英语必修3Unit 4 Space Exploration-Reading For Writing教学设计一
另一方面,其余的人反对这个计划,因为它可能会导致一些不好的影响。7.I hold the belief that space exploration not only enable us to understand how the universe began but also help us survived well into the future.我坚信探索太空不仅能够使我们了解宇宙的起源而且能够帮助我们更好地走进未来。8.I think we should spend more time and money exploring space so as to provide new and better solutions to people's shortterm and longterm problems.为了给人类的短期和长期问题提供更新和更好的解决方法,我认为我们应该花更多的时间和金钱来探索太空。9.From my point of view,it is wrong of young people to depend on their telephones too much,which may do harm to both their physical and mental health.在我看来,年轻人过度依赖手机是不对的,因为它们可能会对他们的身心健康都有害。最近你班同学就“人类是否应该进行宇宙探索”这个问题进行了激烈的讨论。有人认为,探索宇宙不仅让人类更好地了解宇宙的发展,还可以用来指导农业生产,以及把一些探索太空的高新技术用于现实生活;也有一些人认为探索太空花掉了大量的人力物力;影响了人们的生活水平。请你根据以下情况写一篇报告并发表自己的观点。注意:1.写作内容应包括以上全部要点,可适当发挥,使上下文连贯;

新人教版高中英语必修3Unit 5 The Value of Money-Listening &Speaking&Talking教学设计
4. A:We’d like to have someone to say a word at the beginning to welcome the group.B:↙Who?A:We thought that you or Dr.Johnson might do it.B用降调说Who,其意思是问,对方想让谁在开场时致欢迎词。Step 6 Pronunciation---Practice1. Listen to the short conversation and mark the intonation with ↗, ↙ or ↙, ↗. Then discuss with a partner what they intend to convey by using different intonation.Owner: You know what ?↗ It’s a million-pound bank note↙.Waiter 1: Really ?↗(question)Waiter 2: Really !↙(unbelievable and surprised)Waiter 3: Really ?!↙↗(first question then surprised)2. Listen to the conversations. Underline the parts that are stressed and mark the intonation. Then talk about the implied meanings of the responses with different intonations. Listen again and repeat.1) Henry: It’s a nice suit.Owner: Oh, it’s perfect!↙(The intonation means it is very suitable for Henry.)2) Henry: Well, that’s very kind of you.Owner: Kind, sir ?↗(what you said is not right) No, it’s kind of you. You must come whenever you want and have whatever you like. Just having you sit here is a great honour !!↙(welcome you to come again)3)Henry:Well, to be honest, I have none. Oliver:(happily) What luck!(excited) Brother↗, what luck!↙(It means “Didn’t you hear it?”)Henry: Well, it may seem lucky to you but not to me!↗(angry) If this is your idea of some kind of joke, I don’t think it’s very funny. Now if you’ll excuse me, I ought to be on my way.↙(If so, I would leave.)Roderick: Please don’t go↙...(hope Henry can wait for a moment)Part B Viewing and Talking---Describe people’s changing attitudes in a film clipStep 1 Before-listening---Tell the filmYou are going to watch part of the film The Million Pound Bank Note. Look at these photos and guess what happens in the film.

新人教版高中英语必修3Unit 5 The Value of Money-Listening &Speaking教学设计
Step 4: Listen again and decide if the following statements are true (T) or false (F).1 It was the first time Chen Liyan's story was reported. T口 F口2 Chen found 10,000 yuan in a small plastic bag in Taiyuan railway station口 F口3 Wang Zheng apologized to Chen because he couldn't offer her more money. T口 F口4 Chen took out a large loan to cure her daughter, T口 F口5 Wang set up a fundraising website for Chen's daughter after Chen told him about her situation. T口 F口Step 5:After listening, discuss the questions.1 What kind of person do you think Chen Liyan is?Chen Liyan is generous and honest because she returned a large sum of money to the owner.2 Did Chen return the money because she didn't need it?No. She returned the money because it was the right thing to do. Evidence for this is that she refused to accept the reward money because she felt that it had not been earned. 3 Is it common for people to do what Chen did?It depends on the culture. In some countries it is quite common to return money that has been found. In other countries, people believe "Finders are keepers!" 4 How did Wang Zheng feel about the return of his money?He must have been very happy and relieved to have gotten his money back. We know this because he thanked Chen repeatedly and even offered her a reward.5 Why did Ma Dongbao tell Wang about Chen's family?He must have had great sympathy for Chen and her daughter and wanted to help them.'We know this because he arranged help for them. 6 How did the news reporter feel about Chen's actions?The news reporter felt that it showed that money wasn't the most important thing in life. We know this because the reporter told us that this is what Chen believes. and then said, “that's a great attitude to take."

新人教版高中英语必修3Unit 5 The Value of Money-Reading and Thinking教学设计一
Everybody wants to get wealth.In today’s material world,making money or becoming wealthy symbolizes a person’s success and capability. Many people just make every effort, pay any price to attain greater wealth. With money,they can buy nice, large apartments in nice neighborhood. With money they can own luxurious cars. Wealth seems to bring all happiness in life.But is wealth the only road to happiness? Not really. There are many things in the world, which are beyond the means of money, such as friendship, love, health and knowledge. People are so preoccupied with struggling for money that they have no time or would not take the time to form or maintain friendship. What happiness can they feel living as lonely miserable creatures without love or friends in the world even if they accumulate tremendous wealth?In my opinion, people can’t do anything without money, but money is not everything. What money will bring you depends on your personal belief and goal in life. If you are kind enough to help others, especially the poor, money is a good thing to you. With it, you can do much more for the benefit of people and your country, and it will add to your own happiness. If you want money just for your own needs, you’ll never be satisfied or happy. In a word,you should have money spent for more people. Only then can money be the source of your happiness.Step 8 Homework4 students in a group, one acts Roderick, one Oliver, one servant and the fourth one acts Henry Adams, then listen to the tape, pay more attention to the difference between American English and British English in pronunciation, stress, tone.

新人教版高中英语必修3Unit 5 The Value of Money-Reading for Writing教学设计二
2. 您能看到, 我头发太长了。You can see that my hair is much too long.3. 无论什么时候, 只要您想回来就回来。Please come back whenever you want.4. 您仅有很少的头发要理! You only have too little hair to cut !5. 为您服务是我的荣幸!It is my honour to serve you!Step 9 Writing(Henry is walking down the street when he sees a sign for a place that cuts hair. He decides to have it cut. )H=Henry B=BarberH: Good afternoon, I’d like to have my hair cut, if I may. (The barber looks at Henry’s hair and continues cutting another man’s hair. ) Er, I’d really like a haircut. As you can see it’s much too long. B: (in a rude manner) Yes, I can see that. Indeed, I can. H: Fine, well, I’ll have a seat then. (He sits in one of the barber’s chairs. The barber turns to look at Henry. )B: It’s quite expensive here, you know! Are you sure you can afford it?H: Yes. I think so. (After his hair is cut, the barber tells Henry how much he must pay. Henry shows the barber the bank note. )B: Why Mr. . . (looks shocked)H: Adams. Henry Adams. I’m sorry. I don’t have any change. B: Please don’t worry! (wearing a big smile) Nothing to worry about! Nothing at all! Please come back whenever you want, even if you only have too little hair to cut! It will be my honour to serve you!Step 10 Pair workExchange drafts with a partner. Use this checklist to help your partner revise his/her draft.1. Are all the elements of a play included and in good order ?2. Do the character use suitable language ?3. Are the stage directions clear and useful ?4. Is the plot clear and exciting enough ?

新人教版高中英语选修2Unit 4 Journey Across a Vast Land教学设计
当孩子们由父母陪同时,他们才被允许进入这个运动场。3.过去分词(短语)作状语时的几种特殊情况(1)过去分词(短语)在句中作时间、条件、原因、让步状语时,相当于对应的时间、条件、原因及让步状语从句。Seen from the top of the mountain (=When it is seen from the top of the mountain), the whole town looks more beautiful.从山顶上看,整个城市看起来更美了。Given ten more minutes (=If we are given ten more minutes), we will finish the work perfectly.如果多给十分钟,我们会完美地完成这项工作。Greatly touched by his words (=Because she was greatly touched by his words), she was full of tears.由于被他的话深深地感动,她满眼泪花。Warned of the storm (=Though they were warned of the storm), the farmers were still working on the farm.尽管被警告了风暴的到来,但农民们仍在农场干活。(2)过去分词(短语)在句中作伴随、方式等状语时,可改为句子的并列谓语或改为并列分句。The teacher came into the room, followed by two students (=and was followed by two students).后面跟着两个学生,老师走进了房间。He spent the whole afternoon, accompanied by his mom(=and was accompanied by his mom).他由母亲陪着度过了一整个下午。

新人教版高中英语选修2Unit 1 Science and Scientists-Reading and thinking教学设计
Step 5: After learning the text, discuss with your peers about the following questions:1.John Snow believed Idea 2 was right. How did he finally prove it?2. Do you think John Snow would have solved this problem without the map?3. Cholera is a 19th century disease. What disease do you think is similar to cholera today?SARS and Covid-19 because they are both deadly and fatally infectious, have an unknown cause and need serious public health care to solve them urgently.keys:1. John Snow finally proved his idea because he found an outbreak that was clearly related to cholera, collected information and was able to tie cases outside the area to the polluted water.2. No. The map helped John Snow organize his ideas. He was able to identify those households that had had many deaths and check their water-drinking habits. He identified those houses that had had no deaths and surveyed their drinking habits. The evidence clearly pointed to the polluted water being the cause.3. SARS and Covid-19 because they are both deadly and fatally infectious, have an unknown cause and need serious public health care to solve them urgently.Step 6: Consolidate what you have learned by filling in the blanks:John Snow was a well-known _1___ in London in the _2__ century. He wanted to find the _3_____ of cholera in order to help people ___4_____ it. In 1854 when a cholera __5__ London, he began to gather information. He ___6__ on a map ___7___ all the dead people had lived and he found that many people who had ___8____ (drink) the dirty water from the __9____ died. So he decided that the polluted water ___10____ cholera. He suggested that the ___11__ of all water supplies should be _12______ and new methods of dealing with ____13___ water be found. Finally, “King Cholera” was __14_____.Keys: 1. doctor 2. 19th 3.cause 4.infected with 5.hit 6.marked 7.where 8.drunk 9.pump 10.carried 11.source 12.examined 13.polluted 14.defeatedHomework: Retell the text after class and preview its language points

新人教版高中英语选修2Unit 1 Science and Scientists-Using langauge教学设计
This happens because the dish soap molecules have a strong negative charge, and the milk molecules have a strong positive charge. Like magnets, these molecules are attracted to each other, and so they appear to move around on the plate, taking the food coloring with them, making it look like the colors are quickly moving to escape from the soap.Listening text:? Judy: Oh, I'm so sorry that you were ill and couldn't come with us on our field trip. How are you feeling now? Better?? Bill: Much better, thanks. But how was it?? Judy: Wonderful! I especially liked an area of the museum called Light Games.it was really cool. They had a hall of mirrors where I could see myself reflected thousands of times!? Bill: A hall of mirrors can be a lot of fun. What else did they have?? Judy: Well, they had an experiment where we looked at a blue screen for a while, and then suddenly we could see tiny bright lights moving around on it. You'll never guess what those bright lights were!? Bill: Come on, tell me!? Judy: They were our own blood cells. For some reason, our eyes play tricks on us when we look at a blue screen, and we can see our own blood cells moving around like little lights! But there was another thing I liked better. I stood in front of a white light, and it cast different shadows of me in every color of the rainbow!? Bill: Oh, I wish I had been there. Tell me more!? Judy: Well, they had another area for sound. They had a giant piano keyboard that you could use your feet to play. But then, instead of playing the sounds of a piano, it played the voices of classical singers! Then they had a giant dish, and when you spoke into it, it reflected the sound back and made it louder. You could use it to speak in a whisper to someone 17 meters away.? Bill: It all sounds so cool. I wish I could have gone with you? Judy: I know, but we can go together this weekend. I'd love to go there again!? Bill: That sounds like a great idea!

新人教版高中英语选修2Unit 2 Bridging Cultures-Discovering useful structures教学设计
The grammar of this unit is designed to review noun clauses. Sentences that use nouns in a sentence are called noun clauses. Nominal clauses can act as subject, object, predicate, appositive and other components in compound sentences. According to the above-mentioned different grammatical functions, nominal clauses are divided into subject clause, object clause, predicate clause and appositive clause. In this unit, we will review the three kinds of nominal clauses. Appositive clauses are not required to be mastered in the optional compulsory stage, so they are not involved.1. Guide the students to judge the compound sentences and determine the composition of the clauses in the sentence.2. Instruct students to try to learn grammar by generalizing grammar rules, controlling written practice, and semi-open oral output.3. Inspire the students to systematize the function and usage of noun clause1.Instruct students to try to learn grammar by generalizing grammar rules, controlling written practice, and semi-open oral output.2.Inspire the students to systematize the function and usage of noun clauseStep1: The teacher ask studetns to find out more nominal clauses from the reading passage and udnerline the nominal clauses.





















