-
人教A版高中数学必修二事件的相互独立性教学设计
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
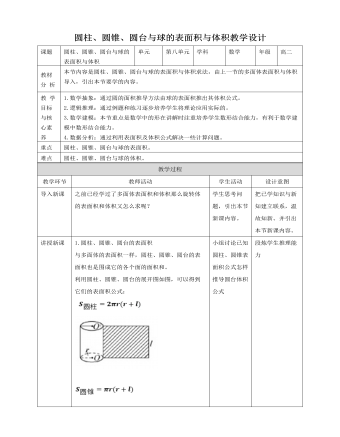
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。

人教版高中历史必修3物理学的重大进展说课稿2篇
二、相对论的创立【课件】展示下列材料艾伯特·爱因斯坦(1879——1955),1879年3月14日诞生在德国乌尔姆的一个犹太人家中。1894年举家迁居意大利米兰。1900年毕业于瑞士苏黎世工业大学。爱因斯坦被认为是最富于创造力的科学家,他不但创立了相对论,还提出了光量子的概念,得出了光电效应的基本定律,并揭示了光的波粒二重性本质,为量子力学的建立奠定基础。为此荣获1921年度的诺贝尔物理学奖。同时,他还证明了热的分子运动论,提出了测定分子大小的新方法。【问题】19世纪末20世纪初爱因斯坦对物理学的贡献是什么?意义是什么?为什么会出现?1、背景:经典物理学的危机。19世纪末三大发现:x射线、放射性和电子,经典力学无法解释研究中的新问题,如:黑体辐射、光电效应等。2、相对论的提出及主要内容:(1)“狭义相对论”和光速不变原理:1905年提出。

小学美术桂美版一年级上册《第10课神奇的果树》教学设计说课稿
2学情分析 新入学的学生第一次接触正规化的美术课,对一年级学生来说是新 奇、有趣、好玩的,而且新生入学前所受的教育各不相同,心理因素 也不一样,在绘画上、工艺制作上一定有着自己的创造思维、想象能 力和自己的个性,但这些会造成学习的不一致性、习惯不统一化,给 美术课的课堂带来不必要的麻烦。因此, 对待这些刚进入课堂的小朋友, 我们在情感态度上要做出很大 的努力,小学生在思维的想象力、创造力方面发展的空间很大,所以 我们要好好把握机会, 激发孩子们对美术学习的兴趣,让孩子们能发 现美,有创造美的想法。

小学美术桂美版三年级上册《第10课漂亮的纸袋》教学设计说课稿
一.激趣导入。 1. 教师展示做好的漂亮纸袋,让孩子们产生想要动手的愿望。 2.结合多媒体课件,出示漂亮纸袋。 同学们,这些袋子漂亮吗?你喜欢吗?发现这些纸袋都是什么做成的?下面我们就来做一做这些漂亮的纸袋。 二.学习制作纸袋的基本过程。 1.教师出示制作纸袋需要准备好的东西,让孩子们自主检查是否准备齐全。 2.多媒体出示纸袋制作步骤,让学生注意观察,清晰每一步制作的过程: (1)把长方形的对折,画上虚线,用小剪刀剪去我们不需要的部分,然后用双面胶粘贴,形成一个纸袋。

小学美术桂美版一年级上册《第4课动物的花衣裳》教学设计说课稿
2学情分析 1、这一课是一年级的“造型·表现”学习领域,一年级孩子自制力较差,注意力集中时间不长,缺乏一定的造型能力,但好奇心很强,表现欲望非常强烈,非常希望得到老师和同学们的认可,从他们的兴趣入手就能达到事半功倍的效果;2、教学方式应该是直观的;3、让学生通过欣赏与想象进行创作,激发他们对大自然的兴趣,感受大自然的美。

小学美术桂美版一年级上册《第6课送给老师的爱》教学设计说课稿
教学过程:一、组织教学,导入学习1.观察导入,激发兴趣(教具出示)2.教师和学生一起做猜节日的游戏,激发学生的兴趣。 每年的9月10日都是教师们最开心的日子,也是学生们表达对老师尊敬的日子,中国自古以来便有尊师重教的传统,《教师法》 第四条规定全社会应当尊重教师。

小学美术桂美版三年级上册《第15课实用美观的竹器》教学设计说课稿
2学情分析本课内容选用了苗族阿姐的背篓,黎族阿爸的鱼笼,竹摇篮、簸箕等借助家庭中常见的竹器作为学习内容,目的是要求学生用线描的方法对竹器的外形及竹编的篾纹进行描绘,锻炼学生对事物的观察能力和表现能力。在此之前学生已经学过了如何用线描的方式描绘生活中的小物件,这为过渡到本课内容的学习起到了铺垫作用,同时为后面的素描教学内容打下造型基础。

小学美术桂美版一年级上册《第1课美丽的大自然》教学设计说课稿
教学目标 知识目标:通过欣赏大自然的图片,感知大自然不同特点的美。 技能目标:能用自己喜欢的方式表达对不同自然美的感受。 情感态度与价值观:培养学生热爱大自然的情感,及爱护大自然的情感。 教学重点让学生感受大自然不同的美,了解大自然的丰富,并能用简单的语言表达自己的感受。 教学难点学习用审美的眼光去观察大自然。 主要教法启发引导法、自学尝试法 学习指导体验探究法辅助指导法 教学资源教师:教材、课件。 学生:教材、自然风光片 教学过程: 教学活动教学意图 教师学生

小学科学鄂教版三年级下册《凤仙花的一生》说课稿
二、教学目标 ★知识与技能目标: 1、能正确指认绿色开花植物的六大器官; 2、能说出绿色开花植物的相同点和不同点; 3、能用图画或文字描述并记录所观察的植物。 ★过程与方法: 学生在自主探究解决问题的过程中获取认识新知的方法。 ★情感态度与价值观: 在进行探究活动的过程中激发学生研究植物的兴趣,培养学生的合作意识和创新精神。 三、教学重难点 重点:认识绿色开花植物的六大器官。 难点:能用图画或文字描述并记录所观察的植物。

大班体育综合训练活动“可爱的小青蛙”课件教案
2、让幼儿在活动中体验合作的乐趣,培养他们解决问题、克服困难的好品质,激发幼儿的团队精神。活动准备:竹筐20个(边筐高25厘米)、4张圆形大小不一的荷叶、纸皮(荷叶)每人一张活动过程:一、准备活动1、 音乐游戏“小青蛙醒来了”。教师与幼儿随着音乐做各种动作,活动身体。2、 幼儿每人选一张“荷叶”,摆在地上,进行跳进跳出动作练习,(教师提醒幼儿注意起跳时先屈膝,落地要轻)

“全国中小学生安全教育日”国旗下讲话稿:我的安全我能行
尊敬的老师、亲爱的同学们:大家早上好!大家知道今天是什么日子吗?今天是第20个“全国中小学生安全教育日“。从1996年起,我们国家确定每年3月份最后一周的星期一为“全国中小学生安全教育日”。今年的安全教育主题是“我安全、我健康、我快乐”。这一周也是第8个“福建省学校安全教育周“。今天我国旗下讲话的题目就是“我的安全我能行”。校园是人员密集的场所,校园安全关系到每个家庭的幸福。因此,创建平安校园是每一名老师和同学的共同心愿。大家还记得,XX年9月26日下午,昆明市北京路明通小学发生一起踩踏事故,造成学生6人死亡、26人受伤。事情的起因是头一天下午,该小学体育老师将两块体育教学使用的海绵垫子临时靠墙放置于学生午休宿舍楼一楼单元过道处。26日14时许,学校起床铃拉响后,该小学一、二年级午休学生起床后返回教室上课,由于靠墙的一块海绵垫平倒于一楼过道,造成通道不畅,先期下楼的学生在通过海绵垫时发生跌倒,后续下楼的大量学生不清楚情况,继续向前拥挤造成相互叠加挤压,导致严重伤亡。专家研究和实践证明:通过安全教育,强化安全管理,提高广大师生的自我保护能力,80%的意外伤害是完全可以避免的。

人教版高中政治必修1科学发展观和小康社会的经济建设说课稿
一、对教材分析1、地位和作用课程标准对本课的基本要求是:阐明科学发展观的涵义和说明全面建设小康社会的经济目标,最根本的是以经济建设为中心,不断解放和发展社会生产力。这一课在新教材中有着重要地位,且对我们的经济生活具有深远的指导意义和教育意义。同时对学生树立科学发展观有着重要的导向作用,对学生树立共同理想和远大理想有着重大的影响作用。因此,本课书是新教材的教育目的和归宿。2、教学目标(1)知识目标:了解总体小康水平的特征和全面建设小康社会的要求;理解科学发展观的科学内涵;运用促进国民经济又好又快发展的措施的基本要求。(2)能力目标 :能准确把握科学发展观科学内涵的理解能力;可以运用所学知识解决现实问题、参与经济生活的能力。(3)情感、态度与价值观目标:通过总体小康社会的建设增强民族自豪感;牢固树立科学发展观;增强节约意识;增强参与经济生活的自觉性。

抛物线的简单几何性质(2)教学设计人教A版高中数学选择性必修第一册
二、直线与抛物线的位置关系设直线l:y=kx+m,抛物线:y2=2px(p>0),将直线方程与抛物线方程联立整理成关于x的方程k2x2+2(km-p)x+m2=0.(1)若k≠0,当Δ>0时,直线与抛物线相交,有两个交点;当Δ=0时,直线与抛物线相切,有一个切点;当Δ<0时,直线与抛物线相离,没有公共点.(2)若k=0,直线与抛物线有一个交点,此时直线平行于抛物线的对称轴或与对称轴重合.因此直线与抛物线有一个公共点是直线与抛物线相切的必要不充分条件.二、典例解析例5.过抛物线焦点F的直线交抛物线于A、B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴.【分析】设抛物线的标准方程为:y2=2px(p>0).设A(x1,y1),B(x2,y2).直线OA的方程为: = = ,可得yD= .设直线AB的方程为:my=x﹣ ,与抛物线的方程联立化为y2﹣2pm﹣p2=0,

椭圆的简单几何性质(2)教学设计人教A版高中数学选择性必修第一册
二、典例解析例5. 如图,一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口 ABC是椭圆的一部分,灯丝位于椭圆的一个焦点F_1上,片门位另一个焦点F_2上,由椭圆一个焦点F_1 发出的光线,经过旋转椭圆面反射后集中到另一个椭圆焦点F_2,已知 〖BC⊥F_1 F〗_2,|F_1 B|=2.8cm, |F_1 F_2 |=4.5cm,试建立适当的平面直角坐标系,求截口ABC所在的椭圆方程(精确到0.1cm)典例解析解:建立如图所示的平面直角坐标系,设所求椭圆方程为x^2/a^2 +y^2/b^2 =1 (a>b>0) 在Rt ΔBF_1 F_2中,|F_2 B|= √(|F_1 B|^2+|F_1 F_2 |^2 )=√(〖2.8〗^2 〖+4.5〗^2 ) 有椭圆的性质 , |F_1 B|+|F_2 B|=2 a, 所以a=1/2(|F_1 B|+|F_2 B|)=1/2(2.8+√(〖2.8〗^2 〖+4.5〗^2 )) ≈4.1b= √(a^2 〖-c〗^2 ) ≈3.4所以所求椭圆方程为x^2/〖4.1〗^2 +y^2/〖3.4〗^2 =1 利用椭圆的几何性质求标准方程的思路1.利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是:(1)确定焦点位置;(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程);(3)根据已知条件构造关于参数的关系式,利用方程(组)求参数,列方程(组)时常用的关系式有b2=a2-c2等.

用空间向量研究直线、平面的位置关系(2)教学设计人教A版高中数学选择性必修第一册
跟踪训练1在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC;(2)BD1⊥EB1.(2)∵(BD_1 ) ?=(-1,-1,1),(EB_1 ) ?=(1/2 "," 1/2 "," 1),∴(BD_1 ) ?·(EB_1 ) ?=(-1)×1/2+(-1)×1/2+1×1=0,∴(BD_1 ) ?⊥(EB_1 ) ?,∴BD1⊥EB1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E(1/2 "," 1/2 "," 0),B1(1,1,1).(1)∵(BD_1 ) ?=(-1,-1,1),(AC) ?=(-1,1,0),∴(BD_1 ) ?·(AC) ?=(-1)×(-1)+(-1)×1+1×0=0.∴(BD_1 ) ?⊥(AC) ?,∴BD1⊥AC.例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.思路分析一种思路是不建系,利用基向量法证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直,从而根据线面垂直的判定定理证得结论;另一种思路是建立空间直角坐标系,通过坐标运算证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直;还可以在建系的前提下,求得平面EFB1的法向量,然后说明(D_1 M) ?与法向量共线,从而证得结论.证明:(方法1)因为E,F,M分别为棱AB,BC,B1B的中点,所以(D_1 M) ?=(D_1 B_1 ) ?+(B_1 M) ?=(DA) ?+(DC) ?+1/2 (B_1 B) ?,而(B_1 E) ?=(B_1 B) ?+(BE) ?=(B_1 B) ?-1/2 (DC) ?,于是(D_1 M) ?·(B_1 E) ?=((DA) ?+(DC) ?+1/2 (B_1 B) ?)·((B_1 B) ?-1/2 (DC) ?)=0-0+0-1/2+1/2-1/4×0=0,因此(D_1 M) ?⊥(B_1 E) ?.同理(D_1 M) ?⊥(B_1 F) ?,又因为(B_1 E) ?,(B_1 F) ?不共线,因此D1M⊥平面EFB1.

双曲线的简单几何性质(2)教学设计人教A版高中数学选择性必修第一册
二、典例解析例4.如图,双曲线型冷却塔的外形,是双曲线的一部分,已知塔的总高度为137.5m,塔顶直径为90m,塔的最小直径(喉部直径)为60m,喉部标高112.5m,试建立适当的坐标系,求出此双曲线的标准方程(精确到1m)解:设双曲线的标准方程为 ,如图所示:为喉部直径,故 ,故双曲线方程为 .而 的横坐标为塔顶直径的一半即 ,其纵坐标为塔的总高度与喉部标高的差即 ,故 ,故 ,所以 ,故双曲线方程为 .例5.已知点 到定点 的距离和它到定直线l: 的距离的比是 ,则点 的轨迹方程为?解:设点 ,由题知, ,即 .整理得: .请你将例5与椭圆一节中的例6比较,你有什么发现?例6、 过双曲线 的右焦点F2,倾斜角为30度的直线交双曲线于A,B两点,求|AB|.分析:求弦长问题有两种方法:法一:如果交点坐标易求,可直接用两点间距离公式代入求弦长;法二:但有时为了简化计算,常设而不求,运用韦达定理来处理.解:由双曲线的方程得,两焦点分别为F1(-3,0),F2(3,0).因为直线AB的倾斜角是30°,且直线经过右焦点F2,所以,直线AB的方程为

人教版高中语文必修3《一名物理学家的教育历程》教案
①阐发话题式:就是用简练的语言对所给话题材料加以概括和浓缩,并找到一个最佳切入点加以深层次阐述。吉林一考生的满分作文《漫谈“感情”“认知”》的题记是:“同是对‘修墙’‘防盗’的预见,却产生‘聪明’或‘被怀疑’的结果。‘感情’竟能如此地左右着‘认知’,心的小舟啊,在文化的河流中求索。”这个题记通过对材料的简单解释,将“感情”与“认知”二者的关系诠释得非常明白,也点明了作者的态度和议论的中心。②诠释题目式:所拟题目一般都具有深刻性特点,运用题记形式对题目进行巧妙而又全面的诠释。云南一考生的满分作文《与你同行》的题记是:“他们一路同行,一个汲着水,一个负着火,形影相随。在他们携手共进时,就产生了智慧。”这个题记形象而深刻地对“与你同行”这个题目进行了解释,言简意赅,表明了考生对感情和理智关系的认识。

人教A版高中数学必修一两角和与差的正弦、余弦和正切公式教学设计(2)
本节内容是三角恒等变形的基础,是正弦线、余弦线和诱导公式等知识的延伸,同时,它又是两角和、差、倍、半角等公式的“源头”。两角和与差的正弦、余弦、正切是本章的重要内容,对于三角变换、三角恒等式的证明和三角函数式的化简、求值等三角问题的解决有着重要的支撑作用。 课程目标1、能够推导出两角和与差的正弦、余弦、正切公式并能应用; 2、掌握二倍角公式及变形公式,能灵活运用二倍角公式解决有关的化简、求值、证明问题.数学学科素养1.数学抽象:两角和与差的正弦、余弦和正切公式; 2.逻辑推理: 运用公式解决基本三角函数式的化简、证明等问题;3.数学运算:运用公式解决基本三角函数式求值问题.4.数学建模:学生体会到一般与特殊,换元等数学思想在三角恒等变换中的作用。.

