-

人教版高中地理选修2长江三峡工程建设的意义和作用教案
1、图5.3“长江中游防洪形势图”(1)读图后,说出长江中游的主要水文特征:多曲流、多支流、多湖泊。(2)分析“千里长江,险在荆江”的原因及其解决的措施:荆江河段特别弯曲,有“九曲回肠”之称,水流不畅,泥沙大量淤积,使河床高出两岸平地,形成“悬河”。一旦发生洪水,堤防漫溃直接威胁江汉平原和洞庭湖区的农田、企业、城市、交通要道和人民生命财产安全。新中国成立后,治理荆江的措施主要有:修建荆江分洪工程,完成了几处裁弯取直工程,加固了荆江大堤。(3)在图上找出主要分洪区。2、图5.5“长江三峡图”(1)掌握长江三峡的组成、名称及其在图上的位置:说明:①长江三峡的长度数据有多种,如192千米、193千米、204千米208千米等。②有的著作中把大宁河宽谷划入瞿塘峡,把香溪宽谷划入西陵峡。

人教版新课标高中物理必修1时间和位移教案2篇
一、教学目标1、知识与技能(1)知道时间和时刻的含义以及它们的区别。知道在实验室测量时间的方法。(2)知道位移的概念,知道它是表示质点位置变动的物理量,知道它是矢量,可以用有向线段来表示。(3)知道位移和路程的区别。2、过程与方法(1)联系生活实际,通过师生共同讨论的方法来确定时刻与时间、位置、位移及其路程的关系。(2)通过类比的数学方法用数学上的点、线段来突破时刻与时间的关系,直线运动的位置和位移。(3)尝试运用所学的概念判断一些与生活相关的实际问题。3.情感态度与价值观(1)通过本节课的学习,使学生体会到物理现象和规律所蕴含的自然美。(2)通过对问题的讨论,培养学生勇于探究与日常生活有关的物理学问题。(3)培养学生有主动与他人合作的团队精神,提高学生的科学素养。二、教学重点、难点重点:1、时间、时刻、位置、位移的概念。2、矢量与标量的概念。

人教版新课标高中物理必修1质点参考系和坐标系教案2篇
①平动的物体一般可以看作质点做平动的物体,由于物体上各点的运动情况相同,可以用一个点代表整个物体的运动,在这种情况下,物体的大小、形状就无关紧要了,可以把整个物体当质点。例如:平直公路上行驶的汽车,车身上各部分的运动情况相同,当我们把汽车作为一个整体来研究它的运动的时候,就可以把汽车当作质点。当然,假如我们需要研究汽车轮胎的运动,由于轮胎上各部分运动情况不相同,那就不能把它看作质点了。要注意的是:同一物体在不同情况下有时可看质点,有时不可以看作质点,一列火车从北京开到上海,研究火车的运行的时间,可将火车看成质点,而火车过桥时,计算火车过桥的时间,不可以将火车看成质点。②有转动但转动为次要因素例如:研究地球公转时,可把地球看作质点;研究地球自转时,不能把地球看作质点。③物体的形状、大小可忽略再如:乒乓球旋转对球的运动的较大的影响,运动员在发球、击球时都要考虑,就不能把乒乓球简单看作质点。

人教版新课标高中物理必修1时间和位移教案2篇
2、过程与方法(1)联系生活实际,通过师生共同讨论的方法来确定时刻与时间、位置、位移及其路程的关系。(2)通过类比的数学方法用数学上的点、线段来突破时刻与时间的关系,直线运动的位置和位移。(3)尝试运用所学的概念判断一些与生活相关的实际问题。3.情感态度与价值观(1)通过本节课的学习,使学生体会到物理现象和规律所蕴含的自然美。(2)通过对问题的讨论,培养学生勇于探究与日常生活有关的物理学问题。(3)培养学生有主动与他人合作的团队精神,提高学生的科学素养。二、教学重点、难点重点:1、时间、时刻、位置、位移的概念。2、矢量与标量的概念。难点:1、时刻与时间、路程和位移的区别。2、用坐标表示时刻、时间、位移的方法。3、矢量与标量的区别。

人教版新课标高中物理必修1质点参考系和坐标系教案2篇
(创设实例:多媒体播放视频刘翔的110m栏。)1.提出问题:怎样定量(准确)人描述车或刘翔所在的位置?2.提示:你的描述必须能反映物体(或人)的运动特点(直线)、运动方向、各点之间的距离等因素。3.总结:①为了定量地描述物体的位置及位置的变化,需要在参考系上建立适当的坐标系。坐标系是在参考系的基础上抽象出来的概念,是抽象化的参考系。为了定量地描述物体的位置及位置的变化需要在参考系上建立适当的坐标系,如果物体在一维空间运动,即沿一条直线运动,只需建立直线坐标系,就能准确表达物体的位置;如果物体在二维空间运动,即在同一平面运动,就需要建立平面直角坐标系来描述物体的位置;当物体在三维空间运动时,则需要建立三维坐标系。①一维坐标:描述物体在一条直线上运动,即物体做一维运动时,可以以这条直线为x轴,在直线上规定原点、正方向和单位长度,建立直线坐标系。如图1-1-1所示,若某一物体运动到A点,此时它的位置坐标XA=3m,若它运动到B点,则此时它的坐标XB=-2m(“-”表示沿X轴负方向)。

人教版新课标高中物理必修2动能和动能定理教案2篇
二、课堂教学(课前由科代表发回预习学案)1、教师根据预习学案检查结果提出问题(用多媒体展示),引导全班讨论(重点讨论:①、为什么动能的表达式一定是 mV2 ?你如何得出这个结论?②、力在一个过程中对物体所做的功,和物体在这个过程中动能的变化量有什么关系?你如何得出这个结论?这个做功的力和F=ma中的力F有什么关系)。有困难的小组应及时问老师。老师在这个过程中巡视指导。2、学生自主阅读课文“7 动能和动能定理”中的“动能的表达式”,然后完成如下练习(教师在此过程中巡视指导):2.1尝试推出动能的表达式(鼓励会推导的同学积极上台板演,老师引导讨论)。2.2写出动能的小结(认真阅读教材p66倒数第二段、第三段,结合你推导动能表达式的过程,认真思考后四人一组讨论:①、动能是矢量还是标量?②、动能的单位是什么?③、你认为应从哪几方面来理解动能?)

人教A版高中数学必修一对数函数的图像和性质教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.2节《对数函数的图像和性质》 是高中数学在指数函数之后的重要初等函数之一。对数函数与指数函数联系密切,无论是研究的思想方法方法还是图像及性质,都有其共通之处。相较于指数函数,对数函数的图象亦有其独特的美感。在类比推理的过程中,感受图像的变化,认识变化的规律,这是提高学生直观想象能力的一个重要的过程。为之后学习数学提供了更多角度的分析方法。培养和发展学生逻辑推理、数学直观、数学抽象、和数学建模的核心素养。1、掌握对数函数的图像和性质;能利用对数函数的图像与性质来解决简单问题;2、经过探究对数函数的图像和性质,对数函数与指数函数图像之间的联系,对数函数内部的的联系。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;渗透类比等基本数学思想方法。
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
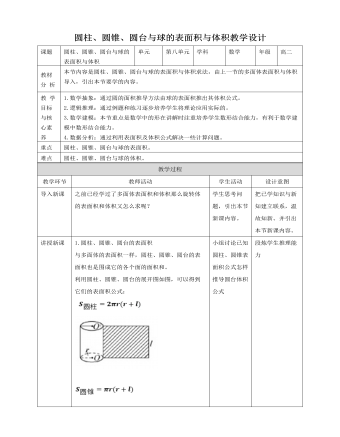
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.

人教版高中数学选择性必修二等差数列的前n项和公式(1)教学设计
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献. 问题1:为什么1+100=2+99=…=50+51呢?这是巧合吗?试从数列角度给出解释.高斯的算法:(1+100)+(2+99)+…+(50+51)= 101×50=5050高斯的算法实际上解决了求等差数列:1,2,3,…,n,"… " 前100项的和问题.等差数列中,下标和相等的两项和相等.设 an=n,则 a1=1,a2=2,a3=3,…如果数列{an} 是等差数列,p,q,s,t∈N*,且 p+q=s+t,则 ap+aq=as+at 可得:a_1+a_100=a_2+a_99=?=a_50+a_51问题2: 你能用上述方法计算1+2+3+… +101吗?问题3: 你能计算1+2+3+… +n吗?需要对项数的奇偶进行分类讨论.当n为偶数时, S_n=(1+n)+[(2+(n-1)]+?+[(n/2+(n/2-1)]=(1+n)+(1+n)…+(1+n)=n/2 (1+n) =(n(1+n))/2当n为奇数数时, n-1为偶数

人教版高中数学选择性必修二等比数列的前n项和公式 (1) 教学设计
新知探究国际象棋起源于古代印度.相传国王要奖赏国际象棋的发明者,问他想要什么.发明者说:“请在棋盘的第1个格子里放上1颗麦粒,第2个格子里放上2颗麦粒,第3个格子里放上4颗麦粒,依次类推,每个格子里放的麦粒都是前一个格子里放的麦粒数的2倍,直到第64个格子.请给我足够的麦粒以实现上述要求.”国王觉得这个要求不高,就欣然同意了.假定千粒麦粒的质量为40克,据查,2016--2017年度世界年度小麦产量约为7.5亿吨,根据以上数据,判断国王是否能实现他的诺言.问题1:每个格子里放的麦粒数可以构成一个数列,请判断分析这个数列是否是等比数列?并写出这个等比数列的通项公式.是等比数列,首项是1,公比是2,共64项. 通项公式为〖a_n=2〗^(n-1)问题2:请将发明者的要求表述成数学问题.

人教版高中数学选择性必修二等比数列的前n项和公式 (2) 教学设计
二、典例解析例10. 如图,正方形ABCD 的边长为5cm ,取正方形ABCD 各边的中点E,F,G,H, 作第2个正方形 EFGH,然后再取正方形EFGH各边的中点I,J,K,L,作第3个正方形IJKL ,依此方法一直继续下去. (1) 求从正方形ABCD 开始,连续10个正方形的面积之和;(2) 如果这个作图过程可以一直继续下去,那么所有这些正方形的面积之和将趋近于多少?分析:可以利用数列表示各正方形的面积,根据条件可知,这是一个等比数列。解:设正方形的面积为a_1,后续各正方形的面积依次为a_2, a_(3, ) 〖…,a〗_n,…,则a_1=25,由于第k+1个正方形的顶点分别是第k个正方形各边的中点,所以a_(k+1)=〖1/2 a〗_k,因此{a_n},是以25为首项,1/2为公比的等比数列.设{a_n}的前项和为S_n(1)S_10=(25×[1-(1/2)^10 ] )/("1 " -1/2)=50×[1-(1/2)^10 ]=25575/512所以,前10个正方形的面积之和为25575/512cm^2.(2)当无限增大时,无限趋近于所有正方形的面积和

人教版高中数学选择性必修二等差数列的前n项和公式(2)教学设计
课前小测1.思考辨析(1)若Sn为等差数列{an}的前n项和,则数列Snn也是等差数列.( )(2)若a1>0,d<0,则等差数列中所有正项之和最大.( )(3)在等差数列中,Sn是其前n项和,则有S2n-1=(2n-1)an.( )[答案] (1)√ (2)√ (3)√2.在项数为2n+1的等差数列中,所有奇数项的和为165,所有偶数项的和为150,则n等于( )A.9 B.10 C.11 D.12B [∵S奇S偶=n+1n,∴165150=n+1n.∴n=10.故选B项.]3.等差数列{an}中,S2=4,S4=9,则S6=________.15 [由S2,S4-S2,S6-S4成等差数列得2(S4-S2)=S2+(S6-S4)解得S6=15.]4.已知数列{an}的通项公式是an=2n-48,则Sn取得最小值时,n为________.23或24 [由an≤0即2n-48≤0得n≤24.∴所有负项的和最小,即n=23或24.]二、典例解析例8.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?分析:将第1排到第20排的座位数依次排成一列,构成数列{an} ,设数列{an} 的前n项和为S_n。

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。

北师大初中七年级数学上册多边形和圆的初步认识教案1
方法总结:在分辨一个图形是否为多边形时,一定要抓住多边形定义中的关键词语,如“线段”“首尾顺次连接”“封闭”“平面图形”等.如此,对于某些似是而非的图形,只要根据定义进行对照和分析,即可判定.探究点二:确定多边形的对角线一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是()A.2015 B.2016 C.2017 D.2018解析:这个多边形的边数为2015+3=2018.故选D.方法总结:过n边形的一个顶点可以画出(n-3)条对角线.本题只要逆向求解即可.探究点三:求扇形圆心角将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,求这三个扇形圆心角的度数.解析:用扇形圆心角所对应的比去乘360°即可求出相应扇形圆心角的度数.解:三个扇形的圆心角度数分别为:360°×22+3+4=80°;360°×32+3+4=120°;

北师大初中七年级数学上册普查和抽样调查教案1
判断下面抽样调查选取样本的方法是否合适:(1)检查某啤酒厂即将出厂的啤酒质量情况,先随机抽取若干箱(捆),再在抽取的每箱(捆)中,随机抽取1~2瓶检查;(2)通过网上问卷调查方式,了解百姓对央视春节晚会的评价;(3)调查某市中小学生学习负担的状况,在该市每所小学的每个班级选取一名学生,进行问卷调查;(4)教育部为了调查中小学乱收费情况,调查了某市所有中小学生.解析:本题应看样本是否为简单随机样本,是否具有代表性.解:(1)合适,这是一种随机抽样的方法,样本为简单随机样本.(2)不合适,我国农村人口众多,多数农民是不上网的,所以调查的对象在总体中不具有代表性.(3)不合适,选取的样本中个体太少.(4)不合适,样本虽然足够大,但遗漏了其他城市里的这些群体,应在全国范围内分层选取样本,除了上述原因外,每班的学生全部作为样本是没有必要的.

北师大初中数学九年级上册线段的比和成比例线段1教案
故线段d的长度为94cm.方法总结:利用比例线段关系求线段长度的方法:根据线段的关系写出比例式,并把它作为相等关系构造关于要求线段的方程,解方程即可求出线段的长.已知三条线段长分别为1cm,2cm,2cm,请你再给出一条线段,使得它的长与前面三条线段的长能够组成一个比例式.解析:因为本题中没有明确告知是求1,2,2的第四比例项,因此所添加的线段长可能是前三个数的第四比例项,也可能不是前三个数的第四比例项,因此应进行分类讨论.解:若x:1=2:2,则x=22;若1:x=2:2,则x=2;若1:2=x:2,则x=2;若1:2=2:x,则x=22.所以所添加的线段的长有三种可能,可以是22cm,2cm,或22cm.方法总结:若使四个数成比例,则应满足其中两个数的比等于另外两个数的比,也可转化为其中两个数的乘积恰好等于另外两个数的乘积.

北师大初中数学九年级上册线段的比和成比例线段2教案
(三)成比例线段的概念1、一般地,在四条线段中,如果 等于 的比,那么这四条线段叫做成比例线段。(举例说明)如:2、四条线段a,b ,c,d成比例,有顺序关系。即a,b,c,d成比例线段,则比例式为:a:b=c:d;a,b, d,c成比例线段,则比例式为:a:b=d:c3思考:a=12,b=8,c=6,d=4成比例吗?a=12,b=8,c=15,d=10呢?三、例题解析: 例1、A、B两地的实际距离AB= 250m,画在一张地图上的距离A'B'=5 cm,求该地图的比例尺。例2:已知,在Rt△ABC中,∠C=90°,∠A=30°,斜边AB=2。求⑴ ,⑵ 四、巩固练习1、已知某一时刻物体高度与其影长的比值为2:7,某 天同一时刻测得一栋楼的影长为30米,则这栋楼的高度为多少?2、某地图上的比例尺为1:1000,甲,乙两地的实际距离为300米,则在地图上甲、乙两地的距离为多少?3、已知线段a,d,b,c是成比例线段,其中a=4,b=5,c=10,求线段d的长。

2023年法治建设工作总结和2024年工作计划汇编(6篇)
四是严格落实公平竞争审查制度。建立健全公平竞争审查机制,印发了《xx经济和信息化局公平竞争审查制度实施方案(试行)》,进一步明确了各科室审查责任和审查内容,坚决不允许出现影响企业公平竞争的限制性措施。今年,共审查规范性文件x件,均未出现影响公平竞争的相关措施。加强对妨碍统一市场、不正当竞争等问题整治,全面落实市场准入负面清单制度。五是持续提升监管效能。全面推行监管执法“一目录,五清单”制度,积极配合州交通局开展“双随机一公开”工作,加强机动车违规改装的监管工作。(三)健全体系,全面推进政府治理规范化程序化法治化一是加强规范性文件清理。全面落实规范性文件合法性审查制度,制定单位规范性文件备案审查程序,未经合法性审查或审查不合法的,不予审议印发。及时制定《州经信局关于开展州政府规章、行政规范性文件清理工作方案》,明确了清理范围、清理标准、方法和责任主体,全面清理了20xx年x月x日至2022年xx月xx日以x府发、x府函、x府办发、x府办函、x府规、x府办规等x种字号印发的州政府文件,共清理非涉密文件xx件,经合法性审核、集体审议,建议废止x件、失效xx件、拟修改x件,继续有效xx件。

巩固和深化ZT教育成果凝聚高质量发展强大力量工作总结
巩固深化ZT教育成果,进一步凝聚推动贵阳高质量发展的强大力量,要求我们坚持不懈在学懂弄通做实新时代中国特色社会主义思想中涵养初心、引领使命,切实做到学思用贯通、知信行统一。要坚持以人民为中心的发展思想,自觉同人民群众想在一起、干在一起,以看得见的变化回应群众期盼。要发扬斗争精神,加强实践锻炼、坚持实干导向,勇于担当作为;要敢于直面问题,勇于自我革命,把全市各级D组织锻造得更加坚强有力。要坚持把“当下改”与“长久立”结合起来,把建章立制和解决问题统一起来,不断巩固深化我市ZT教育成果。守初心、担使命永远在路上。让我们更加紧密地团结在以同志为核心的D中央周围,牢记嘱托守初心、感恩奋进担使命,切实做到一个D员就是一面旗帜,一个支部就是一座堡垒,以坚定不移的决心、坚如磐石的信心、坚持不懈的恒心,坚决打好全面建成小康社会和“十三五”规划收官之战,奋力开创贵阳更加美好的未来。

