-

部编人教版一年级上册《影子》说课稿
【说学法】1.合作学习法。以学生为本、小组合作、生生互助的形式来学习,培养学生在合作中取长补短,互帮互助的合作精神。 同组一起把生字读两遍。然后互相检查看看是否读准字音。并说说自已是怎样记住哪个字的,让学生感受合作学习的快乐。 2.朗读比赛法。为了达到正确、流利地朗读课文的目的。让学生利用多种形式读。如:同桌对读,个别读,小组读等方法,贯穿始终,读中悟,悟中读,收到以读代讲以读悟情的效果。 3.自主评价法。通过让学生自主评价,培养学生倾听,欣赏以及表达能力。从而使低年级学生从小养成学习语文的良好习惯。 五、说教学过程(一)谜语导入,揭示课题1.出示谜语,引出“影子”。? 你有我有他也有,黑身黑腿黑黑头。灯前月下跟你走,就是从来不开口。? (设计意图:猜谜语是小学生喜欢的活动。这个谜语不仅引出了课题,而且呈现了本课要学习的生字,可以给学生一个初步的认识。)

部编人教版三年级上册《灰雀》说课稿
一、说教材 《灰雀》是统编教材小学语文三年级上册第八单元的一篇精读课文,这篇课文讲述的是列宁、灰雀和一个孩子之间的故事。列宁在公园里寻找三只惹人喜爱的灰雀当中的一只时,遇到了将灰雀捉走的男孩,经过交谈,受到感动的男孩将灰雀放了回来。这个故事体现了列宁善解人意,对男孩的尊重、爱护以及男孩的诚实和天真。 通过语言和行动来揭示人物的内心世界,展现事件的发展进程,是本篇课文在表达上的主要特点。男孩的语言和行为已经告诉列宁,灰雀的消失与他有关;如何使孩子认识到将灰雀捉走是错误的从而自愿将小鸟放回来,需要循循善诱。列宁没有问孩子是否将灰雀捉走,也未进行任何说教,而是借助一句“多好的灰雀呀,可惜再也飞不回来了”的感叹,使孩子内心受到震动,从而认识和改正自己的错误。在整个事件中,处处可以发现列宁善于观察对方的言语、行动,既不伤害对方的自尊心,又能使对方认识到错误的巧妙的教育方法,同时,也可以体会到列宁对儿童人格的尊重和爱护。 选编这篇课文的意图,一是要学生认识到列宁对儿童的爱护;二是要通过对人物语言和神态的描写体会人物的心理活动。同时,学生还可以受到爱护鸟类等动物的教育。

部编人教版六年级上册《花之歌》说课稿
一、说教材: 《花之歌》是纪伯伦的散文诗集《泪与笑》中的一首,诗人用花的语言来叙述大自然的话语,文中尽显“纪伯伦风格”中的轻柔、凝练、隽秀与清新。诗人通过花语的倾心流露,构建了一幅大自然活生生的图画,图画中有诗意的浪漫,也有现实的真实,如:“我是诸元素之女:冬将我孕育,春使我开放,夏让我成长,秋令我昏昏睡去”写出了花的成长与芬芳。而“我是亲友之间交往的礼品,我是婚礼的冠冕,我是生者赠予死者最后的祭献”就袒露出了花的凋谢命运,都说纪伯伦的诗有着哲理,寓意深邃,从这就可以看出,诗人是用诗意的叙述和思考的敏锐来书写人生的。 二、说教学目标 1.知识目标: (1)理解、积累本课出现的重点词语。 (2)了解纪伯伦和其艺术风格。 (3)了解课文内容,领悟诗中拟人形象的情感内涵。

部编人教版六年级上册《盼》说课稿(二)
一、说教材 《盼》是统编教材小学语文六年级上册第五单元地第二篇课文,作者是当代女作家铁凝。课文主要讲地是妈妈给“我”买了一件新雨衣,从那以后,“我”每天总是盼着下雨。一天放学后,终于掉了雨点儿,“我”想出各种借口想穿上雨衣到街上去,都没有实现。第二天早晨,“我”背着书包上街,突然掉下了雨点儿。“我”兴奋地跑回家让妈妈帮“我”穿上新雨衣,走在街上,滴答地雨滴让“我”欣喜不已。课文用生动、准确地语言,恰如其分地表达了想要穿上雨衣地“我”对雨天地渴盼、穿着雨衣在在街上行走地快乐。课文为我们呈现了一幅美好地童年生活画面,文中“我”心底地渴盼更能触动孩子们地心灵。同时,文中运用地多种描写方法也能让学生在习作上受到启发。 二、说教学目标 1.会写12个生字,会写“雨衣、袖筒、斗篷”等 词语。 2.能把握课文内容,知道文章是通过哪些事例来写“盼”地。

部编人教版六年级上册《盼》说课稿(一)
【教材分析】《盼》是六年级第五单元的一篇课文。本文选自作家铁凝的第一本出版小说《夜路》,是一篇儿童文学类的小说。作者以孩子的视角,记述了得到新雨衣,渴望下雨到愿望实现——在雨中穿上了新雨衣的故事。用细腻的语言描述了小主人公情感和心理的变化,表现了童真童趣。【教学目标】1.疏通重难点字词的读音和写法。2.整体感知课文内容,把握故事情节,理清行文思路,感受小主人公因新雨衣而产生的“盼”。3.通过捕捉环境描写、人物的语言、动作、神态、对话等描写,来感受小主人公情感的变化。【教学重难点】通过捕捉环境描写、人物的语言、动作、神态、对话等描写,来感受小主人公情感的变化。【教学过程】核心问题:作者如何围绕一个“盼”字展开描写,表现小主人公的情感变化?

部编人教版一年级上册《项链》说课稿
四、说教学重难点1.正确、流利地朗读课文,能合理搭配“的”字词语。(重点)?2.感受大海的美丽,知道大海的项链是什么,体会小娃娃海边玩耍的快乐。(难点)五、说教法和学法俗话说:”教无定法,贵在得法”。教学是师生之间、学生之间交往互动、共同发展的过程。建构主义理论强调以学生为中心,强调学生对知识的主动探索、主动发现和对所学知识的主动建构。在教学这一过程中,学生是学习的中心,教师在整个教学过程中起组织者、指导者、帮助者和促进者的作用。? 因此,遵循学生的认知规律,突出教师为主导,学生为主体的教学原则,本节课主要采用学案导学、闯关游戏、小组竞赛的方式进行学习。教师主要为学生创设问题情境,引导学生在对话、讨论、交流中觅取新知,启发、点拨学生通过分析人物的心理描把握人物形象、领悟小说主旨。为了提高课堂学习效果,主要利用多媒体课件和学案来进行教学。
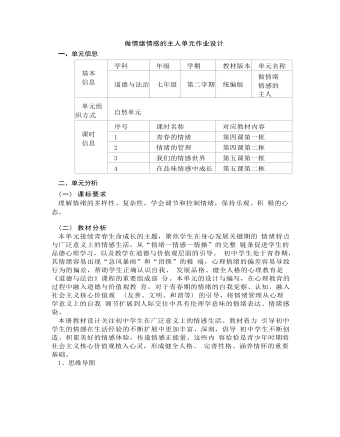
道德与法治七年级下册做情绪情感的主人作业设计
10.阅读材料,回答问题。材料一:近年来,公路上经常出现“路怒族” ,只要看到别人抢道、开车慢、不让道等他们就会 骂人,而且骂得很难听,甚至大打出手。材料二:在新型冠状病毒肺炎疫情防控期间,2020年2月1 日贵州省贵阳市的某商场,一位打扮靓 丽的年轻女子要进入商场时不戴口罩,被商场门口执勤的店员劝阻,要求戴上口罩才能进入商场,该 女子不但不听劝告,而是嗤鼻一笑,不以为然。随后就绕开工作人员打算进入商场,4名工作人员随 后上前阻止,该女子竟然要强行闯入商场,甚至对商场工作人员拳脚相加,随后商场工作人员报警。(1) 结合材料说说,情绪受哪些因素的影响?(2) 根据材料谈谈在生活中如何管理愤怒?11.【东东的日记】下面是东东的“微日记”片段,记录着成长的点滴,与你分享。

道德与法治八年级下册人民当家作主作业设计
①坚持依法行政,维护公平正义②严格遵循诉讼程序,加强立法③司法过程和结果都要合法、公正④坚持以事实为根据,以法律为准绳A.②④ B.②③ C.③④ D.①②3.疫情防控期间,某地检察院充分发挥检察职能,与公安机关等部门加强协作, 提前介入涉疫案件侦查,切实保障人民群众合法权益,全力维护疫情期间社会稳 定。由此可见 ( )①人民检察院是我国的法律监督机关②公安机关是我国的审判机关③公平正义需要法治的保障④人民检察院接受政府的领导和约束A.①② B.①③ C.②③ D.②④(二) 非选择题4. 探究与分享:结合所学知识,与同学讨论探究,回答下列问题。案例反思:2017 年 4 月 20 日,最高人民法院、中央电视台联合公布 2016 年推动法治进程十大案件评选结果,聂某被宣判无罪案等十大案件入选。1995 年 3 月,石家庄中院一审判处聂某死刑,同时判处赔偿受害人家属丧葬费等计 2000 元。1995 年 4 月 27 日,聂某被执行死刑。2016 年 12 月 2 日,最高人民法 院第二巡回法庭宣告撤销原审判决,改判聂某无罪。2017 年 3 月,聂某家属获 268.13991 万元国家赔偿。思考:如何才能避免这种错案的发生?
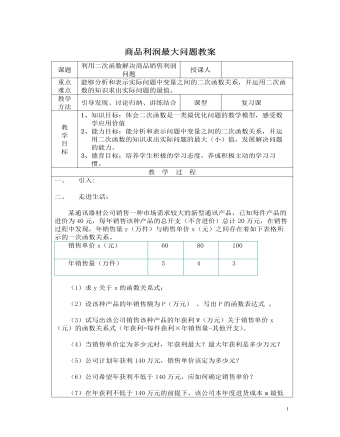
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?
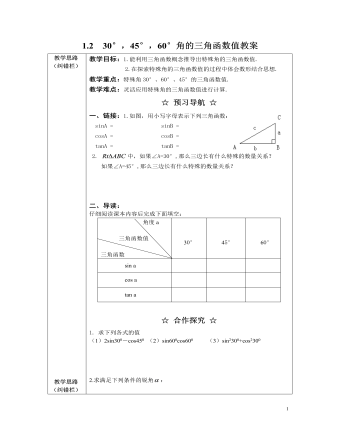
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中九年级数学下册二次函数与一元二次方程2教案
教学目标:1.知道二次函数与一元二次方程的联系,提高综合解决问题的能力.2.会求抛物线与坐标轴交点坐标,会结合函数图象求方程的根.教学重点:二次函数与一元二次方程的联系.预设难点:用二次函数与一元二次方程的关系综合解题.☆ 预习导航 ☆一、链接:1.画一次函数y=2x-3的图象并回答下列问题(1)求直线y=2x-3与x轴的交点坐标; (2)解方程2x-3=0(3)说出直线y=2x-3与x轴交点的横坐标和方程根的关系2.不解方程3x2-2x+4=0,此方程有 个根。二、导读画二次函数y= x2-5x+4的图象1.观察图象,抛物线与x轴的交点坐标是什么?2.求一元二次方程x2-5x+4=0的解。3.抛物线与x轴交点的横坐标与一元二次方程x2-5x+4=0的解有什么关系?(3)一元二次方程ax2+bx+c=0是二次函数y=ax2+bx+c当函数值y=0时的特殊情况.二次函数y=ax2+bx+c的图象与x轴交点的横坐标与一元二次方程ax2+bx+c=0的根有什么关系?

北师大初中七年级数学下册角平分线的性质教案
解析:根据AB∥CD,∠ACD=120°,得出∠CAB=60°.再根据尺规作图得出AM是∠CAB的平分线,即可得出∠MAB的度数.解:∵AB∥CD,∴∠ACD+∠CAB=180°.又∵∠ACD=120°,∴∠CAB=60°.由尺规作图知AM是∠CAB的平分线,∴∠MAB=12∠CAB=30°.方法总结:通过本题要掌握角平分线的作图步骤,根据作图明确AM是∠BAC的角平分线是解题的关键.三、板书设计1.角平分线的性质:角平分线上的点到这个角的两边的距离相等.2.角平分线的作法本节课由于采用了动手操作以及讨论交流等教学方法,从而有效地增强了学生对角以及角平分线的性质的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生在性质的运用上还存在问题,需要在今后的教学与作业中进一步的加强巩固和训练

北师大初中七年级数学下册单项式与单项式相乘教案
解析:先求出长方形的面积,再求出绿化的面积,两者相减即可求出剩下的面积.解:长方形的面积是xym2,绿化的面积是35x×34y=920xy(m2),则剩下的面积是xy-920xy=1120xy(m2).方法总结:掌握长方形的面积公式和单项式乘单项式法则是解题的关键.三、板书设计1.单项式乘以单项式的运算法则:单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里面含有的字母,则连同它的指数作为积的一个因式.2.单项式乘以单项式的应用本课时的重点是让学生理解单项式的乘法法则并能熟练应用.要求学生在乘法的运算律以及幂的运算律的基础上进行探究.教师在课堂上应该处于引导位置,鼓励学生“试一试”,学生通过动手操作,能够更为直接的理解和应用该知识点

北师大初中七年级数学下册等腰三角形的性质教案
方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.三、板书设计1.等腰三角形的性质:等腰三角形是轴对称图形;等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴;等腰三角形的两个底角相等.2.运用等腰三角性质解题的一般思想方法:方程思想、整体思想和转化思想.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中七年级数学下册多项式除以单项式教案
一、情境导入1.计算:(1)-6x3y4z2÷(-23x2y2);(2)9mn÷(-6mn)2·(13n2);(3)6(a-b)3c5÷[-35(a-b)2c]·[-2(a-b)3c4].2.m(a+b+c)=am+bm+cm,(am+bm+cm)÷m=am÷m+bm÷m+cm÷m=a+b+c.你能根据多项式乘以单项式的运算归纳出多项式除以单项式的运算法则吗?二、合作探究探究点:多项式除以单项式【类型一】 直接利用多项式除以单项式进行计算计算:(72x3y4-36x2y3+9xy2)÷(-9xy2).解析:根据多项式除以单项式,先用多项式的每一项分别除以这个单项式,然后再把所得的商相加.解:原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)+9xy2÷(-9xy2)=-8x2y2+4xy-1.方法总结:多项式除以单项式,先把多项式的每一项都分别除以这个单项式,然后再把所得的商相加.

北师大初中七年级数学下册利用“边边边”判定三角形全等教案
解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n边形的一个顶点可以作(n-3)条对角线,把多边形分成(n-2)个三角形,所以,要使一个n边形木架不变形,至少需要(n-3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.三、板书设计1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”.2.三角形的稳定性本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练

北师大初中七年级数学下册利用“边角边”判定三角形全等教案
AD=CD,∠ADE=∠CDG,DE=GD,∴△ADE≌△CDG(SAS),∴AE=CG;(2)设AE与DG相交于M,AE与CG相交于N.在△GMN和△DME中,由(1)得∠CGD=∠AED,又∵∠GMN=∠DME,∠DEM+∠DME=90°,∴∠CGD+∠GMN=90°,∴∠GNM=90°,∴AE⊥CG.三、板书设计1.边角边:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.两边和其中一边的对角对应相等的两个三角形不一定全等.2.全等三角形判定与性质的综合运用本节课从操作探究入手,具有较强的操作性和直观性,有利于学生从直观上积累感性认识,从而有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边角边”掌握较好,但在探究三角形的大小、形状时不会正确分类,需要在今后的教学和作业中进一步加强分类思想的巩固和训练

北师大初中七年级数学下册利用“角边角”“角角边”判定三角形全等教案
1.理解并掌握三角形全等的判定方法——“角边角”“角角边”;(重点)2.能运用“角边角”“角角边”判定方法解决有关问题.(难点) 一、情境导入如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪块去?学生活动:学生先自主探究出答案,然后再与同学进行交流.教师点拨:显然仅仅带①或②是无法配成完全一样的玻璃的,而仅仅带③则可以,为什么呢?本节课我们继续研究三角形全等的判定方法.二、合作探究探究点一:全等三角形判定定理“ASA”如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用“ASA”可得到△ADF≌△CBE.

北师大初中七年级数学下册同底数幂的除法教案
【类型四】 含整数指数幂、零指数幂与绝对值的混合运算计算:-22+(-12)-2+(2015-π)0-|2-π2|.解析:分别根据有理数的乘方、零指数幂、负整数指数幂及绝对值的性质计算出各数,再根据实数的运算法则进行计算.解:-22+(-12)-2+(2015-π)0-|2-π2|=-4+4+1-2+π2=π2-1.方法总结:熟练掌握有理数的乘方、零指数幂、负整数指数幂及绝对值的性质是解答此题的关键.三、板书设计1.同底数幂的除法法则:同底数幂相除,底数不变,指数相减.2.零次幂:任何一个不等于零的数的零次幂都等于1.即a0=1(a≠0).3.负整数次幂:任何一个不等于零的数的-p(p是正整数)次幂,等于这个数p次幂的倒数.即a-p=1ap(a≠0,p是正整数).从计算具体问题中的同底数幂的除法,逐步归纳出同底数幂除法的一般性质.教学时要多举几个例子,让学生从中总结出规律,体验自主探究的乐趣和数学学习的魅力,为以后的学习奠定基础

北师大初中七年级数学下册三角形的内角和教案
解:∵CE⊥AF,∴∠DEF=90°,∴∠EDF=90°-∠F=90°-40°=50°.由三角形的内角和定理得∠C+∠DBC+∠CDB=∠F+∠DEF+∠EDF,又∵∠CDB=∠EDF,∴30°+∠DBC=40°+90°,∴∠DBC=100°.方法总结:本题主要利用了“直角三角形两锐角互余”的性质和三角形的内角和定理,熟记性质并准确识图是解题的关键.三、板书设计1.三角形的内角和定理:三角形的内角和等于180°.2.三角形内角和定理的证明3.直角三角形的性质:直角三角形两锐角互余.本节课通过一段对话设置疑问,巧设悬念,激发起学生获取知识的求知欲,充分调动学生学习的积极性,使学生由被动接受知识转为主动学习,从而提高学习效率.然后让学生自主探究,在教学过程中充分发挥学生的主动性,让学生提出猜想.在教学中,教师通过必要的提示指明学生思考问题的方向,在学生提出验证三角形内角和的不同方法时,教师注意让学生上台演示自己的操作过程和说明自己的想法,这样有助于学生接受三角形的内角和是180°这一结论



