-

诚信教育国旗下讲话稿
记得上一次站在这里,是一年前、国庆长假后的第一次升旗,我自我剖析,现身说法,从爱护我们的眼睛的角度讲如何读书的问题。那次我算是以过来人的身份做自我调侃。时隔一年,今天,我再次站在这里,要讲的却是所有人,尤其是我们的学生和老师,都必须重视的一个话题:诚信。什么是诚信?百度百科中,给的解释是:这是公民的第二张身份证,是为人处事真诚而不虚假,老实而不矫情;是言必行,行必果;是一言九鼎,是一诺千金。甚至有一部同名电视剧,《诚信》。然而,你做到诚信了吗?古有,商鞅立木为信;最近,有下岗女工捡到3万元,在雨中苦等失主3小时归还。遗憾地是,如今,很多人,尤其是学生和老师说,这是傻到家。可你不知,这才是真诚,这才是诚信。

诚信教育国旗下讲话稿
国旗下讲话——诚信尊敬的各位领导、老师、同学们,大家早上好!今天我们的主题是——诚信。先给大家介绍一则小故事。有一天,电视上突然闪现出这样一个画面:一个家伙正面带微笑的亲吻一头驴的屁股!观众们还没有反应过来,电视上就说了,那个亲吻驴屁股的家伙正是nba的老牌球星巴克利,起因是:他曾誓言,说新加盟nba的中国籍球员姚明,如在今后的比赛中,能单场得分超过二十分,他就去亲吻姚明的屁股。在巴克利的球迷看来,这不过是一句戏言。但当姚明真的为休斯敦火箭队拿下三十分后,巴克利即告知媒体,说他决定去亲吻姚明的屁股,是以兑现诺言。且不说姚明是nba的小字辈,就是他所接受的儒家文明,也不允许他去开那样的国际玩笑。在姚明不愿“奉献”屁股的情况下,巴克利变通的跑到乡下,花五百美元买回一头驴,在媒体的监视下,亲吻了那头驴的屁股。同学们,我要说的是巴克利的这种行为正是诚信的行为!何谓诚信呢?忠诚老实,言行一致为诚;遵守诺言,说到做到为信。古今中外,有关诚信的故事不胜枚举。尾生之约让我们感动至今;曾子杀猪告诉今天的父母教育孩子要讲诚信;季布一诺千金和《狼来了》更是我们耳熟能详的诚信故事。有了“诚信”,商鞅的变法得以功成名就,刘邦的约法三章得以千年传为美谈;没有“诚信”,尼克松在“水门事件”中被-迫引咎辞职,克林顿也因在绯闻案中撒谎而险遭弹-劾。

安全教育国旗下的讲话稿
篇同学们!在这个人口密集,面积相对狭小的校园环境里,安全是我们的一直关注的重点。但调查显示,我国中小学生因交通安全、建筑物倒塌、暴力犯罪、食物中毒、溺水等意外事故死亡的人数平均每天有40多人,这些生命的逝去将给家庭带来多大的痛苦!上下楼梯不注意安全发生意外,课间追逐打闹造成骨折,课堂上被铅笔头扎伤、溺水身亡、打架斗殴以及车祸等意外事故令人防不胜防。但研究表明,通过加强自我保护意识,提高自我保护能力,若能在灾难和伤害降临的初期,及时采取正确的措施,80%的伤害是可以避免的。我们小学生正处于生理的发育阶段,心理非常单纯,最容易受到各种各样的伤害。但是,生命总是眷顾有安全意识的人,而安全意识是从日常行为中体现出来的。比如:遵纪守法,遵守交通规则,不做危及安全的游戏,不携带锋利的危险物品进校园,遇事冷静,做事多想想后果要三思而行,同学间有了矛盾要冷静解决,不要鲁莽行事。这些知识很简单,但如果做不到,我们的健康甚至生命就可能受到威胁。这段时间来学校就发生了好几起安全事故:有在课间追逐与同学相撞流血的;有爬高低杠摔下来导致骨折的;有走路不小心被车撞的手折的;有做事粗心被压伤手指的;有为抢着打乒乓球而打架的;有带一些塑料的刀具进校园弄伤同学的。在站的各位同学,大家看看那几个扎着白色绷带的受伤同学,我们要引以为鉴,要自觉遵守学校的安全常规,时刻牢记“安全至上”的理念。

安全教育国旗下讲话稿
老师们,同学们:大家早上好!今天我国旗下讲话的内容是安全法制教育。在日常生活中,我们从事的各种活动都有可能遇到各种不安全的因素甚至造成严重安全事故。据了解,我国每年有近万中小学生因交通事故、食物中毒、溺水等原因非正常死亡。非正常死亡的中小学生平均每天达40多人,而其中位居首位的,就是交通死亡人数。在现实生活中,当我们走在马路上,会时不时地发现有人闯红灯,有人逆行车,有人边骑车边听音乐,有人骑车带人等违反交通规则,危害交通安全的不良行为。在这里,我要郑重地提醒我们的同学为确保我们自身的生命安全,也为了维护良好的交通秩序,做到不闯红灯外,骑自行车时不要带人,不要多人并排骑车,更不要逆行车。在我们的校园内,同样也存在着很多威胁着我们人身和财产安全的现象。有的同学在楼道里嬉戏追赶,上下楼时互相打闹;有的同学在运动时不注意自我保护而受伤;有的同学不能正确处理同学之间的矛盾,打架斗殴等。在这里我要提醒同学们的是要遵守学校的有关规章制度,增强自我保护意识。

安全教育日国旗下的讲话稿
以下是关于安全教育日国旗下的讲话稿的文章!安全教育日国旗下的讲话稿老师们、同学们:三月,是春风和煦、万木吐绿的美好季节,俗话说:“一年之际在于春。”人们把许多纪念日都放在了三月,如: 3月5日“向雷锋同志学习”纪念日,3月8日国际劳动妇女节,3月12日中国植树节,3月15日国际消费者权益日,3月21日世界睡眠日,3月22日世界水日,3月23日世界气象日。今天我讲的是大家可能还不太熟悉的一个纪念日:那就是全国中小学安全宣传教育日。国家有关部门规定每年三月最后一周的星期一作为全国中小学生“安全教育日”。

法制教育国旗下讲话稿
同学们:大家好!今天,很高兴能和同学们在一起共同进行一次法制学习。其实,有些法律知识我应该向你们学习的,为什么呢?前不久,我陪同市领导到校调研的时候,观看了同学们自己编写的法制小故事,很真实,很深刻。其中有一位同学编写的一个毛阿敏偷税漏税的故事,我深受启发,这不仅仅是一个故事,而是你们的内心深处法律意识的真实反映。在这里,我也给大家讲一个我亲眼目睹、令人深思的真人真事。事情发生在四小区的住宅楼,这天正是星期日,三位初中生在四楼的楼道窗前嬉戏,甲失手将乙推出窗外,重重地从高达20米的四楼摔了下来。当时乙的脸色铁青,血从鼻孔、耳孔直往外淌。后来,乙被市医院急救车救走。此时,我给同学们出二个思考题:①甲失手致伤乙,算不算违法?②如果甲违法,违反了什么法?结果应是:如果医疗签定部门确定为重伤,首先甲这种行为造成的后果违法,其次甲违反了《刑法》第四章侵犯公民人身权利,民主权利罪第二百三十五条:过失伤害他人致人重伤,处三年以下有期徒刑或拘役。

感恩教育国旗下讲话稿
感恩教育国旗下讲话稿一:开始演讲之前,我想请同学们思考一下,不知大家有没有统计过,到目前为止,你一共接受过多少位老师的教诲,或者,你还记得过去哪些老师的音容笑貌。有人可能会很随意地回一句“我早就忘了”。也难怪,因为他们都是平凡的人,从事的是平凡的职业,做的是平凡的事,正因如此,他们就像我们的家人一样常常被我们理所当然地忽略了。也有些人,他们对他们过去的老师仍然记忆犹新,那是因为,他们同时又是不平凡的,他们担负着启迪、引领我们的责任,他们对我们倾注了无限的爱,对我们的关心和了解甚至超过了我们的家人,比我们的父母更为我们的成长操心。正是因为有这些既平凡又不平凡的人的默默奉献,才有了今天这个特别的日子:感恩节和教师节。我想,教师节,同时也应该是我们莘莘学子们回报老师的感恩节。你有没有发现,每天放学后,天都黑下来了,年段办公室里还有不少迟归的老师们忙碌的身影;你想没想过,夜深人静,当你已经进入甜美的梦乡,老师仍在灯下紧张地备课、批改作业的情形;你知不知道,孩子生病时,老师顾不上带他去看病扔在托儿所里,自己却赶到学校来为学生上课、辅导的事;你听没听过,把被父母遗弃的学生带到家里,给他吃住陪他读书,使他顺利通过会考的老师;你经没经历过,老师的家人牺牲休息时间,亲自开车护送老师们挨家挨户家访的事……我们见到、听说、经历的何止这些。这就是我们时代中学的老师,比别的学校的老师付出得、。演讲稿

爱校教育国旗下讲话稿
讲话稿有广义和狭义之分。广义的讲话稿是人们在特定场合发表讲话的文稿;狭义的讲话稿即一般所说的领导讲话稿,是各级领导在各种会议上发表带有宣传、指示、总结性质讲话的文稿。是应用写作研究的重要文体之一。表明事情的缘由。下面是爱校教育国旗下讲话稿,请参考!爱国爱校国旗下讲话稿: 尊敬的老师,亲爱的同学们:大家早上好!我是高二班的x,我是高二班的xx,今天我们国旗下演讲的题目组是《爱国铭记心中,爱校落实行动》。祖国,一个神圣庄严的称呼,一种伟大力量的凝聚,一种深厚感情的沉淀。在祖国曲折发展的历史过程中,爱国历来是人民所推崇的最高精神。爱国者无所畏惧,将国家的荣誉和利益看得比自己的生命更重要。苟利国家生死以,岂因祸福避趋之。正是这样的爱国主义精神才让中国人民站起来了,正是这种精神才让中华民族生生不息。二十一世纪的今天,我们祖国日益繁荣昌盛,爱国主义更应该是这个时代最强的,最令人震撼的音符。爱国不能是一个空泛的名词,更不应该是一句空洞的口号。对我们每一位学生来说,爱国应该从爱校做起。

北师大初中七年级数学上册利用移项与合并同类项解一元一次方程教案2
练习:现在你能解答课本85页的习题3.1第6题吗?有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果送还了一条船 ,正好每条船坐9人,问这个班共多少同学?小结提问:1、今天你又学会了解方程的哪些方法?有哪些步聚?每一步的依据是什么?2、现在你能回答前面提到的古老的代数书中的“对消”与“还原”是什么意思吗?3、今天讨论的问题中的相等关系又有何共同特点?学生思考后回答、整理:① 解方程的步骤及依据分别是:移项(等式的性质1)合并(分配律)系数化为1(等式的性质2)表示同一量的两个不同式子相等作业:1、 必做题:课本习题2、 选做题:将一块长、宽、高分别为4厘米、2厘米、3厘米的长方体橡皮泥捏成一个底面半径为2厘米的圆柱,它的高是多少?(精确到0.1厘米)

北师大初中数学九年级上册用因式分解法求解一元二次方程2教案
【学习目标】1 、学习过程与方法:因式分解法是把一个一元二次方程化为两个一元一次方程来解,体现了一种“降次”思想、“转化”思想,并了解这种转化思想在解方程中的应用。2、学习重点 :用因式分解法解某些方程。 【温故】1、(1)将一个多项式(特别是二次三项式)因式分解,有哪几种分解方法?(2)将下列多项式因式分解① 3x2-4x ② 4x2-9y2 ③x2- 6xy+9y2④ (2x+1)2+4(2x+1)+4 【知新】1.自学课本 P46----P48[讨论]以上解方程的方法是如何使二次方程降为一次的?2、用分解因式法 解方程例1、解下 列方程(1)3 x2-5x=0 (2)x(x-2) +x-2=0例2、用因式分解法解下列方程 (1)5x2-2x-1/4=x2-2x+3/4 (2)x(x-3)-4( 3-x)=0 (3)(5-x)2-16=0 (4)16(2x-1)2=25(x-2)2

北师大初中七年级数学上册利用移项与合并同类项解一元一次方程教案1
(3)移项得-4x=4+8,合并同类项得-4x=12,系数化成1得x=-3;(4)移项得1.3x+0.5x=0.7+6.5,合并同类项得1.8x=7.2,系数化成1得x=4.方法总结:将所有含未知数的项移到方程的左边,常数项移到方程的右边,然后合并同类项,最后将未知数的系数化为1.特别注意移项要变号.探究点三:列一元一次方程解应用题把一批图书分给七年级某班的同学阅读,若每人分3本,则剩余20本,若每人分4本,则缺25本,这个班有多少学生?解析:根据实际书的数量可得相应的等量关系:3×学生数量+20=4×学生数量-25,把相关数值代入即可求解.解:设这个班有x个学生,根据题意得3x+20=4x-25,移项得3x-4x=-25-20,合并同类项得-x=-45,系数化成1得x=45.答:这个班有45人.方法总结:列方程解应用题时,应抓住题目中的“相等”、“谁比谁多多少”等表示数量关系的词语,以便从中找出合适的等量关系列方程.

北师大初中七年级数学上册应用一元一次方程——“希望工程”义演教案1
方法总结:解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程再求解.探究点三:工程问题一个道路工程,甲队单独施工9天完成,乙队单独做24天完成.现在甲乙两队共同施工3天,因甲另有任务,剩下的工程由乙队完成,问乙队还需几天才能完成?解析:首先设乙队还需x天才能完成,由题意可得等量关系:甲队干三天的工作量+乙队干(x+3)天的工作量=1,根据等量关系列出方程,求解即可.解:设乙队还需x天才能完成,由题意得:19×3+124(3+x)=1,解得:x=13.答:乙队还需13天才能完成.方法总结:找到等量关系是解决问题的关键.本题主要考查的等量关系为:工作效率×工作时间=工作总量,当题中没有一些必须的量时,为了简便,应设其为1.三、板书设计“希望工程”义演题目特点:未知数一般有两个,等量关系也有两个解题思路:利用其中一个等量关系设未知数,利用另一个等量关系列方程

北师大初中七年级数学上册应用一元一次方程——水箱变高了教案2
从而为列方程找等量关系作了铺垫.环节2中的表格发给每个小组,为增强小组讨论结果的展示起到了较好的作用.环节3中通过让学生自己设计表格为讨论的得出起到辅助作用.2.相信学生并为学生提供充分展示自己的机会本节课的设计中,通过学生多次的动手操作活动,引导学生进行探索,使学生确实是在旧知识的基础上探求新内容,探索的过程是没有难度的任何学生都会动手操作,每个学生都有体会的过程,都有感悟的可能,这种形式让学生切身去体验问题的情景,从而进一步帮助学生理解比较复杂的问题,再把实际问题抽象成数学问题.3.注意改进的方面本节课由于构题新颖有趣,所以一开始就抓住了学生的求知欲望,课堂气氛活跃,讨论问题积极主动.但由于学生发表自己的想法较多,使得教学时间不能很好把握,导致课堂练习时间紧张,今后予以改进.

北师大初中七年级数学上册应用一元一次方程——“希望工程”义演教案2
1:甲、乙、丙三个村庄合修一条水渠,计划需要176个劳动力,由于各村人口数不等,只有按2:3:6的比例摊派才较合理,则三个村庄各派多少个劳动力?2:某校组织活动,共有100人参加,要把参加活动的人分成两组,已知第一组人数比第二组人数的2倍少8人,问这两组人数各有多少人?目的:检测学生本节课掌握知识点的情况,及时反馈学生学习中存在的问题.实际活动效果:从学生做题的情况看,大部分学生都能正确地列出方程,但其中一部分人并不能有意识地用“列表格”法来分析问题,因此,教师仍需引导他们能学会用“列表格”这个工具,有利于以后遇上复杂问题能很灵活地得到解决.六、归纳总结:活动内容:学生归纳总结本节课所学知识:1. 两个未知量,两个等量关系,如何列方程;2. 寻找中间量;3. 学会用表格分析数量间的关系.

北师大初中七年级数学上册应用一元一次方程——水箱变高了教案1
解:设截取圆钢的长度为xmm.根据题意,得π(902)2x=131×131×81,解方程,得x=686.44π.答:截取圆钢的长度为686.44πmm.方法总结:圆钢由圆柱形变成了长方体,形状发生了变化,但是体积保持不变.“变形之前圆钢的体积=变形之后长方体的体积”就是我们所要寻找的等量关系.探究点三:面积变化问题将一个长、宽、高分别为15cm、12cm和8cm的长方体钢坯锻造成一个底面是边长为12cm的正方形的长方体钢坯.试问:是锻造前的长方体钢坯的表面积大,还是锻造后的长方体钢坯的表面积大?请你计算比较.解析:由锻造前后两长方体钢坯体积相等,可求出锻造后长方体钢坯的高.再计算锻造前后两长方体钢坯的表面积,最后比较大小即可.解析:设锻造后长方体的高为xcm,依题意,得15×12×8=12×12x.解得x=10.锻造前长方体钢坯的表面积为2×(15×12+15×8+12×8)=2×(180+120+96)=792(cm2),锻造后长方体钢坯的表面积为2×(12×12+12×10+12×10)=2×(144+120+120)=768(cm2).
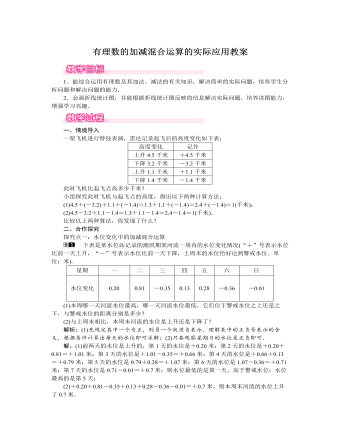
北师大初中七年级数学上册有理数的加减混合运算的实际应用教案
(1)本周哪一天河流水位最高,哪一天河流水位最低,它们位于警戒水位之上还是之下,与警戒水位的距离分别是多少?(2)与上周末相比,本周末河流的水位是上升还是下降了?解析:(1)先规定其中一个为正,则另一个就用负表示.理解表中的正负号表示的含义,根据条件计算出每天的水位即可求解;(2)只要观察星期日的水位是正负即可.解:(1)前两天的水位是上升的,第1天的水位是+0.20米;第2天的水位是+0.20+0.81=+1.01米;第3天的水位是+1.01-0.35=+0.66米;第4天的水位是+0.66+0.13=+0.79米;第5天的水位是0.79+0.28=+1.07米;第6天的水位是1.07-0.36=+0.71米;第7天的水位是0.71-0.01=+0.7米;则水位最低的是第一天,高于警戒水位;水位最高的是第5天;(2)+0.20+0.81-0.35+0.13+0.28-0.36-0.01=+0.7米,则本周末河流的水位上升了0.7米.方法总结:解此题的关键是分析题意列出算式,用的数学思想是转化思想,即把实际问题转化成数学问题.探究点二:有理数的加减混合运算在生活中的其他应用

北师大初中数学九年级上册利用一元二次方程解决面积问题2教案
四.知识梳理谈谈用一元二次方程解决例1实际问题的方法。五、目标检测设计1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为( ).【设计意图】发现几何图形中隐蔽的相等关系.2.镇江)学校为了美化校园环境,在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃.(1)若请你在这块空地上设计一个长方形花圃,使它的面积比学校计划新建的长方形花圃的面积多1平方米,请你给出你认为合适的三种不同的方案.(2)在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.【设计意图】考查学生的审题能力及用一元二次方程模型解决简单的图形面积问题.

北师大初中数学九年级上册几何问题及数字问题与一元二次方程1教案
解:设个位数字为x,则十位数字为14-x,两数字之积为x(14-x),两个数字交换位置后的新两位数为10x+(14-x).根据题意,得10x+(14-x)-x(14-x)=38.整理,得x2-5x-24=0,解得x1=8,x2=-3.因为个位数上的数字不可能是负数,所以x=-3应舍去.当x=8时,14-x=6.所以这个两位数是68.方法总结:(1)数字排列问题常采用间接设未知数的方法求解.(2)注意数字只有0,1,2,3,4,5,6,7,8,9这10个,且最高位上的数字不能为0,而其他如分数、负数根不符合实际意义,必须舍去.三、板书设计几何问题及数字问题几何问题面积问题动点问题数字问题经历分析具体问题中的数量关系,建立方程模型解决问题的过程,认识方程模型的重要性.通过列方程解应用题,进一步提高逻辑思维能力和分析问题、解决问题的能力.经历探索过程,培养合作学习的意识.体会数学与实际生活的联系,进一步感知方程的应用价值.

北师大初中数学九年级上册营销问题及平均变化率问题与一元二次方程2教案
5.一件上衣原价每件500元,第一次降价后,销售甚慢,第二次大幅度降价的百分率是第一次的2 倍,结果以每件240元的价格迅速出售,求每次降价的百分率是多少?6.水果店花1500元进了一批水果,按50%的利润定价,无人购买.决定打折出售,但仍无人购买,结果又一次打折后才售完.经结算,这批水果共盈利500元.若两次打折相同,每次打了几折?(精确到0.1折)7.某服装厂为学校艺术团生产一批演出服,总成本3000元,售价每套30元.有24名家庭贫困学生免费供应.经核算,这24套演出服的成本正好是原定生产这批演出服的利润.这批演出服共生产了多少套?8、某商店经营T恤衫,已知成批购进时单价是2.5元。根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售200件。请你帮助分析,销售单价是多少时 ,可以获利9100元?

北师大初中数学九年级上册用配方法求解简单的一元二次方程1教案
探究点二:用配方法解二次项系数为1的一元二次方程用配方法解方程:x2+2x-1=0.解析:方程左边不是一个完全平方式,需将左边配方.解:移项,得x2+2x=1.配方,得x2+2x+(22)2=1+(22)2,即(x+1)2=2.开平方,得x+1=±2.解得x1=2-1,x2=-2-1.方法总结:用配方法解一元二次方程时,应按照步骤严格进行,以免出错.配方添加时,记住方程左右两边同时加上一次项系数一半的平方.三、板书设计用配方法解简单的一元二次方程:1.直接开平方法:形如(x+m)2=n(n≥0)用直接开平方法解.2.用配方法解一元二次方程的基本思路是将方程转化为(x+m)2=n(n≥0)的形式,再用直接开平方法,便可求出它的根.3.用配方法解二次项系数为1的一元二次方程的一般步骤:(1)移项,把方程的常数项移到方程的右边,使方程的左边只含二次项和一次项;(2)配方,方程两边都加上一次项系数一半的平方,把原方程化为(x+m)2=n(n≥0)的形式;(3)用直接开平方法求出它的解.

