-

中班科学课件教案:好听的声音
2、初步了解同种物体,由于数量的多少,发出的声音也不同。3、初步尝试用不同声音的套桶为乐曲伴奏。4、培养幼儿的操作兴趣。 活动准备:1、人手一个套桶娃娃,蚕豆、米、绿豆等若干。2、《小手爬》的音乐,透明的瓶子若干。 活动过程:一、引导幼儿让套桶发出声音。 出示空套桶,“今天套桶娃娃想和我们小朋友做游戏。” 教师摇动空套桶,“你们听,怎么没声音?”1、教师设问: 你有什么办法让空套桶发出声音?(在套桶里装上东西)“我们一起动手让套桶娃娃发出好听的声音,在你的套桶里装上一样东西,盖好,握握紧,摇一摇、听一听。” 幼儿探索、操作。

中班科学课件教案:电筒亮了
2、乐意参加安装电池的探索活动,感受成功的乐趣。3、愿意与同伴一起操作、交流。活动准备:常用电池若干个(1、2、5、7号,)大小不同的电筒若干个(分别使用1号、2号及5号电池)录音机、磁带 黑猫警长图片电视机、视频转换仪 活动过程:一、通过观察、比较,了解常用电池的外形特征,尝试从多角度发现电池的差异。1、 幼儿观察操作材料:“桌子上有什么?”(电池)“这些电池一样吗?”(不一样)“它们有那些地方不一样?请你从篮子里分别拿两个不一样的电池来比一比,找一找。”

中班科学课件教案:会“跳”的豆子
[活动准备] 高脚杯6个、黄豆若干、大铁盘6个、记录白纸30张、铅笔30支。 [活动过程] 探究的问题:把黄豆放到高脚杯里,要装得满满的,然后加入少量清水,再将酒杯放在大铁盘上,看看有什么变化? 幼儿讨论。(1)豆子被泡大了。

中班科学课件教案:冬天趣事多
塑料尺只要我们往身上的毛衣上一擦,它好像就突然具有了神奇的魔力一样,能吸引起小纸屑,真是很有意思。日常生活中,还有什么东西擦一下就能产生神奇的魔力呢?本节课的活动目的不是认识静电,而是告诉幼儿,我们只有细心观察、乐于探索,就会在我们身边发现无穷无尽的乐趣。只有对我们世界产生好奇的人,才有可能对科学产生兴趣。※ 活动目标1 观察毛衣摩擦产生的现象2 激发幼儿喜欢做小试验的兴趣3 尝试作记录※ 活动准备纸屑、记录纸旧毛衣、塑料尺、塑料棒、铅笔、木筷子、记录表、木梳子、塑料梳子、木棒等※ 活动过程预备活动:安静游戏《小鸟小鸟》1 创设情境,吸引幼儿注意力,引发幼儿思考师:老师手里面握住的是天空,小小的桌子是大地,冬天来了,天空上飘下了美丽的雪花!小朋友,想不想把小雪花拣起来玩啊?幼:想。发现更多的东西能摩擦后互相吸引,就告诉

中班科学课件教案:稻子和麦子
2、体验秋天丰收的喜悦 活动准备:稻子、麦子实物和图片等 活动过程: 一、 认识稻子和麦子 1、引出:这几天呀,农民伯伯很开心,他们种的庄稼都丰收了。请你们来说说秋天有哪些庄稼丰收了? ——————稻子、玉米、棉花、各种豆……. 2、FLASH欣赏:丰收的秋天 (加入动作) 小结:秋天有很多庄稼都丰收了,有稻子、棉花…..,真是个收获的季节! 3.可是呀,农民伯伯遇上了一个难题,他呀分不出稻子和麦子,让我们来帮帮他吧。 (分稻子和麦子)说说稻子和麦子有什么不同?(图片) ————稻子长的弯弯的,象……/麦子长的直直的,象…… (稻穗和麦穗)

中班科学:水果里的图案课件教案
活动准备: 各种常见水果若干、布袋、塑料水果刀、盘子、猕猴桃、黄桃、圣女果活动过程:一、摸水果 教师出示装有各种幼儿熟悉的水果的自制摸宝袋,请幼儿摸摸、说说自己从袋里摸到的是什么水果,它的外形是怎样的?它的味道如何?有没有香味?二、出示水果图案 教师出示某一水果的切面,请幼儿观察它的图案。

中班科学《有趣的磁铁》课件教案
活动目标:1、让幼儿初步了解磁铁的基本特性2、了解磁铁在生活中的用途3、培养幼儿的探索兴趣 活动过程:一引题师:小朋友,今天老师要带你们去一个很好玩的地方,但是去那个地方玩我们小朋友都要带上一样东西才能进去,我们看看我们要带什么东西进去?(教师出示磁铁)幼:磁铁师:现在小朋友们可以拿着磁铁进去玩了?你们看看会发生什么事?幼:好师:小朋友看看为什么磁铁吸不住这个东西啊?幼:因为它是木头的师:小朋友聪明,那你们看看磁铁为什么又不能吸住这个东西呢?幼:因为它是塑料的

肺炎疫情防控个人工作讲话心得新版多篇
发挥“集聚效应”,让人才“待得住”。引进人才待遇固然重要,但用票子、房子、位子、“帽子”留人总是暂时的,而营造一个创业有机会、干事有舞台、发展有空间的“软环境”,才是招才引智的长久之计。当前,一些地方在招才过程中重物质轻感情,简单粗暴的在物质条件改善上盲目投资,却严重缺乏与人才的情感交流;有的地方在社会保障、公共服务、干事创业等软件方面有比较明显的欠缺,人才引进后又流失的现象时有发生。各级各地要大兴惜才爱才敬才之风,学会在感情投入上做文章,多往人才那儿跑一跑,多和人才交交心,举办人才交流座谈会,及时了解人才的内心状况,营造更加尊重知识、尊重人才的良好氛围。要加强关心关爱,做细服务保障平台,为人才提供针对性、个性化、跟踪式的精准服务,切实解除其在艰苦边远地区和基层一线干事创业的后顾之忧,提升艰苦边远地区和基层一线的人才聚集力,让人才价值得到充分尊重和实现。

部编版语文九年级上册《论教养》教案
一、导入新课教养,是表现在行为方式中的道德修养状况,是社会影响、家庭教育、学校教育、个人修养的结果。中国是文明古国,礼仪之邦,关于“教养”,中国古时《三字经》就提到了,指的是人从小就应该习得的一种规矩,待人接物处事时的一种敬重态度。今天我们学习利哈乔夫的《论教养》,进一步理解教养的核心内涵以及学习如何做一个有教养的人。【教学提示】设计学生感兴趣的话题,引发学生的思考和关注,为学生更好地学习本文奠定基础。二、教学新课目标导学一:初读课文,理清层次1.指导学生朗读课文。朗读指导:抓住议论性的句子,把握作者的观点,理解观点和材料之间的关系。2.小组讨论。给课文划分层次,理清作者思路,理解议论文结构的一般特点。明确:第一部分(1—2):开门见山,引入论题——良好的教养。第二部分(3—12):把有无教养的表现进行对比,指出教养的思想核心是尊重他人。第三部分(13—17):剖析优雅风度,指出一切优雅风度的基础其实是一种关照态度。

幼儿园中班安全教案:认标志,讲安全
[活动目标]1、鼓励幼儿在生活中做一个善于观察的有心人。2、进一步培养幼儿的语言表达能力、观察能力、思维想象力和分析能力。3、帮助幼儿认识生活中的一些常见标志,懂得基本的安全知识,提高自我保护能力。[活动准备]1、请家长协助带孩子在生活中观察常见的安全标志。2、各种标志、图片若干。3、布置好的“安全标志图片展览”4、音乐磁带。[活动过程] 一、教师组织幼儿在音乐声中进入活动室,并参观布置好的“安全标志图片展览”幼儿边看边说说自己认识哪些标志,它们有什么意义。(评析:幼儿在音乐声中进入活动,会有一个轻松愉快的开始,为活动打好铺垫。参观图片展,能给幼儿一个整体的印象,他们在看看说说的过程中,会互相学习,这也体现了纲要中提到的“注重幼儿间的相互作用”)
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。
人教A版高中数学必修二古典概型和概率的基本性质教学设计
新知讲授(一)——古典概型 对随机事件发生可能性大小的度量(数值)称为事件的概率。我们将具有以上两个特征的试验称为古典概型试验,其数学模型称为古典概率模型,简称古典概型。即具有以下两个特征:1、有限性:样本空间的样本点只有有限个;2、等可能性:每个样本点发生的可能性相等。思考一:下面的随机试验是不是古典概型?(1)一个班级中有18名男生、22名女生。采用抽签的方式,从中随机选择一名学生,事件A=“抽到男生”(2)抛掷一枚质地均匀的硬币3次,事件B=“恰好一次正面朝上”(1)班级中共有40名学生,从中选择一名学生,即样本点是有限个;因为是随机选取的,所以选到每个学生的可能性都相等,因此这是一个古典概型。
人教A版高中数学必修二平面与平面平行教学设计
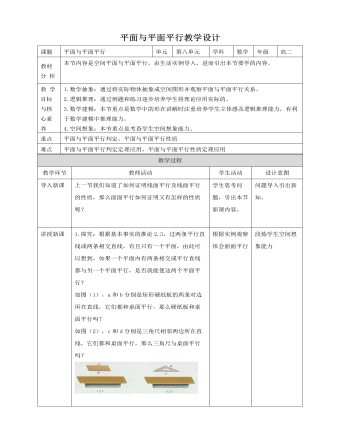
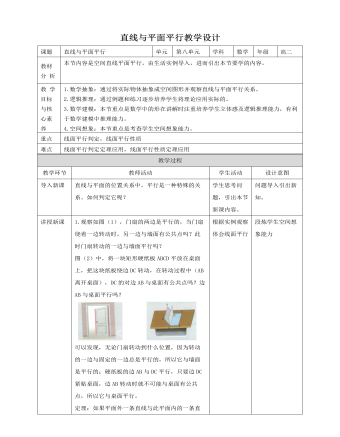
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
人教A版高中数学必修二事件的相互独立性教学设计
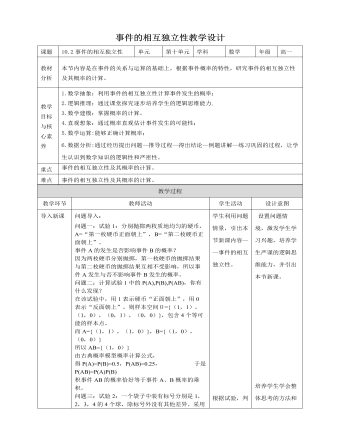
问题导入:问题一:试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。事件A的发生是否影响事件B的概率?因为两枚硬币分别抛掷,第一枚硬币的抛掷结果与第二枚硬币的抛掷结果互相不受影响,所以事件A发生与否不影响事件B发生的概率。问题二:计算试验1中的P(A),P(B),P(AB),你有什么发现?在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则样本空间Ω={(1,1),(1,0),(0,1),(0,0)},包含4个等可能的样本点。而A={(1,1),(1,0)},B={(1,0),(0,0)}所以AB={(1,0)}由古典概率模型概率计算公式,得P(A)=P(B)=0.5,P(AB)=0.25, 于是 P(AB)=P(A)P(B)积事件AB的概率恰好等于事件A、B概率的乘积。问题三:试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。
人教A版高中数学必修二圆柱、圆锥、圆台和球的表面积与体积教学设计
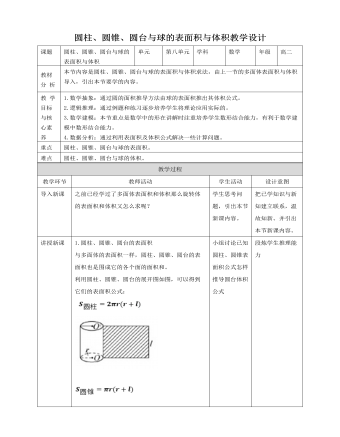
1.圆柱、圆锥、圆台的表面积与多面体的表面积一样,圆柱、圆锥、圆台的表面积也是围成它的各个面的面积和。利用圆柱、圆锥、圆台的展开图如图,可以得到它们的表面积公式:2.思考1:圆柱、圆锥、圆台的表面积之间有什么关系?你能用圆柱、圆锥、圆台的结构特征来解释这种关系吗?3.练习一圆柱的一个底面积是S,侧面展开图是一个正方体,那么这个圆柱的侧面积是( )A 4πS B 2πS C πS D 4.练习二:如图所示,在边长为4的正三角形ABC中,E,F分别是AB,AC的中点,D为BC的中点,H,G分别是BD,CD的中点,若将正三角形ABC绕AD旋转180°,求阴影部分形成的几何体的表面积.5. 圆柱、圆锥、圆台的体积对于柱体、锥体、台体的体积公式的认识(1)等底、等高的两个柱体的体积相同.(2)等底、等高的圆锥和圆柱的体积之间的关系可以通过实验得出,等底、等高的圆柱的体积是圆锥的体积的3倍.
人教A版高中数学必修二总体集中趋势的估计教学设计
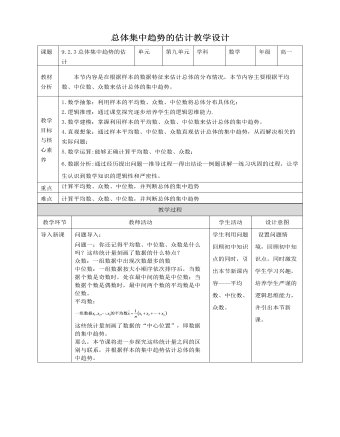
(2)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下。故用中位数来估计每天的用水量更合适。1、样本的数字特征:众数、中位数和平均数;2、用样本频率分布直方图估计样本的众数、中位数、平均数。(1)众数规定为频率分布直方图中最高矩形下端的中点;(2)中位数两边的直方图的面积相等;(3)频率分布直方图中每个小矩形的面积与小矩形底边中点的横坐标之积相加,就是样本数据的估值平均数。学生回顾本节课知识点,教师补充。 让学生掌握本节课知识点,并能够灵活运用。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

