-

小班科学教案 有趣的肥皂
[活动目标] 1、培养幼儿用肥皂洗手的良好卫生习惯。 2、通过幼儿的自主探索活动,使幼儿知道肥皂的外形特征及用途。 [活动准备] 各式各样的肥皂及肥皂盒若干;各种旧玩具、旧手绢等;吹泡泡玩具瓶(与幼儿人数相等);“我爱洗澡”音乐及磁带、录音机;盛玩具的小筐若干;干净毛巾(与幼儿人数相等)、盛水的大水盆六个,小方布一块,剪好的小红星若干。 [活动过程]1、《我爱洗澡》音乐,老师与幼儿做动作进入活动室。 (1)老师吹泡泡引起幼儿兴趣。 (2)出示肥皂并请幼儿描述。(请幼儿自由发言) (3)出示多种多样的肥皂,让幼儿观摩。老师引导幼儿观察肥皂形状、颜色、气味,并用手摸摸,说出感觉。(幼儿分别发表自己的意见)

关于勤学与成才的国旗下的讲话
同学们:我们应该懂得学习对我们来说是一种需要,是我们实现理想的途径,勤学更是我们成材唯一的有效途径。任何学习意识的形成,首先应培养良好的动机,正像机器要有发动机一样,每种学习的行动的后面都有一种动力,就像发动机一样,它的功率越大,机器的动力就越大,而学习的动力越强,学习的自觉性和积极性就越高。没有这个马达,学习也就无从谈起。学习意识的形成,还需激发强烈的学习兴趣和提高“会学”的能力。“会学”能力的形成并非易事,我们知道:学习是一项艰苦的脑力劳动,任何学习成果的获得都不是朝夕可成,一蹴而就。然而有些同学终日做着“成材梦”,却不肯付诸行动去学习;羡慕那些盛开的花朵,却不用辛勤的汗水去浇灌它,空有“天生我才必有用”的想法,结果只是黄梁美梦一场空。

中班科学课件教案:会变的水
准备小容器、蜡烛、颜料等若干份,图书《小水滴旅行》(人民教育出版社出版“萤火虫”画丛)。过程活动(一)冻冰花1.带领幼儿在院子里或幼儿园附近寻找结冰的地方。师生一起在一块平坦的土地上泼一些水,建造一个小小滑冰场。让幼儿在自己建的小冰场上滑冰、拉冰车,充分地感知冰的特性(凉、滑、硬、脆),享受冰上游戏的快乐。中循环

人教版新课标高中物理必修1用牛顿运动定律解决问题(二)说课稿2篇
教师活动:(1)组织学生回答相关结论,小组之间互相补充评价完善。教师进一步概括总结。(2)对学生的结论予以肯定并表扬优秀的小组,对不理想的小组予以鼓励。(3)多媒体投放板书二:超重现象:物体对支持物的压力(或对悬挂物的拉力)大于物体所受到的重力的情况称为超重现象。实质:加速度方向向上。失重现象:物体对支持物的压力(或对悬挂物的拉力)小于物体所受到的重力的情况称为失重现象。实质:加速度方向向下。(4)运用多媒体展示电梯中的现象,引导学生在感性认识的基础上进一步领会基本概念。4.实例应用,结论拓展:教师活动:展示太空舱中宇航员的真实生活,引导学生应用本节所学知识予以解答。学生活动:小组讨论后形成共识。教师活动:(1)引导学生分小组回答相关问题,小组间互相完善补充,教师加以规范。(2)指定学生完成导学案中“思考与讨论二”的两个问题。
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题,经常需要应用正弦定理或余弦定理. 介绍 播放 课件 了解 观看 课件 学生自然的走向知识点 0 5*巩固知识 典型例题 例6一艘船以每小时36海里的速度向正北方向航行(如图1-14).在A处观察灯塔C在船的北偏东30°,0.5小时后船行驶到B处,再观察灯塔C在船的北偏东45°,求B处和灯塔C的距离(精确到0.1海里). 解 因为∠NBC=45°,A=30°,所以C=15°, AB = 36×0.5 = 18 (海里). 由正弦定理得 答:B处离灯塔约为34.8海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和B(图1-15),在平地上选择适合测量的点C,如果C=60°,AB = 350m,BC = 450m,试计算隧道AB的长度(精确到1m). 解 在△ABC中,由余弦定理知 =167500. 所以AB≈409m. 答:隧道AB的长度约为409m. 图1-15 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点 40

【高教版】中职数学拓展模块:3.2《二项式定理》教学设计
一、定义: ,这一公式表示的定理叫做二项式定理,其中公式右边的多项式叫做的二项展开式;上述二项展开式中各项的系数 叫做二项式系数,第项叫做二项展开式的通项,用表示;叫做二项展开式的通项公式.二、二项展开式的特点与功能1. 二项展开式的特点项数:二项展开式共(二项式的指数+1)项;指数:二项展开式各项的第一字母依次降幂(其幂指数等于相应二项式系数的下标与上标的差),第二字母依次升幂(其幂指数等于二项式系数的上标),并且每一项中两个字母的系数之和均等于二项式的指数;系数:各项的二项式系数下标等于二项式指数;上标等于该项的项数减去1(或等于第二字母的幂指数;2. 二项展开式的功能注意到二项展开式的各项均含有不同的组合数,若赋予a,b不同的取值,则二项式展开式演变成一个组合恒等式.因此,揭示二项式定理的恒等式为组合恒等式的“母函数”,它是解决组合多项式问题的原始依据.又注意到在的二项展开式中,若将各项中组合数以外的因子视为这一组合数的系数,则易见展开式中各组合数的系数依次成等比数列.因此,解决组合数的系数依次成等比数列的求值或证明问题,二项式公式也是不可或缺的理论依据.

【高教版】中职数学拓展模块:3.3《离散型随机变量及其分布》教学设计
重点分析:本节课的重点是离散型随机变量的概率分布,难点是理解离散型随机变量的概念. 离散型随机变量 突破难点的方法: 函数的自变量 随机变量 连续型随机变量 函数可以列表 X123456p 2 4 6 8 10 12
人教A版高中数学必修二平面与平面垂直教学设计
6. 例二:如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小. 解:由已知PA⊥平面ABC,BC在平面ABC内∴PA⊥BC∵AB是⊙O的直径,且点C在圆周上,∴AC⊥BC又∵PA∩AC=A,PA,AC在平面PAC内,∴BC⊥平面PAC又PC在平面PAC内,∴PC⊥BC又∵BC是二面角P-BC-A的棱,∴∠PCA是二面角P-BC-A的平面角由PA=AC知△PAC是等腰直角三角形∴∠PCA=45°,即二面角P-BC-A的大小是45°7.面面垂直定义一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直,平面α与β垂直,记作α⊥β8. 探究:建筑工人在砌墙时,常用铅锤来检测所砌的墙面与地面是否垂直,如果系有铅锤的细绳紧贴墙面,工人师傅被认为墙面垂直于地面,否则他就认为墙面不垂直于地面,这种方法说明了什么道理?

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
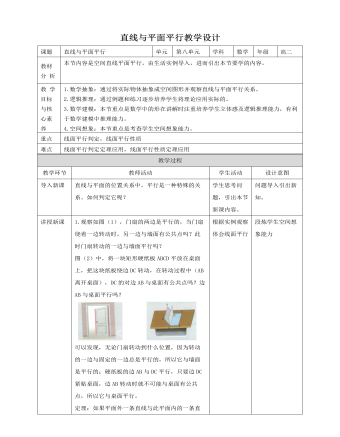
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。
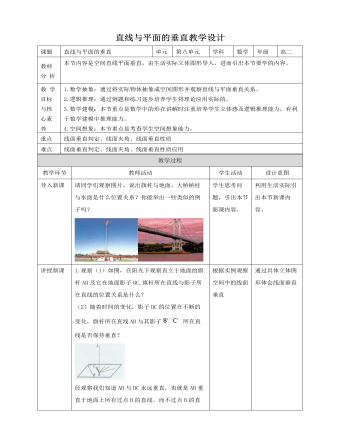
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=
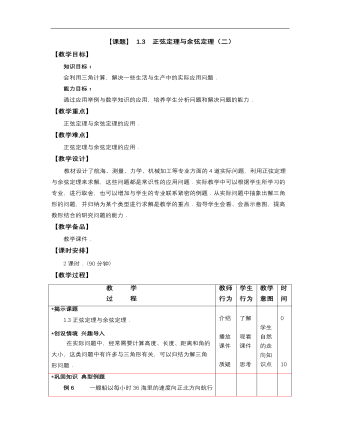
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点

【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 我们知道,在直角三角形(如图)中,,,即 ,, 由于,所以,于是 . 图1-6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中,是否也存在类似的数量关系呢? c 图1-7 当三角形为钝角三角形时,不妨设角为钝角,如图所示,以为原点,以射线的方向为轴正方向,建立直角坐标系,则 两边取与单位向量的数量积,得 由于设与角A,B,C相对应的边长分别为a,b,c,故 即 所以 同理可得 即 当三角形为锐角三角形时,同样可以得到这个结论.于是得到正弦定理: 在三角形中,各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题: (1)已知三角形的两个角和任意一边,求其他两边和一角. (2)已知三角形的两边和其中一边所对角,求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20

大班数学活动以客体为中心区分左右课件教案
2在以自身为中心区分左右的基础上,学会以客体为中心区分左右3培养幼儿的空间方位感,提高思维的灵活性二活动准备木偶,图示三活动过程(一)通过游戏,幼儿复习以自我为中心区分左右师:今天我们要玩一个游戏,当我说左手你们就伸出你们的左手,当我说右耳朵的时候你们就用手指着你们的右耳朵

人教版高中地理必修1山岳的形成教案
【转折过渡】除了以上所说的褶皱山和断层山之 外,是否还有其他类型的山脉呢?试举一例说明。【学生思考后回答】有,如富士山属于火山。【教师总结】同学们回答的很好,还有火山,那么火山是如何形成的呢?这就是我们要研究的下一个问题。【板书】3、火山【指导读书】请同学们阅读教材P81思考:①玄武岩高原和火山有什么联系与区别? ②火山由哪几部分构成的?③火山的规模是否相同?【学生回答】①联系:玄武岩高原和火山都是由于处于地下深处的岩浆,在巨大的压力作用下,有时候会沿着地壳的薄弱地带喷出地表而形成的。区别:玄武岩高原是岩浆沿着地壳的线状裂隙流出,往往比较宽广。如哥伦比亚高原。火山是岩浆沿着地壳的中央喷出口或管道喷出。如我国长白山的主峰。②火山由火山口和火山锥两部分组成。③火山的规模大小不一,大火山的相对高度可达4 000~5 000米,火山口直径为数百米;小火山的相对高度不及100米。

人教版高中地理选修2荒漠化的成因与防治教案
1、图4.10“西北地区土地荒漠化的人为因素(以风力作用为例)图”产生荒漠化的人为因素有过度农垦、过度放牧、过度樵采和不合理利用水资源等。从荒漠化和人类的关系来看,荒漠化的发生、发展和社会经济有着密切的联系,人类不合理的经济活动不仅是荒漠化发生的主要原因和活跃因素,同时人类又是它的直接受害者。2、图4.14“荒漠植物的生态适应图”荒漠植物的生态适应特征表现在:a类为肉质植物,体内薄壁组织可储存大量水分,其近地表分布的根系可以在偶然而短暂的降水过程(如暴雨)中收集水分;b类植物一方面利用其近地表根系吸收可能的降水,另一方面根系向纵深发展,以利用稳定的地下水;c类为微叶或无叶型植物,叶片强烈缩小或退化,由绿色叶茎行使光合作用功能,蒸腾很弱。【教学内容】一、荒漠化的成因1.荒漠化的自然原因荒漠化的自然原因包括干旱(基本条件)、地表物质松散(物质基础)和大风吹扬(动力因素)。

幼儿园中班上学期数学《按规律排列》优质课教案公开课教案比赛获奖教案
一、出示有规律排序的图像,复习找规律。 1、出示图像,幼儿分析。 师:朱老师在家画了两条彩带花纹,我想请小朋友看看,它们漂亮吗? 花纹是什么形状组成的呢?有什么颜色?你发现有什么规律吗? 2、请幼儿大胆说出规律:花纹是由黄色、蓝色、绿色的规律做成的。 3、教师再出示另一条彩带花纹。

少先队活动课 说课稿3篇
一、活动背景: 日照这座城市对于生长于此的同学来说并不陌生,可是孩子们对于自己的家乡的知识却是零散的,片面的。如果对家乡都没有一个系统全面的认识了解,又怎么谈得上热爱呢?根据《少先队活动课指导纲要》的要求,结合三年级少先队员的特点,决定开展以“知我日照,爱我家乡”为主题的中队会。 二、活动目标: 1、认识祖国的版图,了解家乡在祖国的地理位置。 2、了解家乡的风景名胜和丰富物产。 3、增强热爱家乡和热爱祖国的感情。 4、引发学生珍惜感恩现在身边来之不易的美好生活。 三、活动准备: 为了确保活动的成功举行,队会前做好充分的准备: 1、布置队员搜集整理资料,制作道具。 2、辅导员老师根据队员搜集的资料制作多媒体课件。 四、设计理念: 为保证每个队员积极参与,培养队员们的各项能力,本次活动主要采用各小队成果汇报的形式来进行,队员以小队为单位,依据自己的主题,分工合作,进行调查搜集等,以不同的展示方式汇报。

