-
中班体育教案：向手挑战
活动准备： 一段节奏明快活泼的音乐。 活动过程：1、我会做。 教师用手指着头部说：“这是我的头，你能摸到自己的头吗?”引导幼儿边用手指头部边说：“这是我的头。” 教师手指其他人体部位，提出类似问题。 引导幼儿闭眼做类似游戏，如用手摸肩，用手碰背等。
《学雷锋-争做向上向善好少年》主题班会说课稿
活动三——读《雷锋日记》让学生读雷锋给一位陌生老人送完手套后写的日记。重点理解“一路上，我的手虽冻得像针扎一样，心中却有一种说不出的愉快。”这一句话。让学生谈谈自己的感受。（此活动的目的是让学生了解雷锋的内心世界，理解雷锋精神的实质，全心合意为人民服务。)（三）讨论交流新时代还需要不需要学习雷锋?（1）小组讨论雷锋精神是不是已经过时了?新时代还用学雷锋吗?通过小组的讨论让学生认识雷锋精神的重要性，这是本次班会的重点内容，要引导学生积极参与，达到真正的思想教育。通过辩论后利用课件为学生们出示新时代的雷锋，《小林浩救人事迹》、感受社会的正能量。（设计本活动是让学生在讨论和辩论引起学生思想和情感的升华，更加深入理解雷锋精神对社会的重要性。)
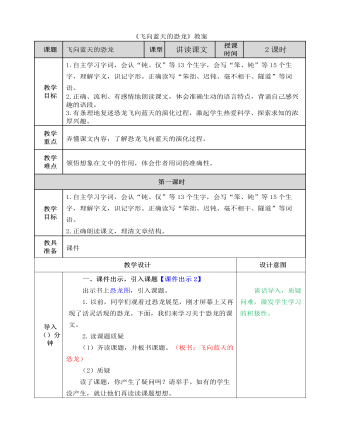
部编人教版四年级下册《 飞向蓝天的恐龙》教案
一、复习检查，导入新课师：上节课我们初步学习了这篇课文，知道了说明性文章表达准确的这一特点，今天我们继续来学习。首先，我们复习一下上节课学习过的词语，【课件出示17】出示词语：迟钝不仅描绘隧道繁衍十吨公斤脑颅膨大敏捷树栖开辟崭新笨重谈起鸽子毫不相关描绘末期形态各异前肢鸟翼师：这些词语都是第一自然段中，你们能用上这些词语概括出第一自然段的主要内容吗？【课件出示18】预设：（事实证明笨重的恐龙的一支经过漫长的演化，最终变成了凌空翱翔的鸟儿）。师：我们接下来学习课文，跟着科学家走进恐龙的演变世界。
部编人教版四年级下册《 飞向蓝天的恐龙》创新教案
【教学理念】 1.整体感知课文内容，理清文章思路。2.培养学生筛选信息能力，了解纳米的有关知识和应用前景。3.激发科学兴趣，培养学生勇于大胆想象的科学精神。【教学流程】一、谈话引入，激发兴趣。1．今天我们来学习一篇新课文《纳米技术就在我们身边》（板书课题）。2．以前听说过“纳米技术”吗？你了解纳米技术吗？是怎么了解到的？预设：我通过预习课文了解到“纳米技术”就是研究小小物质新奇特性的一门学问。预设：我是通过查找资料了解什么是纳米，什么是纳米技术的。二、通读课文，了解大意。1.检查课文朗读。出示课文中的科技术语和句子。先组内相互听读纠正，然后全班交流。词语：除臭技术纳米缓释技术长度单位纳米涂层碳纳米管纳米吸波材料探测雷达波。句子：纳米技术就是研究并利用这些特性造福于人类的一门新学问。2．自由交流：读了课文，你知道了什么？3.自学了课文后你有什么问题想问？
《战胜挫折 走向成功》主题班会教案
B、郑智化坐在轮椅上演唱自己作词作曲的歌《水手》。[多媒体播放郑智化唱《水手》一歌画面和音乐]①郑智化一上场为什么马上会赢得掌声？《水手》这首歌反映了郑智化怎样的思想境界？（引导学生谈郑智化的人生经历）由于郑智化的努力，“风雨中这点痛算什么”，经过思考斗争，使得悲观消极的情绪转化为奋斗有为、争取上进的积极情绪和心态。3、举出名人对待挫折的事例。（学生事先搜集，这里讲述梗概）司马迁在屈辱中完成了《史记》 屈原在流放期间写出《离骚》 曹雪芹在穷困潦倒中写出巨著《红楼梦》吴敬梓在贫困的寒夜写出了《儒林外史》……4、学生结合录相和故事，谈谈应该怎样正视挫折。[多媒体显示：怎样正视挫折]①要明白挫折是任何人都避免不了的，具有普遍、客观性。面对挫折时，要通过坚强的意志战胜自己的消沉和软弱，通过自己的努力，最终坚定地走向成功。[多媒体显示：挫折不可避免，通过坚强意志战胜]
空间向量基本定理教学设计人教A版高中数学选择性必修第一册
反思感悟用基底表示空间向量的解题策略1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.例2.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG=1/3 CD(1)证明:EF⊥B1C;(2)求EF与C1G所成角的余弦值.思路分析选择一个空间基底,将(EF) ?,(B_1 C) ?,(C_1 G) ?用基向量表示.(1)证明(EF) ?·(B_1 C) ?=0即可;(2)求(EF) ?与(C_1 G) ?夹角的余弦值即可.(1)证明:设(DA) ?=i,(DC) ?=j,(DD_1 ) ?=k,则{i,j,k}构成空间的一个正交基底.
人教版新课标小学数学三年级下册位置与方向教案2篇
【教学目标】1、知识目标：结合具体情境，使学生认识东、南、西、北四个方向，能够用给定的一个方向辨认其余的三个方向，并能用这些词语描述物体所在的方位。2、能力目标：培养学生良好的观察能力和空间想象能力。3、情感目标：体验数学与现实生活的密切关系，增强学生学数学、用数学的意识。【教学重难点】使学生认识东、南、西、北四个方向，并能根据学生自身的方位辨认东、南、西、北这四个方向。【教学准备】1、挂图、指南针2、学具准备:准备主题图中相关的学具卡片或实物。【教学过程】一、创设情境，引入新知：同学们，你们想去北京吗？今天我们去参观参观吧？二、愉快体验，探究新知1、认识方向：出示主题图：我们来到了北京的天安门广场，你们看见了哪些建筑物？愿意当小导游为大家介绍一个吗？（先同桌之间互相练习解说，师出示教学挂图，介绍天安门的地理位置）引出例1）
北师大初中七年级数学上册科学记数法教案1
解析：水是生命之源，节约水资源是我们每个居民都应有的意识.题中给出假如每人浪费一点水，当人数增多时，将是一个非常惊人的数字，100万人每天浪费的水资源为1000000×0.32＝320000（升）.所以320000＝3.2×105.故选B.方法总结：从实际问题入手让学生体会科学记数法的实际应用.题中没有直接给出数据，应先计算，再表示.探究点二：将用科学记数法表示的数转换为原数已知下列用科学记数法表示的数，写出原来的数：（1）2.01×104；（2）6.070×105.解析：（1）将2.01的小数点向右移动4位即可；（2）将6.070的小数点向右移动5位即可.解：（1）2.01×104＝20100；（2）6.070×105＝607000.方法总结：将科学记数法a×10n表示的数，“还原”成通常表示的数，就是把a的小数点向右移动n位所得到的数.三、板书设计借助身边熟悉的事物进一步体会大数，积累数学活动经验，发展数感、空间感，培养学生自主学习的能力.
北师大初中七年级数学上册科学记数法教案2
光年是表示较大距离的一个单位, 而纳米(nanometer)则是表示微小距离的单位。1纳米= 米，即1米= 纳米。我们通常使用的尺上的一小格是一毫米(mm)，1毫米= 米。可见，1毫米= 纳米，容易算出，1纳米相当于1毫米的一百万分之一。可想而知，1纳米是多么的小。超微粒子的大小一般在1～100 纳米范围内，故又称纳米粒子。纳米粒子的尺寸小，表面积大，具有高度的活性。因此，利用纳米粒子可制备活性极高的催化剂，在火箭固体燃料中掺入铝的纳米微粒，可提高燃烧效率若干倍。利用铁磁纳米材料具有很高矫顽力的特点，可制成磁性信用卡、磁性钥匙，以及高性能录像带等 。利用纳米材料等离子共振频率的可调性可制成隐形飞机的涂料。纳米材料的表面积大，对外界环境(物理的和化学的)十分敏感，在制造传感器方面是有前途的材料，目前已开发出测量温度、热辐射和检测各种特定气体的传感器。在生物和医学中也有重要应用。纳米材料科学是20世纪80年代末诞生并正在崛起的科技新领域，它将成为跨世纪的科技热点之一。
部编人教版四年级下册《 飞向蓝天的恐龙》说课稿
二、精读重点段，理解演化过程接下来我直奔重点-——课文的第3、4自然段。我以“让我们穿越时空隧道，一起去中生代的地球，看看恐龙的演化过程”这一陈述，十分自然地引出后面的学习。在学习中，我紧紧围绕“恐龙是如何飞向蓝天的”这一问题，设计了合作学习表格，教给学生抓关键词来填表格的方法，引导学生边读边思考，学会学习，学生在完成表格的过程中，不仅理清了课文的叙述顺序，也清楚地知道了恐龙飞向蓝天的过程。有了表格的提示，学生们把课文梳理得更清楚简洁。我又通过填空，图片解说，以及不同形式的朗读进一步加深印象。学生通过自主的，入情入境的朗读，读懂了课文。读的要求明确，读的时间充足，读的层次清楚，使学生亲历阅读过程，走进文本。
人教版新课标高中物理必修2向心力教案2篇
3．进一步体会力是产生加速度的原因，并通过牛顿第二定律来理解匀速圆周运动、变速圆周运动及一般曲线运动的各自特点。（三）、情感、态度与价值观1．在实验中，培养学生动手、探究的习惯。2．体会实验的意义，感受成功的快乐，激发学生探究问题的热情、乐于学习的品质。教学重点1．体会牛顿第二定律在向心力上的应用。2．明确向心力的意义、作用、公式及其变形，并经行计算。教学难点1．对向心力的理解及来源的寻找。2．运用向心力、向心加速度的知识解决圆周运动问题。教学过程（一）、 引入新课：复习提问：匀速圆周运动的物体的加速度——向心加速度，它的方向和大小有何特点呢？学生回答后进一步引导：那做匀速圆周运动物体的受力有什么特点呢？是什么力使物体做圆周运动而不沿直线飞出？请同学们先阅读教材
第十七周国旗下讲话稿：拒绝雾霾 向PM2.5说“不”
第十七周国旗下讲话稿：拒绝雾霾向Pm2.5说“不”近些年来，“雾霾”这一个词逐渐被人们常常提及，从北方到南方，全国各地都不同程度地出现了影响我们正常的生活的雾霾天。那什么是雾霾呢？雾霾又会给我们带来什么样的危害呢？霾，雾和霾的统称。也是我们众所周知的Pm2.5。“Pm2.5”很细小，肉眼看不到。打个比方，人类头发已经很细了，而头发却比最大的Pm2.5还大了近三十倍。可别看Pm2.5的颗粒径小，却能吸附大量的有毒、有害物质，而且它们能在大气中停留更长时间，对同学们的呼吸系统，心脑血管的影响较大。远离雾霾天气，需要我们低碳生活。怎样才是低碳生活？.绿色出行，动员家长少开私家车，选择公交车出行或步行、骑自行车，减少汽车尾气的排放，让大自然有更清新的空气。
幼儿园大班美术教案：七彩蛇
活动准备： ⒈活动前幼儿玩过用手臂来模仿蛇的游戏； ⒉幼儿自带用做蛇的眼睛的材料（如：小瓶盖、纸团、彩色玻璃球等）； ⒊活动室中布置一些较高大的绿色植物，营造森林的氛围；数码相机； ⒋创作材料：脸彩棒人手一份。 活动过程： 1、游戏导入：师生共同用手臂来玩蛇游动的游戏，引起幼儿的活动兴趣。 和幼儿一起回忆看过的蛇身上的花纹，请他们谈谈自己的感受，帮助幼儿充分感知色彩美和图案美，为创作活动奠定基础。 激发创作热情：“你这条蛇漂亮吗？为什么？怎样让它也漂亮起来？”
用空间向量研究距离、夹角问题（1）教学设计人教A版高中数学选择性必修第一册
二、探究新知一、点到直线的距离、两条平行直线之间的距离1.点到直线的距离已知直线l的单位方向向量为μ,A是直线l上的定点,P是直线l外一点.设(AP) ?=a,则向量(AP) ?在直线l上的投影向量(AQ) ?=(a·μ)μ.点P到直线l的距离为PQ=√(a^2 "-(" a"·" μ")" ^2 ).2.两条平行直线之间的距离求两条平行直线l,m之间的距离,可在其中一条直线l上任取一点P,则两条平行直线间的距离就等于点P到直线m的距离.点睛：点到直线的距离,即点到直线的垂线段的长度,由于直线与直线外一点确定一个平面,所以空间点到直线的距离问题可转化为空间某一个平面内点到直线的距离问题.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是C1C,D1A1的中点,则点A到直线EF的距离为 . 答案: √174/6解析:如图,以点D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(2,0,0),E(0,2,1),F(1,0,2),(EF) ?=(1,-2,1),
用空间向量研究直线、平面的位置关系（2）教学设计人教A版高中数学选择性必修第一册
跟踪训练1在正方体ABCD-A1B1C1D1中,E为AC的中点.求证:(1)BD1⊥AC;(2)BD1⊥EB1.(2)∵(BD_1 ) ?=(-1,-1,1),(EB_1 ) ?=(1/2 "," 1/2 "," 1),∴(BD_1 ) ?·(EB_1 ) ?=(-1)×1/2+(-1)×1/2+1×1=0,∴(BD_1 ) ?⊥(EB_1 ) ?,∴BD1⊥EB1.证明:以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系.设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E(1/2 "," 1/2 "," 0),B1(1,1,1).(1)∵(BD_1 ) ?=(-1,-1,1),(AC) ?=(-1,1,0),∴(BD_1 ) ?·(AC) ?=(-1)×(-1)+(-1)×1+1×0=0.∴(BD_1 ) ?⊥(AC) ?,∴BD1⊥AC.例2在棱长为1的正方体ABCD-A1B1C1D1中,E,F,M分别为棱AB,BC,B1B的中点.求证:D1M⊥平面EFB1.思路分析一种思路是不建系,利用基向量法证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直,从而根据线面垂直的判定定理证得结论;另一种思路是建立空间直角坐标系,通过坐标运算证明(D_1 M) ?与平面EFB1内的两个不共线向量都垂直;还可以在建系的前提下,求得平面EFB1的法向量,然后说明(D_1 M) ?与法向量共线,从而证得结论.证明:(方法1)因为E,F,M分别为棱AB,BC,B1B的中点,所以(D_1 M) ?=(D_1 B_1 ) ?+(B_1 M) ?=(DA) ?+(DC) ?+1/2 (B_1 B) ?,而(B_1 E) ?=(B_1 B) ?+(BE) ?=(B_1 B) ?-1/2 (DC) ?,于是(D_1 M) ?·(B_1 E) ?=((DA) ?+(DC) ?+1/2 (B_1 B) ?)·((B_1 B) ?-1/2 (DC) ?)=0-0+0-1/2+1/2-1/4×0=0,因此(D_1 M) ?⊥(B_1 E) ?.同理(D_1 M) ?⊥(B_1 F) ?,又因为(B_1 E) ?,(B_1 F) ?不共线,因此D1M⊥平面EFB1.
空间向量及其运算的坐标表示教学设计人教A版高中数学选择性必修第一册
一、情境导学我国著名数学家吴文俊先生在《数学教育现代化问题》中指出:“数学研究数量关系与空间形式,简单讲就是形与数,欧几里得几何体系的特点是排除了数量关系,对于研究空间形式,你要真正的‘腾飞’,不通过数量关系,我想不出有什么好的办法…….”吴文俊先生明确地指出中学几何的“腾飞”是“数量化”,也就是坐标系的引入,使得几何问题“代数化”,为了使得空间几何“代数化”,我们引入了坐标及其运算.二、探究新知一、空间直角坐标系与坐标表示1.空间直角坐标系在空间选定一点O和一个单位正交基底{i,j,k},以点O为原点,分别以i,j,k的方向为正方向、以它们的长为单位长度建立三条数轴:x轴、y轴、z轴,它们都叫做坐标轴.这时我们就建立了一个空间直角坐标系Oxyz,O叫做原点,i,j,k都叫做坐标向量,通过每两个坐标轴的平面叫做坐标平面,分别称为Oxy平面,Oyz平面,Ozx平面.
用空间向量研究直线、平面的位置关系（1）教学设计人教A版高中数学选择性必修第一册
二、探究新知一、空间中点、直线和平面的向量表示1.点的位置向量在空间中,我们取一定点O作为基点,那么空间中任意一点P就可以用向量(OP) ?来表示.我们把向量(OP) ?称为点P的位置向量.如图.2.空间直线的向量表示式如图①,a是直线l的方向向量,在直线l上取(AB) ?=a,设P是直线l上的任意一点,则点P在直线l上的充要条件是存在实数t,使得(AP) ?=ta,即(AP) ?=t(AB) ?.如图②,取定空间中的任意一点O,可以得到点P在直线l上的充要条件是存在实数t,使(OP) ?=(OA) ?+ta, ①或(OP) ?=(OA) ?+t(AB) ?. ②①式和②式都称为空间直线的向量表示式.由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.1.下列说法中正确的是( )A.直线的方向向量是唯一的B.与一个平面的法向量共线的非零向量都是该平面的法向量C.直线的方向向量有两个D.平面的法向量是唯一的答案:B 解析:由平面法向量的定义可知,B项正确.
飞向蓝天的恐龙（说课稿）
1.通过预习，让学生认识13个生字，会写15个生字，正确读写本课词语。2、正确流利有感情的朗读课文。3、有条理的复述恐龙飞向蓝天的演化过程。过程与方法：通过反复读课文，运用小组合作学习，了解恐龙飞向蓝天的演化过程。情感态度与价值观：激起学生热爱科学、探索求知的浓厚兴趣。教学重点：引导学生体会恐龙演化的过程教学难点：引导学生体会课文语言准确生动的表达特点。【说教法】“教有多法，但无定法。”在本课中主要采用情景教学法、多媒体辅助法和小组合作法进行教学。通过展示课件让学生身临其境，情寓其中，从而激起热爱科学、探索求知的浓厚兴趣，并让学生在读中感悟、品味，更好地理解课文。
人教部编版七年级下册孙权劝学教案
（所有扮演吕蒙的学生举手，老师任选学生回答问题）预设 ①多读书能拓宽视野，丰富知识。②自己先天基础差，能力不足，就要靠后天的努力学习来争取进步。③用心听取别人的建议，并努力去做到最好。师小结：感谢三位接受我的采访！吕蒙先生的话让老师想起了冰心的名言：读书好，好读书，读好书。同学们，让我们与书籍同行，打好人生的基础；让我们以博览为志，拓宽视野。“腹有诗书气自华。” “问渠那得清如许？为有源头活水来。”愿同学们在知识的海洋里乘风破浪，扬帆远航！【设计意图】本环节采用记者采访的活动形式，由课内延伸至课外，最大限度地激发学生学习的兴趣。学生在活动中，不仅可以探究文章主题，更能切身体会到学习的重要性。四、布置作业1.课后自己整理、积累相关的文学常识和文言词语。2.比较阅读。通过比较《孙权劝学》和《伤仲永》，深化对课文内容的理解。
部编版语文七年级下册《孙权劝学》教案
二、介绍故事出处和文中人物《资治通鉴》是司马光主持编纂的一部编年体通史，记载了从战国到五代共1362年间的史事。司马光：字君实，陕州夏县人，北宋政治家、史学家。书名“资治”，说明本书编撰的目的是为封建统治阶级提供政治借鉴。孙权（182—252）：字仲谋，吴郡富春人，三国时吴国的建立者。吕蒙：字子明，三国时吴国名将。三、朗读感知课文1、听朗读课文，注意人物对话的语气 （1）“卿今当涂掌事，不可不学！” 语重心长，谆谆告诫（2）“孤岂欲卿治经为博士邪！” （反问句，强调并不是要吕蒙研究儒家经典，当专掌经学传授的学官，而是有别的目的。）（3）“卿言多务，孰若孤？” 反问句，否定吕蒙辞以多务的理由。要重读强调（4）“卿今者才略，非复吴下阿蒙！” 感叹句，要显出惊讶不解的语气（5）“大兄何见事之晚乎！”反问句，指责中带有自豪的语气
