-

【高教版】中职数学拓展模块:3.3《离散型随机变量及其分布》教学设计
重点分析:本节课的重点是离散型随机变量的概率分布,难点是理解离散型随机变量的概念. 离散型随机变量 突破难点的方法: 函数的自变量 随机变量 连续型随机变量 函数可以列表 X123456p 2 4 6 8 10 12

高教版中职数学基础模块下册:10.1《计数原理》教学设计
授课 日期 班级16高造价 课题: §10.1 计数原理 教学目的要求: 1.掌握分类计数原理与分步计数原理的概念和区别; 2.能利用两个原理分析和解决一些简单的应用问题; 3.通过对一些应用问题的分析,培养自己的归纳概括和逻辑判断能力. 教学重点、难点: 两个原理的概念与区别 授课方法: 任务驱动法 小组合作学习法 教学参考及教具(含多媒体教学设备): 《单招教学大纲》、课件 授课执行情况及分析: 板书设计或授课提纲 §10.1 计数原理 1、加法原理 2、乘法原理 3、两个原理的区别
高教版中职数学基础模块下册:10.2《概率》教学设计
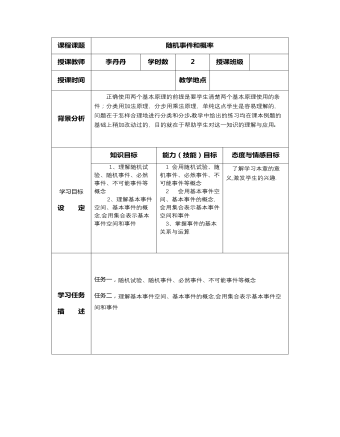
课程课题随机事件和概率授课教师李丹丹学时数2授课班级 授课时间 教学地点 背景分析正确使用两个基本原理的前提是要学生清楚两个基本原理使用的条件;分类用加法原理,分步用乘法原理,单纯这点学生是容易理解的,问题在于怎样合理地进行分类和分步教学中给出的练习均在课本例题的基础上稍加改动过的,目的就在于帮助学生对这一知识的理解与应用 学习目标 设 定知识目标能力(技能)目标态度与情感目标1、理解随机试验、随机事件、必然事件、不可能事件等概念 2、理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件 1 会用随机试验、随机事件、必然事件、不可能事件等概念 2 会用基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件 3、掌握事件的基本关系与运算 了解学习本章的意义,激发学生的兴趣. 学习任务 描 述 任务一,随机试验、随机事件、必然事件、不可能事件等概念 任务二,理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件

高教版中职数学基础模块下册:10.3《总体、样本与抽样方法》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 10.3总体、样本与抽样方法(一) *创设情境 兴趣导入 【实验】 商店进了一批苹果,小王从中任意选取了10个苹果,编上号并称出质量.得到下面的数据(如表10-6所示): 苹果编号12345678910质量(kg)0.210.170.190.160.200.220.210.180.190.17 利用这些数据,就可以估计出这批苹果的平均质量及苹果的大小是否均匀. 介绍 质疑 讲解 说明 了解 思考 启发 学生思考 0 10*动脑思考 探索新知 【新知识】 在统计中,所研究对象的全体叫做总体,组成总体的每个对象叫做个体. 上面的实验中,这批苹果的质量是研究对象的总体,每个苹果的质量是研究的个体. 讲解 说明 引领 分析 理解 记忆 带领 学生 分析 20*巩固知识 典型例题 【知识巩固】 例1 研究某班学生上学期数学期末考试成绩,指出其中的总体与个体. 解 该班所有学生的数学期末考试成绩是总体,每一个学生的数学期末考试成绩是个体. 【试一试】 我们经常用灯泡的使用寿命来衡量灯炮的质量.指出在鉴定一批灯泡的质量中的总体与个体. 说明 强调 引领 观察 思考 主动 求解 通过例题进一步领会 35

高教版中职数学基础模块下册:10.4《用样本估计总体》教学设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 10.4 用样本估计总体 *创设情境 兴趣导入 【知识回顾】 初中我们曾经学习过频数分布图和频数分布表,利用它们可以清楚地看到数据分布在各个组内的个数. 【知识巩固】 例1 某工厂从去年全年生产某种零件的日产记录(件)中随机抽取30份,得到以下数据: 346 345 347 357 349 352 341 345 358 350 354 344 346 342 345 358 348 345 346 357 350 345 352 349 346 356 351 355 352 348 列出频率分布表. 解 分析样本的数据.其最大值是358,最小值是341,它们的差是358-341=17.取组距为3,确定分点,将数据分为6组. 列出频数分布表 【小提示】 设定分点数值时需要考虑分点值不要与样本数据重合. 分 组频 数 累 计频 数340.5~343.5┬2343.5~346.5正 正10346.5~349.5正5349.5~352.5正  ̄6352.5~355.5┬2355.5~358.5正5合 计3030 介绍 质疑 引领 分析 讲解 说明 了解 观察 思考 解答 启发 学生思考 0 10*动脑思考 探索新知 【新知识】 各组内数据的个数,叫做该组的频数.每组的频数与全体数据的个数之比叫做该组的频率. 计算上面频数分布表中各组的频率,得到频率分布表如表10-8所示. 表10-8 分 组频 数频 率340.5~343.520.067343.5~346.5100.333346.5~349.550.167349.5~352.560.2352.5~355.520.067355.5~358.550.166合 计301.000 根据频率分布表,可以画出频率分布直方图(如图10-4). 图10-4 频率分布直方图的横轴表示数据分组情况,以组距为单位;纵轴表示频率与组距之比.因此,某一组距的频率数值上等于对应矩形的面积. 【想一想】 各小矩形的面积之和应该等于1.为什么呢? 【新知识】 图10-4显示,日产量为344~346件的天数最多,其频率等于该矩形的面积,即 . 根据样本的数据,可以推测,去年的生产这种零件情况:去年约有的天数日产量为344~346件. 频率分布直方图可以直观地反映样本数据的分布情况.由此可以推断和估计总体中某事件发生的概率.样本选择得恰当,这种估计是比较可信的. 如上所述,用样本的频率分布估计总体的步骤为: (1) 选择恰当的抽样方法得到样本数据; (2) 计算数据最大值和最小值、确定组距和组数,确定分点并列出频率分布表; (3) 绘制频率分布直方图; (4) 观察频率分布表与频率分布直方图,根据样本的频率分布,估计总体中某事件发生的概率. 【软件链接】 利用与教材配套的软件(也可以使用其他软件),可以方便的绘制样本数据的频率分布直方图,如图10-5所示. 图10?5 讲解 说明 引领 分析 仔细 分析 关键 语句 观察 理解 记忆 带领 学生 分析 25

冬季安全教育国旗下讲话稿:冬季安全知识教育
尊敬的老师、亲爱的同学们:早上好!今天我在国旗下讲话的题目是《冬季安全知识教育》。天气渐渐寒冷,冰霜雪雾,恶劣的天气必将会给我们的学习和生活带来诸多不便和安全隐患,因此,多了解一些冬季安全知识,尤为重要。为确保校园安全和师生安全,学校对全体同学特进行冬季安全知识教育,请同学们谨记于心,并且遵照执行。一、冬季注意交通安全冬天寒风凛冽,雪花飘飘。地面上结起了一层冰,道路又湿又滑,很容易摔跤,同学们上下学行走时一定不能急奔快跑。不能在道路上堆雪人、打雪仗和滚雪球,这样既不安全,又会影响交通,甚至发生车祸。根据国家规定,学校严禁小学生骑自行车上学,尤其在冬天,道路结冰,骑车很容易造成打滑摔跤,甚至造成交通事故,因此为了自身安全,全体同学应该遵照学校要求,不坐无证、无牌、报废车辆。上、放学路上,一定要注意交通安全,雨雪天道路路况很差,车辆的制动效果不好,司机视线也差,同学们要严格遵守交通规则,过马路时要密切关注来往车辆,不要抢红灯。此外,有的同学由于天气寒冷戴上了帽子和口罩,请大家可千万不要遮住了自己的眼睛,以免影响视线而造成交通事故的发生。

XX年秋安全教育国旗下讲话稿:加强安全教育 增强防范意识
XX年秋安全教育国旗下讲话稿:加强安全教育增强防范意识老师、同学们:上午好!今天,我讲话的题目是《加强安全教育,增强防范意识》。校园安全与我们大家密切相关,它关系到同学们能否健康成长,能否顺利地完成学业;也关系到我们的老师能否在一个安全的环境中教书育人。我们必须清醒地认识到“安全无小事”。为进一步做好我校的安全教育工作,现提出以下十点要求,希望全体同学认真做好。1、要时刻保持高度的安全意识。认真学习相关的安全自护、自救知识,切实提高自我防护能力。2、要注意课间休息文明。不大声喧哗,不追赶打闹,出进教室不奔跑,不嬉戏,不在教室门口、走廊玩耍。上下楼梯注意楼道安全。3、要注意运动安全。上体育课前要作好准备活动,运动时要遵照体育老师的要求,不剧烈碰撞,不违规运动。防止运动器材伤人。

新人教版高中英语选修2Unit 1 Science and Scientists-Discovering useful structures教学设计
The grammatical structure of this unit is predicative clause. Like object clause and subject clause, predicative clause is one of Nominal Clauses. The leading words of predicative clauses are that, what, how, what, where, as if, because, etc.The design of teaching activities aims to guide students to perceive the structural features of predicative clauses and think about their ideographic functions. Beyond that, students should be guided to use this grammar in the context apporpriately and flexibly.1. Enable the Ss to master the usage of the predicative clauses in this unit.2. Enable the Ss to use the predicative patterns flexibly.3. Train the Ss to apply some skills by doing the relevant exercises.1.Guide students to perceive the structural features of predicative clauses and think about their ideographic functions.2.Strengthen students' ability of using predicative clauses in context, but also cultivate their ability of text analysis and logical reasoning competence.Step1: Underline all the examples in the reading passage, where noun clauses are used as the predicative. Then state their meaning and functions.1) One theory was that bad air caused the disease.2) Another theory was that cholera was caused by an infection from germs in food or water.3) The truth was that the water from the Broad Street had been infected by waste.Sum up the rules of grammar:1. 以上黑体部分在句中作表语。2. 句1、2、3中的that在从句中不作成分,只起连接作用。 Step2: Review the basic components of predicative clauses1.Definition

新人教版高中英语选修2Unit 4 Journey Across a Vast Land教学设计
当孩子们由父母陪同时,他们才被允许进入这个运动场。3.过去分词(短语)作状语时的几种特殊情况(1)过去分词(短语)在句中作时间、条件、原因、让步状语时,相当于对应的时间、条件、原因及让步状语从句。Seen from the top of the mountain (=When it is seen from the top of the mountain), the whole town looks more beautiful.从山顶上看,整个城市看起来更美了。Given ten more minutes (=If we are given ten more minutes), we will finish the work perfectly.如果多给十分钟,我们会完美地完成这项工作。Greatly touched by his words (=Because she was greatly touched by his words), she was full of tears.由于被他的话深深地感动,她满眼泪花。Warned of the storm (=Though they were warned of the storm), the farmers were still working on the farm.尽管被警告了风暴的到来,但农民们仍在农场干活。(2)过去分词(短语)在句中作伴随、方式等状语时,可改为句子的并列谓语或改为并列分句。The teacher came into the room, followed by two students (=and was followed by two students).后面跟着两个学生,老师走进了房间。He spent the whole afternoon, accompanied by his mom(=and was accompanied by his mom).他由母亲陪着度过了一整个下午。

新人教版高中英语选修2Unit 1 Science and Scientists-Learning about Language教学设计
Step 7: complete the discourse according to the grammar rules.Cholera used to be one of the most 1.__________ (fear) diseases in the world. In the early 19th century, _2_________ an outbreak of cholera hit Europe, millions of people died. But neither its cause, 3__________ its cure was understood. A British doctor, John Snow, wanted to solve the problem and he knew that cholera would not be controlled _4_________ its cause was found. In general, there were two contradictory theories 5 __________ explained how cholera spread. The first suggested that bad air caused the disease. The second was that cholera was caused by an _6_________(infect) from germs in food or water. John Snow thought that the second theory was correct but he needed proof. So when another outbreak of cholera hit London in 1854, he began to investigate. Later, with all the evidence he _7_________ (gather), John Snow was able to announce that the pump water carried cholera germs. Therefore, he had the handle of the pump _8_________ (remove) so that it couldn't be used. Through his intervention,the disease was stopped in its tracks. What is more, John Snow found that some companies sold water from the River Thames that __9__________________ (pollute) by raw waste. The people who drank this water were much more likely _10_________ (get) cholera than those who drank pure or boiled water. Through John Snow's efforts, the _11_________ (threaten) of cholera around the world saw a substantial increase. Keys: 1.feared 2.when 3. nor 4.unless 5.that/which 6.infection 7.had gathered 8.removed 9.was polluted 10.to get 11. threat

新人教版高中英语选修2Unit 1 Science and Scientists-Reading and thinking教学设计
Step 5: After learning the text, discuss with your peers about the following questions:1.John Snow believed Idea 2 was right. How did he finally prove it?2. Do you think John Snow would have solved this problem without the map?3. Cholera is a 19th century disease. What disease do you think is similar to cholera today?SARS and Covid-19 because they are both deadly and fatally infectious, have an unknown cause and need serious public health care to solve them urgently.keys:1. John Snow finally proved his idea because he found an outbreak that was clearly related to cholera, collected information and was able to tie cases outside the area to the polluted water.2. No. The map helped John Snow organize his ideas. He was able to identify those households that had had many deaths and check their water-drinking habits. He identified those houses that had had no deaths and surveyed their drinking habits. The evidence clearly pointed to the polluted water being the cause.3. SARS and Covid-19 because they are both deadly and fatally infectious, have an unknown cause and need serious public health care to solve them urgently.Step 6: Consolidate what you have learned by filling in the blanks:John Snow was a well-known _1___ in London in the _2__ century. He wanted to find the _3_____ of cholera in order to help people ___4_____ it. In 1854 when a cholera __5__ London, he began to gather information. He ___6__ on a map ___7___ all the dead people had lived and he found that many people who had ___8____ (drink) the dirty water from the __9____ died. So he decided that the polluted water ___10____ cholera. He suggested that the ___11__ of all water supplies should be _12______ and new methods of dealing with ____13___ water be found. Finally, “King Cholera” was __14_____.Keys: 1. doctor 2. 19th 3.cause 4.infected with 5.hit 6.marked 7.where 8.drunk 9.pump 10.carried 11.source 12.examined 13.polluted 14.defeatedHomework: Retell the text after class and preview its language points

新人教版高中英语选修2Unit 1 Science and Scientists-Using langauge教学设计
This happens because the dish soap molecules have a strong negative charge, and the milk molecules have a strong positive charge. Like magnets, these molecules are attracted to each other, and so they appear to move around on the plate, taking the food coloring with them, making it look like the colors are quickly moving to escape from the soap.Listening text:? Judy: Oh, I'm so sorry that you were ill and couldn't come with us on our field trip. How are you feeling now? Better?? Bill: Much better, thanks. But how was it?? Judy: Wonderful! I especially liked an area of the museum called Light Games.it was really cool. They had a hall of mirrors where I could see myself reflected thousands of times!? Bill: A hall of mirrors can be a lot of fun. What else did they have?? Judy: Well, they had an experiment where we looked at a blue screen for a while, and then suddenly we could see tiny bright lights moving around on it. You'll never guess what those bright lights were!? Bill: Come on, tell me!? Judy: They were our own blood cells. For some reason, our eyes play tricks on us when we look at a blue screen, and we can see our own blood cells moving around like little lights! But there was another thing I liked better. I stood in front of a white light, and it cast different shadows of me in every color of the rainbow!? Bill: Oh, I wish I had been there. Tell me more!? Judy: Well, they had another area for sound. They had a giant piano keyboard that you could use your feet to play. But then, instead of playing the sounds of a piano, it played the voices of classical singers! Then they had a giant dish, and when you spoke into it, it reflected the sound back and made it louder. You could use it to speak in a whisper to someone 17 meters away.? Bill: It all sounds so cool. I wish I could have gone with you? Judy: I know, but we can go together this weekend. I'd love to go there again!? Bill: That sounds like a great idea!

新人教版高中英语选修2Unit 2 Bridging Cultures-Discovering useful structures教学设计
The grammar of this unit is designed to review noun clauses. Sentences that use nouns in a sentence are called noun clauses. Nominal clauses can act as subject, object, predicate, appositive and other components in compound sentences. According to the above-mentioned different grammatical functions, nominal clauses are divided into subject clause, object clause, predicate clause and appositive clause. In this unit, we will review the three kinds of nominal clauses. Appositive clauses are not required to be mastered in the optional compulsory stage, so they are not involved.1. Guide the students to judge the compound sentences and determine the composition of the clauses in the sentence.2. Instruct students to try to learn grammar by generalizing grammar rules, controlling written practice, and semi-open oral output.3. Inspire the students to systematize the function and usage of noun clause1.Instruct students to try to learn grammar by generalizing grammar rules, controlling written practice, and semi-open oral output.2.Inspire the students to systematize the function and usage of noun clauseStep1: The teacher ask studetns to find out more nominal clauses from the reading passage and udnerline the nominal clauses.

新人教版高中英语选修2Unit 5 First Aid-Discovering useful structures教学设计
You have no excuse for not going.你没有理由不去。He was punished for not having finished his homework.他因未完成作业而受到惩罚。2.动词ing形式复合结构由物主代词或人称代词宾格、名词所有格或普通格加动词ing,即“sb./sb.'s+doing”构成。动词ing形式的复合结构实际上是给动词ing形式加了一个逻辑主语。动词ing形式的复合结构有四种形式:①形容词性物主代词+动词ing②名词所有格+动词ing③代词宾格+动词ing④名词+动词ingHer coming to help encouraged all of us.她来帮忙鼓舞了我们所有人。The baby was made awake by the door suddenly shutting.这个婴儿被突然的关门声吵醒了。Can you imagine him/Jack cooking at home?你能想象他/杰克在家做饭的样子吗?无生命名词无论是作主语还是作宾语都不能用第②种形式。Tom's winning first prize last year impressed me a lot.汤姆去年得了一等奖使我印象深刻。Do you mind my/me/Jack's/Jack leaving now?你介意我/杰克现在离开吗?Excuse me for my not coming on time.很抱歉我没能按时来。His father's being ill made him worried.他父亲病了,他很担心。We are looking forward to the singer's/the singer to give us a concert.我们盼望着这位歌手来给我们举办一场演唱会。

空间向量基本定理教学设计人教A版高中数学选择性必修第一册
反思感悟用基底表示空间向量的解题策略1.空间中,任一向量都可以用一个基底表示,且只要基底确定,则表示形式是唯一的.2.用基底表示空间向量时,一般要结合图形,运用向量加法、减法的平行四边形法则、三角形法则,以及数乘向量的运算法则,逐步向基向量过渡,直至全部用基向量表示.3.在空间几何体中选择基底时,通常选取公共起点最集中的向量或关系最明确的向量作为基底,例如,在正方体、长方体、平行六面体、四面体中,一般选用从同一顶点出发的三条棱所对应的向量作为基底.例2.在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是DD1,BD的中点,点G在棱CD上,且CG=1/3 CD(1)证明:EF⊥B1C;(2)求EF与C1G所成角的余弦值.思路分析选择一个空间基底,将(EF) ?,(B_1 C) ?,(C_1 G) ?用基向量表示.(1)证明(EF) ?·(B_1 C) ?=0即可;(2)求(EF) ?与(C_1 G) ?夹角的余弦值即可.(1)证明:设(DA) ?=i,(DC) ?=j,(DD_1 ) ?=k,则{i,j,k}构成空间的一个正交基底.

点到直线的距离公式教学设计人教A版高中数学选择性必修第一册
4.已知△ABC三个顶点坐标A(-1,3),B(-3,0),C(1,2),求△ABC的面积S.【解析】由直线方程的两点式得直线BC的方程为 = ,即x-2y+3=0,由两点间距离公式得|BC|= ,点A到BC的距离为d,即为BC边上的高,d= ,所以S= |BC|·d= ×2 × =4,即△ABC的面积为4.5.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.解:(方法一)∵点A(1,1)与B(-3,1)到y轴的距离不相等,∴直线l的斜率存在,设为k.又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.由点A(1,1)与B(-3,1)到直线l的距离相等,∴直线l的方程是y=2或x-y+2=0.得("|" k"-" 1+2"|" )/√(k^2+1)=("|-" 3k"-" 1+2"|" )/√(k^2+1),解得k=0或k=1.(方法二)当直线l过线段AB的中点时,A,B两点到直线l的距离相等.∵AB的中点是(-1,1),又直线l过点P(0,2),∴直线l的方程是x-y+2=0.当直线l∥AB时,A,B两点到直线l的距离相等.∵直线AB的斜率为0,∴直线l的斜率为0,∴直线l的方程为y=2.综上所述,满足条件的直线l的方程是x-y+2=0或y=2.

两点间的距离公式教学设计人教A版高中数学选择性必修第一册
一、情境导学在一条笔直的公路同侧有两个大型小区,现在计划在公路上某处建一个公交站点C,以方便居住在两个小区住户的出行.如何选址能使站点到两个小区的距离之和最小?二、探究新知问题1.在数轴上已知两点A、B,如何求A、B两点间的距离?提示:|AB|=|xA-xB|.问题2:在平面直角坐标系中能否利用数轴上两点间的距离求出任意两点间距离?探究.当x1≠x2,y1≠y2时,|P1P2|=?请简单说明理由.提示:可以,构造直角三角形利用勾股定理求解.答案:如图,在Rt △P1QP2中,|P1P2|2=|P1Q|2+|QP2|2,所以|P1P2|=?x2-x1?2+?y2-y1?2.即两点P1(x1,y1),P2(x2,y2)间的距离|P1P2|=?x2-x1?2+?y2-y1?2.你还能用其它方法证明这个公式吗?2.两点间距离公式的理解(1)此公式与两点的先后顺序无关,也就是说公式也可写成|P1P2|=?x2-x1?2+?y2-y1?2.(2)当直线P1P2平行于x轴时,|P1P2|=|x2-x1|.当直线P1P2平行于y轴时,|P1P2|=|y2-y1|.

倾斜角与斜率教学设计人教A版高中数学选择性必修第一册
(2)l的倾斜角为90°,即l平行于y轴,所以m+1=2m,得m=1.延伸探究1 本例条件不变,试求直线l的倾斜角为锐角时实数m的取值范围.解:由题意知(m"-" 1"-" 1)/(m+1"-" 2m)>0,解得1<m<2.延伸探究2 若将本例中的“N(2m,1)”改为“N(3m,2m)”,其他条件不变,结果如何?解:(1)由题意知(m"-" 1"-" 2m)/(m+1"-" 3m)=1,解得m=2.(2)由题意知m+1=3m,解得m=1/2.直线斜率的计算方法(1)判断两点的横坐标是否相等,若相等,则直线的斜率不存在.(2)若两点的横坐标不相等,则可以用斜率公式k=(y_2 "-" y_1)/(x_2 "-" x_1 )(其中x1≠x2)进行计算.金题典例 光线从点A(2,1)射到y轴上的点Q,经y轴反射后过点B(4,3),试求点Q的坐标及入射光线的斜率.解:(方法1)设Q(0,y),则由题意得kQA=-kQB.∵kQA=(1"-" y)/2,kQB=(3"-" y)/4,∴(1"-" y)/2=-(3"-" y)/4.解得y=5/3,即点Q的坐标为 0,5/3 ,∴k入=kQA=(1"-" y)/2=-1/3.(方法2)设Q(0,y),如图,点B(4,3)关于y轴的对称点为B'(-4,3), kAB'=(1"-" 3)/(2+4)=-1/3,由题意得,A、Q、B'三点共线.从而入射光线的斜率为kAQ=kAB'=-1/3.所以,有(1"-" y)/2=(1"-" 3)/(2+4),解得y=5/3,点Q的坐标为(0,5/3).

两条平行线间的距离教学设计人教A版高中数学选择性必修第一册
一、情境导学前面我们已经得到了两点间的距离公式,点到直线的距离公式,关于平面上的距离问题,两条直线间的距离也是值得研究的。思考1:立定跳远测量的什么距离?A.两平行线的距离 B.点到直线的距离 C. 点到点的距离二、探究新知思考2:已知两条平行直线l_1,l_2的方程,如何求l_1 〖与l〗_2间的距离?根据两条平行直线间距离的含义,在直线l_1上取任一点P(x_0,y_0 ),,点P(x_0,y_0 )到直线l_2的距离就是直线l_1与直线l_2间的距离,这样求两条平行线间的距离就转化为求点到直线的距离。两条平行直线间的距离1. 定义:夹在两平行线间的__________的长.公垂线段2. 图示: 3. 求法:转化为点到直线的距离.1.原点到直线x+2y-5=0的距离是( )A.2 B.3 C.2 D.5D [d=|-5|12+22=5.选D.]

两直线的交点坐标教学设计人教A版高中数学选择性必修第一册
1.直线2x+y+8=0和直线x+y-1=0的交点坐标是( )A.(-9,-10) B.(-9,10) C.(9,10) D.(9,-10)解析:解方程组{■(2x+y+8=0"," @x+y"-" 1=0"," )┤得{■(x="-" 9"," @y=10"," )┤即交点坐标是(-9,10).答案:B 2.直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,则k的值为( )A.-24 B.24 C.6 D.± 6解析:∵直线2x+3y-k=0和直线x-ky+12=0的交点在x轴上,可设交点坐标为(a,0),∴{■(2a"-" k=0"," @a+12=0"," )┤解得{■(a="-" 12"," @k="-" 24"," )┤故选A.答案:A 3.已知直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,若l1⊥l2,则点P的坐标为 . 解析:∵直线l1:ax+y-6=0与l2:x+(a-2)y+a-1=0相交于点P,且l1⊥l2,∴a×1+1×(a-2)=0,解得a=1,联立方程{■(x+y"-" 6=0"," @x"-" y=0"," )┤易得x=3,y=3,∴点P的坐标为(3,3).答案:(3,3) 4.求证:不论m为何值,直线(m-1)x+(2m-1)y=m-5都通过一定点. 证明:将原方程按m的降幂排列,整理得(x+2y-1)m-(x+y-5)=0,此式对于m的任意实数值都成立,根据恒等式的要求,m的一次项系数与常数项均等于零,故有{■(x+2y"-" 1=0"," @x+y"-" 5=0"," )┤解得{■(x=9"," @y="-" 4"." )┤

