-
人教A版高中数学必修二向量的减法运算教学设计
新知探究:向量的减法运算定义问题四:你能根据实数的减法运算定义向量的减法运算吗?由两个向量和的定义已知 即任意向量与其相反向量的和是零向量。求两个向量差的运算叫做向量的减法。我们看到,向量的减法可以转化为向量的加法来进行:减去一个向量相当于加上这个向量的相反向量。即新知探究(二):向量减法的作图方法知识探究(三):向量减法的几何意义问题六:根据问题五,思考一下向量减法的几何意义是什么?问题七:非零共线向量怎样做减法运算? 问题八:非零共线向量怎样做减法运算?1.共线同向2.共线反向小试牛刀判一判(正确的打“√”,错误的打“×”)(1)两个向量的差仍是一个向量。 (√ )(2)向量的减法实质上是向量的加法的逆运算. ( √ )(3)向量a与向量b的差与向量b与向量a的差互为相反向量。 ( √ )(4)相反向量是共线向量。 ( √ )

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
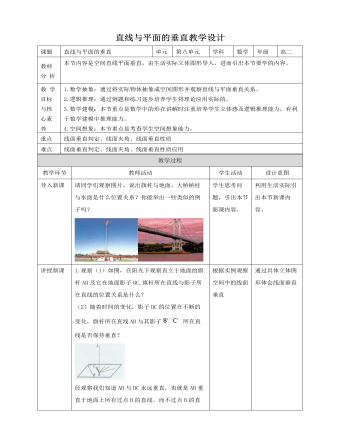
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

人教A版高中数学必修一全称量词与存在量词教学设计(2)
(4)“不论m取何实数,方程x2+2x-m=0都有实数根”是全称量词命题,其否定为“存在实数m0,使得方程x2+2x-m0=0没有实数根”,它是真命题.解题技巧:(含有一个量词的命题的否定方法)(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称量词命题还是存在量词命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.跟踪训练三3.写出下列命题的否定,并判断其真假:(1)p:?x∈R,x2-x+ ≥0;(2)q:所有的正方形都是矩形;(3)r:?x∈R,x2+3x+7≤0;(4)s:至少有一个实数x,使x3+1=0.【答案】见解析【解析】(1) p:?x∈R,x2-x+1/4<0.∵?x∈R,x2-x+1/4=(x"-" 1/2)^2≥0恒成立,∴ p是假命题.
人教A版高中数学必修二空间点、直线、平面之间的位置关系教学设计
9.例二:如图,AB∩α=B,A?α, ?a.直线AB与a具有怎样的位置关系?为什么?解:直线AB与a是异面直线。理由如下:若直线AB与a不是异面直线,则它们相交或平行,设它们确定的平面为β,则B∈β, 由于经过点B与直线a有且仅有一个平面α,因此平面平面α与β重合,从而 , 进而A∈α,这与A?α矛盾。所以直线AB与a是异面直线。补充说明:例二告诉我们一种判断异面直线的方法:与一个平面相交的直线和这个平面内不经过交点的直线是异面直线。10. 例3 已知a,b,c是三条直线,如果a与b是异面直线,b与c是异面直线,那么a与c有怎样的位置关系?并画图说明.解: 直线a与直线c的位置关系可以是平行、相交、异面.如图(1)(2)(3).总结:判定两条直线是异面直线的方法(1)定义法:由定义判断两条直线不可能在同一平面内.
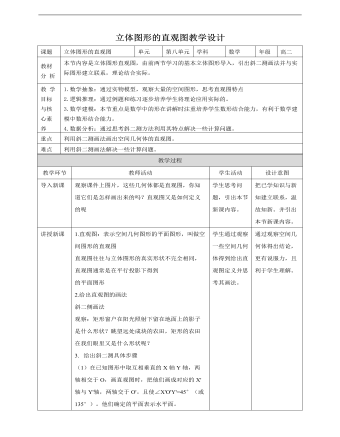
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
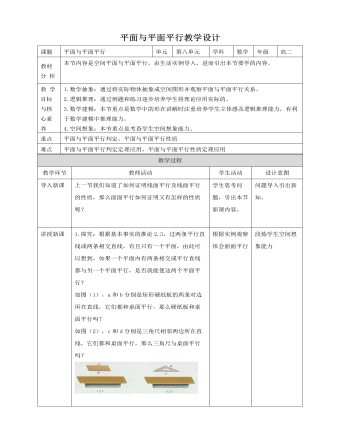
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教版新课标高中地理必修2第一章第一节人口的数量变化教案
材料四:印度提倡“只生一个好”——鼓励三人小家庭 生男生女都一样材料五:印度尼西亚《人口发展与幸福家庭法》材料六:我国基本国策 计划生育(小结)通过对以上材料的分析我们可以得出这样的结论,不同的国家应该采取不同的人口政策,对与发达国家来说人口增长缓慢,应采取鼓励生育,吸引移民的措施;发展中国家人口增长较快,实行控制人口的政策已经迫在眉睫。不论是发达国家还是发展中国家共同的目标就是实现环境人口和社会经济的协调发展。【课堂小结】这节课我们主要学习了人口的自然增长,影响人口自然增长的因素有哪些?(人口的自然增长率和人口的基数)世界人口的数量在不同的历史时期表现出不同的特征,同一历史时期的不同地区,人口数量的增长又有不同的特点。面对不同的人口形势,各国应采取不同的人口政策。

幼儿园大班健康教案:小甜心和小苦恼
二、活动准备 1、多媒体《小甜心和小苦恼》 2、微笑卡,音乐磁带,录音机 3、准备各种味道的东西及相应的表情图片,布置味道王国场景。三、活动过程 1、游戏导入:带领幼儿去心情味道王国感受不同味道的心情。 师:小朋友,今天老师带你们去一个好玩儿的地方——心情味道王国,在那个王国里所有人的心情都是和味道相联系的,我们一起去看一看吧。 带领幼儿做《表情歌》的律动去心情味道王国。2、品尝味道,感受心情。 师:心情味道王国到了,请小朋友自由地品尝味道,感受心情吧。 幼儿分散自由品尝体验,教师提醒幼儿注意卫生,保护口腔。 提问:你刚才品尝的是什么味道?心情怎样?

幼儿园小班体育教案:小熊盖房子(跑和跳)
2、学会按要求向指定方向跑和跳,并能有序地摆放小椅子。 3、在音乐游戏中,注意倾听音乐,并遵守游戏规则。 活动准备: 1、音乐磁带、 2、相距 40厘米 的平行线2条,两个大圆圈。 3、幼儿人手一张小椅子。 活动过程: 一、音乐游戏:数高楼 教师带领幼儿站成大圆圈,请4—6位幼儿扮演弟弟、妹妹站在圈外,引导幼儿随着音乐开展游戏活动。
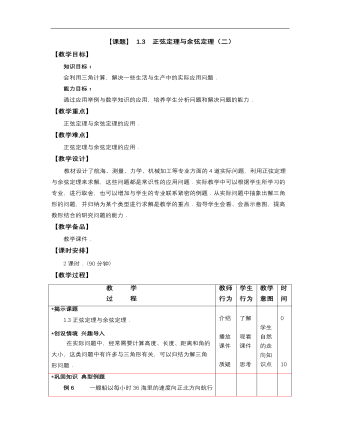
【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 在实际问题中,经常需要计算高度、长度、距离和角的大小,这类问题中有许多与三角形有关,可以归结为解三角形问题. 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点*巩固知识 典型例题 例6 一艘船以每小时36海里的速度向正北方向航行(如图1-9).在A处观察到灯塔C在船的北偏东方向,小时后船行驶到B处,此时灯塔C在船的北偏东方向,求B处和灯塔C的距离(精确到0.1海里). 图1-9 A 解因为∠NBC=,A=,所以.由题意知 (海里). 由正弦定理得 (海里). 答:B处离灯塔约为海里. 例7 修筑道路需挖掘隧道,在山的两侧是隧道口A和(图1-10),在平地上选择适合测量的点C,如果,m,m,试计算隧道AB的长度(精确到m). 图1-10 解 在ABC中,由余弦定理知 =. 所以 m. 答:隧道AB的长度约为409m. 例8 三个力作用于一点O(如图1-11)并且处于平衡状态,已知的大小分别为100N,120N,的夹角是60°,求F的大小(精确到1N)和方向. 图1-11 解 由向量加法的平行四边形法则知,向量表示F1,F2的合力F合,由力的平衡原理知,F应在的反向延长线上,且大小与F合相等. 在△OAC中,∠OAC=180°60°=120°,OA=100, AC=OB=120,由余弦定理得 OC= = ≈191(N). 在△AOC中,由正弦定理,得 sin∠AOC=≈0.5441, 所以∠AOC≈33°,F与F1间的夹角是180°–33°=147°. 答:F约为191N,F与F合的方向相反,且与F1的夹角约为147°. 引领 讲解 说明 引领 观察 思考 主动 求解 观察 通过 例题 进一 步领 会 注意 观察 学生 是否 理解 知识 点

【高教版】中职数学拓展模块:1.3《正弦定理与余弦定理》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.3正弦定理与余弦定理. *创设情境 兴趣导入 我们知道,在直角三角形(如图)中,,,即 ,, 由于,所以,于是 . 图1-6 所以 . 介绍 播放 课件 质疑 了解 观看 课件 思考 学生自然的走向知识点 0 10*动脑思考 探索新知 在任意三角形中,是否也存在类似的数量关系呢? c 图1-7 当三角形为钝角三角形时,不妨设角为钝角,如图所示,以为原点,以射线的方向为轴正方向,建立直角坐标系,则 两边取与单位向量的数量积,得 由于设与角A,B,C相对应的边长分别为a,b,c,故 即 所以 同理可得 即 当三角形为锐角三角形时,同样可以得到这个结论.于是得到正弦定理: 在三角形中,各边与它所对的角的正弦之比相等. 即 (1.7) 利用正弦定理可以求解下列问题: (1)已知三角形的两个角和任意一边,求其他两边和一角. (2)已知三角形的两边和其中一边所对角,求其他两角和一边. 详细分析讲解 总结 归纳 详细分析讲解 思考 理解 记忆 理解 记忆 带领 学生 总结 20

镇2022年上半年工作总结和下半年工作打算
一、2022年上半年工作开展情况(一)强化项目投资,落实产业发展“有信心” 坚持规划引领,以项目为抓手,结合大熊猫国家公园南入口社区建设,打造**国际森林康养度假产业园。一是加快项目落地,积极对接荥发展集团、徐氏文旅集团、中铁五局,统筹推进熊猫翠竹长廊、经河防洪治理工程、万年村方竹基地、沉浸式体验中心、熊猫会客厅、熊猫之眼露营地建设。二是完善项目库储备,已包装策划基础设施、环境保护、重大产业、社会发展等方面入库储备33个,动态投资约160亿元,正在开展前期可研、初设的有12个约18亿。三是强势推进招商固投,截至目前,已外出进行招商引资15次,完成争取上级资金28万元。**鲑鳟鱼养殖基地建设项目、**度假民宿酒店建设项目已达成初步投资意向。加快固投申报速度,已完成固投2700万元,完成全年任务53%。

镇2024年上半年工作总结和下半年工作安排
二是要在推进乡村振兴上求突破。深入实施乡村振兴战略,推动农业升级、农村进步、农民发展。高标准开展农村人居环境提升工作,提升303国道沿线和偏远村屯人居环境,全面抓好垃圾治理、污水处理、厕所改造“三大革命”,努力实现村村干净、户户整洁。严格执行河长制、林长制、田长制,重点整治乱采、乱伐、乱占、乱建等问题,切实维护好“水清、山绿、景美”的良好生态环境。三是要在民生改善上求突破。全力发展产业,努力扩大就业,积极支持创业,不断增加群众的经营性收入和财产性收入。扎实做好贫困人员监测工作,确保监测贫困人员不返贫。不断完善社会保障体系,做好各类救助资金发放和弱势群体、特困家庭救助。大力发展社会事业,进一步改善办学条件和基层公共卫生服务水平,积极开展形式多样的文体活动,逐步提升基本公共服务水平。

市卫健委2024年上半年工作总结和下半年工作安排
以农村为重点深化爱国卫生运动,新增省卫生村xxx个以上,新增省健康村xxx个以上,力争国家卫生城市复评通过率、国家卫生县城复评通过率、国家卫生乡镇创建复评通过率达xxx%,居民健康素养水平达xx%以上。(二)超常规推进医学高峰建设。加快推进国家“双中心”创建,推动温医大附属眼视光医院争创国家医学中心,争取市中西医结合医院滨江院区列入建设类国家区域医疗中心项目,落地国家传染病医学中心xx中心;重点培育x家高水平研究型医院,力争新增三甲医院x家;实施临床重点专科建设三年行动计划,推动做精尖峰学科、做强优势学科、发展潜力学科,争取一批学科纳入新一轮省级重点学科发展计划。推动在温省级医院和市属医院加强内涵建设,减少常见病多发病门诊服务,提升CMI和疑难病例占比等关键指标,争取在公立医院国考中进等升位。编制区域医疗资源布局专项规划,优化专科医院发展布局。

市国资委2024年上半年工作总结和下半年工作思路
(四)抓监管防风险,进一步凝聚企业活力。一是强化综合监督。修订《XX市企业国有资产损失责任追究试行办法》,规范追责标准和工作流程,确保责任追究工作有章可循、规范有序。加强内部审计和违规问题线索调查,合理运用提示函等工作规则,倒逼企业规范经营、提质增效。二是坚持激励激活。开展“大调研大走访大服务大解题”活动,立足“管资本”为主梳理一批对市属国企的授权、放权管理事项,建立完善授权制度与授权清单。深入推进市属国企综合考核,以效益为主导向调整工资总额决定机制,试点推行企业年金和中长期激励方式。三是防范财务风险。优化完善全市国企融资情况和债券发行情况月度统计分析和风险预警防控制度,及时梳理处置潜在的风险隐患。推广企业“资金池”管理模式,加强企业内部资金管理,全面提高资金使用效率。持续迭代升级“国资大脑”,进一步完善委企之间信息共享和业务协同机制,发挥实时智能监控预警作用。

2024年上半年街道工作总结和下半年工作重点
二、下半年工作思路围绕“打造浙中增长极建设未来新中心”战略目标,聚焦平安护航亚运主题主线,下半年重点打好五大攻坚战。(一)坚决打好产业升级攻坚战。围绕数字经济“一号发展工程”,重点推进新材料、汽车等细分行业数字化改造,力争实现省级“未来工厂”零的突破。深入开展“腾笼换鸟”攻坚行动,9月底前完成低效用地整治1000亩的年度目标,配合新区完成自贸区土地连片整治工作。加强乡镇科技创新,推进单项冠军、专精特新“小巨人”等优秀企业培养,保质保量完成新增省科技型中小企业28家、国家高新技术企业5家、规上企业研发机构24家的任务目标。全心全意优环境,利用XX商会等资源,建设企业困难帮扶平台,努力做到“妈妈式”服务和“保镖式”保护。

疾控中心2023年上半年工作总结和下半年工作计划
(六)进一步加强疫苗安全管理我县已经实现疫苗从县级储存库到各接种点全程冷链运输,已冷链远转8次,全程温度自动监控,杜绝自提疫苗现象,确保疫苗安全。下半年工作计划及工作要点1、加强培训工作,计划举办1次结核病防治管理培训班,提高各级医疗、防疫人员水平,促进结防项目工作质量的提高。2、协调县总医院规范做好痰涂片、痰培养和分子生物学诊断工作。督促县总医院认真做好可疑耐药病人的筛查和痰培养工作,对培养阳性的病人积极推送至市疾控,进行药敏实验。3、加强督导管理,实行县、乡分级管理,分级督导。切实做好患者的随访管理工作,县疾控中心计划定期对28个乡镇卫生院(社区卫生服务中心)开展常态化的现场工作指导。全年将按季度对全县结核病防治工作进行督导通报。

街道2024年上半年工作总结和下半年工作重点
(四)坚决打好除险保安攻坚战。健全完善网格化治理模式,注重发挥基层网格员、村“两委”干部、联村干部的作用,构建覆盖全域、反应迅速、处置有效的基层网格治理格局。强化社会综合治理,持续迭代升级“141”基层社会治理模式,深化“大综合一体化”行政执法改革,滚动开展安全生产和消防安全系列专项活动,将重点人员牢牢稳控在基层,确保亚运会平稳举办。持续深化“法亮调解室”“一村一警”等社会治理品牌,及时总结提炼全处面上基层治理的经验做法,最终以治理品牌进一步提升治理效果。(五)坚决打好民生改善攻坚战。深入推进扩中提底,加快村级“一事一议”项目建设和农民自建房审批,深化推进“共富工坊”,确保今年22个行政村全部完成经营性收入**万以上。





