-

关于清明节的演讲稿:校领导清明节国旗下讲话稿
关于清明节的演讲稿:校领导清明节国旗下讲话稿各位老师、各位同学:!本周我们即将迎来我国传统节日——清明节,今年的清明节也是新假期制度实行后的个传统节日。清明既是节日也是节气之一,这是一个与二十四节气重合的节日。每年4月5日前后,我国黄河中下游及其以南地区平均气温一般在10℃以上。这时我们大部分地区气候温暖、草木萌茂,改变冬季寒冷枯黄的景象。清明一到,气温升高,雨量增多,正是春耕春种的大好时节,故有“清明前后,点瓜种豆”、“植树造林,莫过清明”的农谚,可见这个节气与农业有着密切的关系。而清明节祭扫的起源,于中国传统的土葬,由于土葬后的水土流失,因此每年定在清明节时祭扫祖先的墓地。同时结合清明节时的气候特点又可以进行踏青活动,放风筝等等,可以说是一个既肃穆又轻松的节日。而随着现代社会的发展,清明节这类产生于农耕文化下的传统节日逐渐失去了产生时的文化背景,在现在的年轻人眼中可能只是一种形式而已。

关于清明节的演讲稿:清明节国旗下讲话稿
关于清明节的演讲稿:清明节国旗下讲话稿亲爱的老师、同学们:早上好!我们走进阳光的四月,一切都是新绿的。然而当五星红旗冉冉升起的时候,你的脑海中是否会浮现出这样一篇诗的景象呢?南北山头多墓田,清明祭扫各纷然。纸灰飞作白蝴蝶,泪血染成红杜鹃。你是否会想起那段战火纷飞,硝烟弥漫的日子了吗?每当这个时*候,我们的眼前就会浮现出董存瑞舍身炸碉堡的身影,耳边就会响起夏明翰“砍头不要紧,只要主义真”的誓言;每当这个时候,我们就会想起长征路上倒下的年轻战士,渣滓洞里昂首挺立的员刘胡兰,每当这个时候,我们就会想起那些建设祖国鞠躬尽瘁的模范人物……我想你们应该记得,在中华民族面临生死存亡的危险时刻,是先烈们用自己的血肉之躯筑起了钢铁长城,与日本帝国主义侵略者进行着殊死拼搏。他们倒下了,但成千上万“不愿做奴隶的人们”站起来了,他们高唱着“义勇军进行曲”,去继承你们未完的事业;是先烈们把对国家、对劳苦大众的爱化作战斗中同敌人拼杀的精神力量,不怕牺牲,勇往直前,*以摧枯拉朽之势,宣布了蒋家王朝的灭亡,建立了人民当家作主的新中国

关于防灾国旗下演讲稿讲话稿三篇
篇一各位老师,同学们:1.如果正在上课,地震来了,同学们一定在要在老师的指挥下,迅速抱头,闭眼,赶快躲在自己的课桌下面。2.次震感过后,大概也就是在几十秒钟,还是在老师的指挥下迅速、有序的,抱头,撤离教室,在楼道里不要惊慌,又要喊叫,不要拥挤,避免踩伤,摔伤,冲出教学楼,冲向操场。3.如果正在操场上上体育课,可原地不动,蹲下或趴下,双手护着头部,注意避开高大建筑物。4.应该强调的是千万不要跳楼!不要在窗台边上去!也不要到走廊的护栏边上去,更不要尖叫,不要拥挤,迅速撤离教室、教学楼。刚才学老师在说到地震来了怎么办的时候,同学们注意到了没有,有两个关键词:一个是“在老师的指挥下”;一个是波地震来时“桌子”非常重要。下面老师就来说一说发生在四川大地震时发生的两个实例。首先请同学们、老师们记住一个伟大而平凡的名字―――谭千秋。他是四川省德阳市汉旺镇东汽中学的老师。地震发生时他正在上课,强烈的地震突然发生时,谭老师立即组织学生钻桌子下面。而霎间倒塌的水泥板向学生砸来时,谭老师立刻张开双臂扑向桌子上面,用血肉的身躯护佑着桌子下面的四位学生,两天后四位学生全部生还,而他的老师―――谭千秋,成了他们和我们永远怀念和敬仰的伟大而光荣的人民教师。“人们发现他的时候,他双臂张开着趴在课桌上,身下还死死地护着4个学生,4个学生都活了!”一位救援的解放军战士向记者描述着当时的情景。

XX年中秋节国旗下演讲稿讲话稿三篇
篇一尊敬老师,亲爱的同学们:大家好!中秋的脚步越来越近了,满月的光芒,在一个又一个的夜晚,悄悄临近。“不知天上宫阙,今夕是何年。”天上的日子似乎比人间要慢许多,但是,同学们,不要感叹时光的流逝,也不要将时光虚度。每一天本都它的有价值所在,将时光握紧,用分分秒秒来创造充实的时光。将目光着手书本,而不是漫画。因为我们已经长大。将身心专注学习,而不是玩耍。因为我们不再幼小。时光的虚度,只会使人感到老去得更快;充实的学习,则会让人领略到成功于欣喜,光阴也不禁放慢了脚步。多少轮中秋明月在夜里悄悄流逝,又有多少圆月,将在不久来临?我们步入初中,我们渐渐成熟,我们有了自己的理想,如明月般美好的。但是,我们可以尽情地梦想,又如何去打捞那轮美丽的明月。“人间悲欢离合,月有阴晴圆缺。”挫折在所难免,面对着失败,我们不可以被打败。

合 同 书
甲乙双方本着友好协商,互惠互利的原则,依据《中华人民共和国合同法》及中华人民共和国其他相关法律规定,就乙方承接甲方 淘宝店铺设计 项目相关事宜达成如下协议:1.项目总则 1.1 服务内容: 1.2 施工日期: 1.3 施工地点: 2.合同价款: 总价:即人民币: 3.付款方式合同签定两日内通过支付宝支付总价款,即人民币 元于淘宝第三方;乙方根据淘宝店铺美工包月套餐详情页的要求配合甲方的运营需要完成设计任务,服务时间为一个月。4.甲方责任与权利1)甲方应提供乙方所需资料,并与甲方共同确认设计风格。2)甲方不可再设计过程中随意更改设计风格。3)甲方应积极配合乙方的设计需求。4)因甲方反复提出修改意见导致乙方工作不能按时完成,乙方可延期交货,时间由双方协议商定。5)甲方有权对乙方的设计提出建议和思路,以使乙方设计的作品更符合甲方企业文化内涵。6)甲方有权对乙方所设计的作品提出修改意见。7)甲方在付清所有设计费用后享有设计作品的所有权、使用权和修改权。

月 嫂 合 同
xxxx月嫂家政服务有限公司月嫂服务合同双方承诺:本合同以平等,自愿,公平,公正的原则为基础,在不违反中华人民共和国法律所规定的范围内签订。聘请月嫂须知 :客户聘用月嫂,应到经政府主管部门登记注册、以月嫂家政服务为经营范围、具有法人资格的正规月嫂家政服务机构,不要在非法劳务市场中招雇。请您结合自己的情况选择月嫂服务项目,并按此规定办理:1、个人用户持居民身份证、户口本、居住证明或护照;单位用户持有合法证件及公函.2、有稳定的经济收入来源并有能力支付相关费用。3、要正确看待月嫂家政服务行业,允许月嫂服务员有一周的适应过程,尊重月嫂服务员的人格,禁止打骂、歧视或侮辱月嫂服务员,不得要求月嫂服务员工作范围以外的工作内容。 4、愿意遵守国家和地区月嫂家政服务业的行业规则,配合月嫂家政服务机构的工作。5、能如实填写客户信息登记表。 6、签订合同时知晓并认可双方的协商价格,选定服务项目、签订合同并交纳相关费用后,公司将为您提供相应期限的选项服务。 7、月嫂服务员在您家工作时,若出现身体不适或其他疾病,发生意外事件,请您务必发扬人道主义精神,及时灵活做出处理,并通报月嫂家政服务机构。由于雇主(甲方)有雇用母婴护理员(简称月嫂)方面的需求,xxxx月嫂家政服务有限公司(乙方)愿意为甲方提供“母婴护理”服务。根据《中华人民共和国合同法》、《中华人民共和国侵权责任法》和《中华人民共和国消费者权益保护法》及其他有关法律、法规的规定,甲乙双方遵循平等、自愿、诚实信用原则,并承诺为甲方提供专业、优质、安全的“母婴护理”服务,就月嫂服务相关事宜签订本合同。

广 告 合 同
根据《中华人民共和国广告法》、《中华人民共和国合同法》的规定,甲乙双方在平等、自愿的基础上,本着友好协商、互惠互利的原则,就甲方委托乙方制作、发布广告等相关事宜,达成如下协议:第一条 合同概况(一) 广告项目名称: (二) 广告发布地点: (三) 广告发布形式: (四) 广告规格数量: (五) 广告质量标准: (六) 广告发布期限:1.共 天,自 年 月 日至 年 月 日。2.实际发布起始日期推迟的,截止日期相应顺延。3.合同期满后,在同等条件下,甲方有优先续约权。 第二条 合同总价款及支付方式(一) 合同总价款为:(大写)人民币 (小写) 元整,此价款包含制作费、设置费、报批费、占地费、电费、保险费、维修费、撤除费用、税金,以及同本广告发布相关的其他所有费用。(合同价款是固定的,乙方无权以任何理由要求增加合同价格,如市场物价上涨,货币价格浮动,生活费用提高,工资的基限提高,调整税法及税务。此价款包含税款。) (二) 付款方式:本合同生效后,甲方预付合同总价款的20%款项给乙方。验收合格后,付至合同总价款的95%,剩余5%为质保金。质保期自广告经验收合格后至广告发布期限届满之日,待质保期满后甲方将质保金一次付清。
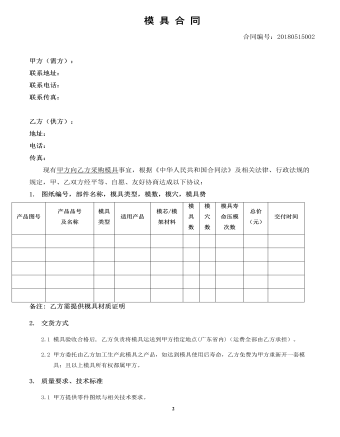
模 具 合 同
现有甲方向乙方采购模具事宜,根据《中华人民共和国合同法》及相关法律、行政法规的规定,甲、乙双方经平等、自愿、友好协商达成以下协议:1. 图纸编号,部件名称,模具类型,模数,模穴,模具费 产品图号 产品品号及名称 模具类型 适用产品 模芯/模架材料 模具数 模穴数 模具寿命压模次数 总价(元) 交付时间备注: 乙方需提供模具材质证明2. 交货方式2.1 模具验收合格后, 乙方负责将模具运送到甲方指定地点(广东省内)(运费全部由乙方承担)。2.2 甲方委托由乙方加工生产此模具之产品,如达到模具使用后寿命,乙方免费为甲方重新开一套模具;且以上模具所有权都属甲方。3. 质量要求、技术标准3.1 甲方提供零件图纸与相关技术要求。3.2 乙方根据甲方零件图纸和相关技术要求进行模具设计,并制作完成相关模具设计图纸。乙方须将该图纸提交甲方技术人员确认后再进行具体的模具制作(即乙方须提供模具结构图并得到甲方确认,方可制作模具)。3.3 乙方必须按甲方要求填写《模具清单》确保模具所生产的产品零件无缺陷,《模具清单》随模具合同同时发放,填写并需乙方签字盖章生效。3.4 乙方必须确保模具所使用的材质与报价时所填《模具清单》的材质一致,如有发现材质问题,甲方有权要求乙方按本合同模具总价的2倍进行赔偿。4. 产品保密要求4.1 甲方提供的图纸、模具的所有权、知识产权归属甲方,乙方不得向第三人披露。未经甲方允许,乙方不得根据图纸、模具进行加工销售。否则,甲方有权终止合同,停止支付所有货款,有权要求乙方按模具总价的2倍予以赔偿,并保留追究乙方法律责任的权利。

借 款 合 同
甲、乙双方依据《中华人民共和国合同法》等有关法律、法规和规章的相关规定,就甲方向乙方借款事宜,经充分协商一致,特订立本合同,并共同遵守。第一条 借款金额、期限1.1 本合同项下借款金额为人民币(大写) ;(小写) 。1.2 本合同项下借款期限为(大写) (个月、年),自 年 月 日至 年 月 日。实际借款期限以借款借据或乙方出借款项实际到达甲方账户为准。借款借据为本合同的有效组成部分,与本合同具有同等法律效力。第二条 借款用途2.1 本合同项下出借款项用于 未经乙方书面同意,甲方不得改变借款用途。2.2 甲方承诺如擅自改变借款用途,或将借款用于非法活动,造成的任何后果及法律责任概由甲方自行承担,与乙方无关。第三条 贷款利率、计息、结息3.1 本合同项下的借款利率为月利率,利率为 %,在约定的借款期间内,该利率保持不变,但甲、乙双方另有约定的,从其约定。3.2 计息:贷款利息从出借款项实际到达甲方账户之日起开始计算。本合同项下的贷款按日计息,日利率=月利率/30。

人教A版高中数学必修一三角函数的应用教学设计(2)
本节课是在学习了三角函数图象和性质的前提下来学习三角函数模型的简单应用,进一步突出函数来源于生活应用于生活的思想,让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力.课程目标1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.2.实际问题抽象为三角函数模型. 数学学科素养1.逻辑抽象:实际问题抽象为三角函数模型问题;2.数据分析:分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立数学模型; 3.数学运算:实际问题求解; 4.数学建模:体验一些具有周期性变化规律的实际问题的数学建模思想,提高学生的建模、分析问题、数形结合、抽象概括等能力.

人教A版高中数学必修一函数模型的应用教学设计(2)
本节通过一些函数模型的实例,让学生感受建立函数模型的过程和方法,体会函数在数学和其他学科中的广泛应用,进一步认识到函数是描述客观世界变化规律的基本数学模型,能初步运用函数思想解决一些生活中的简单问题。课程目标1.能利用已知函数模型求解实际问题.2.能自建确定性函数模型解决实际问题.数学学科素养1.数学抽象:建立函数模型,把实际应用问题转化为数学问题;2.逻辑推理:通过数据分析,确定合适的函数模型;3.数学运算:解答数学问题,求得结果;4.数据分析:把数学结果转译成具体问题的结论,做出解答;5.数学建模:借助函数模型,利用函数的思想解决现实生活中的实际问题.重点:利用函数模型解决实际问题;难点:数模型的构造与对数据的处理.

人教A版高中数学必修一充分条件与必要条件教学设计(2)
【例3】本例中“p是q的充分不必要条件”改为“p是q的必要不充分条件”,其他条件不变,试求m的取值范围.【答案】见解析【解析】由x2-8x-20≤0得-2≤x≤10,由x2-2x+1-m2≤0(m>0)得1-m≤x≤1+m(m>0)因为p是q的必要不充分条件,所以q?p,且p?/q.则{x|1-m≤x≤1+m,m>0}?{x|-2≤x≤10}所以m>01-m≥-21+m≤10,解得0<m≤3.即m的取值范围是(0,3].解题技巧:(利用充分、必要、充分必要条件的关系求参数范围)(1)化简p、q两命题,(2)根据p与q的关系(充分、必要、充要条件)转化为集合间的关系,(3)利用集合间的关系建立不等关系,(4)求解参数范围.跟踪训练三3.已知P={x|a-4<x<a+4},Q={x|1<x<3},“x∈P”是“x∈Q”的必要条件,求实数a的取值范围.【答案】见解析【解析】因为“x∈P”是x∈Q的必要条件,所以Q?P.所以a-4≤1a+4≥3解得-1≤a≤5即a的取值范围是[-1,5].五、课堂小结让学生总结本节课所学主要知识及解题技巧

人教A版高中数学必修一充分条件与必要条件教学设计(1)
本课是高中数学第一章第4节,充要条件是中学数学中最重要的数学概念之一, 它主要讨论了命题的条件与结论之间的逻辑关系,目的是为今后的数学学习特别是数学推理的学习打下基础。从学生学习的角度看,与旧教材相比,教学时间的前置,造成学生在学习充要条件这一概念时的知识储备不够丰富,逻辑思维能力的训练不够充分,这也为教师的教学带来一定的困难.“充要条件”这一节介绍了充分条件,必要条件和充要条件三个概念,由于这些概念比较抽象,中学生不易理解,用它们去解决具体问题则更为困难,因此”充要条件”的教学成为中学数学的难点之一,而必要条件的定义又是本节内容的难点.A.正确理解充分不必要条件、必要不充分条件、充要条件的概念;B.会判断命题的充分条件、必要条件、充要条件.C.通过学习,使学生明白对条件的判定应该归结为判断命题的真假.D.在观察和思考中,在解题和证明题中,培养学生思维能力的严密性品质.

人教A版高中数学必修一不同函数增长的差异教学设计(2)
本节课在已学幂函数、指数函数、对数函数的增长方式存在很大差异.事实上,这种差异正是不同类型现实问题具有不同增长规律的反应.而本节课重在研究不同函数增长的差异.课程目标1.掌握常见增长函数的定义、图象、性质,并体会其增长的快慢.2.理解直线上升、对数增长、指数爆炸的含义以及三种函数模型的性质的比较,培养数学建模和数学运算等核心素养.数学学科素养1.数学抽象:常见增长函数的定义、图象、性质;2.逻辑推理:三种函数的增长速度比较;3.数学运算:由函数图像求函数解析式;4.数据分析:由图象判断指数函数、对数函数和幂函数;5.数学建模:通过由抽象到具体,由具体到一般的数形结合思想总结函数性质.重点:比较函数值得大小;难点:几种增长函数模型的应用.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。

人教A版高中数学必修一不同增长函数的差异教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.3节《不同增长函数的差异》 是在学习了指数函数、对数函数和幂函数之后的对函数学习的一次梳理和总结。本节提出函数增长快慢的问题,通过函数图像及三个函数的性质,完成函数增长快慢的认识。既是对三种函数学习的总结,也为后续导数的学习做了铺垫。培养和发展学生数学直观、数学抽象、逻辑推理和数学建模的核心素养。1.了解指数函数、对数函数、幂函数 (一次函数) 的增长差异.2、经过探究对函数的图像观察,理解对数增长、直线上升、指数爆炸。培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;3、在认识函数增长差异的过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学应用的意识,探索数学。 a.数学抽象:函数增长快慢的认识;b.逻辑推理:由特殊到一般的推理;

人教A版高中数学必修一对数函数的概念教学设计(1)
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.4.1节《对数函数的概念》。对数函数是高中数学在指数函数之后的重要初等函数之一。对数函数与指数函数联系密切,无论是研究的思想方法方法还是图像及性质,都有其共通之处。相较于指数函数,对数函数的图象亦有其独特的美感。学习中让学生体会在类比推理,感受图像的变化,认识变化的规律,这是提高学生直观想象能力的一个重要的过程。为之后学习数学提供了更多角度的分析方法。培养学生逻辑推理、数学直观、数学抽象、和数学建模的核心素养。1、理解对数函数的定义,会求对数函数的定义域;2、了解对数函数与指数函数之间的联系,培养学生观察问题、分析问题和归纳问题的思维能力以及数学交流能力;渗透类比等基本数学思想方法。3、在学习对数函数过程中,使学生学会认识事物的特殊性与一般性之间的关系,培养数学应用的意识,感受数学、理解数学、探索数学,提高学习数学的兴趣。

人教A版高中数学必修一对数函数的概念教学设计(2)
对数函数与指数函数是相通的,本节在已经学习指数函数的基础上通过实例总结归纳对数函数的概念,通过函数的形式与特征解决一些与对数函数有关的问题.课程目标1、通过实际问题了解对数函数的实际背景;2、掌握对数函数的概念,并会判断一些函数是否是对数函数. 数学学科素养1.数学抽象:对数函数的概念;2.逻辑推理:用待定系数法求函数解析式及解析值;3.数学运算:利用对数函数的概念求参数;4.数学建模:通过由抽象到具体,由具体到一般的思想总结对数函数概念.重点:理解对数函数的概念和意义;难点:理解对数函数的概念.教学方法:以学生为主体,采用诱思探究式教学,精讲多练。教学工具:多媒体。一、 情景导入我们已经研究了死亡生物体内碳14的含量y随死亡时间x的变化而衰减的规律.反过来,已知死亡生物体内碳14的含量,如何得知死亡了多长时间呢?进一步地,死亡时间t是碳14的含量y的函数吗?

人教A版高中数学必修一函数y=Asin(ωχ+φ)教学设计(1)
本节课选自《普通高中课程标准实验教科书数学必修1》5.6.2节 函数y=Asin(ωx+φ)的图象通过图象变换,揭示参数φ、ω、A变化时对函数图象的形状和位置的影响。通过引导学生对函数y=sinx到y=Asin(ωx+φ)的图象变换规律的探索,让学生体会到由简单到复杂、由特殊到一般的化归思想;并通过对周期变换、相位变换先后顺序调整后,将影响图象变换这一难点的突破,让学生学会抓住问题的主要矛盾来解决问题的基本思想方法;通过对参数φ、ω、A的分类讨论,让学生深刻认识图象变换与函数解析式变换的内在联系。通过图象变换和“五点”作图法,正确找出函数y=sinx到y=Asin(ωx+φ)的图象变换规律,这也是本节课的重点所在。提高学生的推理能力。让学生感受数形结合及转化的思想方法。发展学生数学直观、数学抽象、逻辑推理、数学建模的核心素养。

人教A版高中数学必修一函数的表示法教学设计(1)
本节课选自《普通高中课程标准数学教科书-必修一》(人教A版)第三章《函数的概念与性质》,本节课是第2课时,本节课主要学习函数的三种表示方法及其简单应用,进一步加深对函数概念的理解。课本从引进函数概念开始就比较注重函数的不同表示方法:解析法,图象法,列表法.函数的不同表示方法能丰富对函数的认识,帮助理解抽象的函数概念.特别是在信息技术环境下,可以使函数在形与数两方面的结合得到更充分的表现,使学生通过函数的学习更好地体会数形结合这种重要的数学思想方法.因此,在研究函数时,要充分发挥图象的直观作用.课程目标 学科素养A.在实际情景中,会根据不同的需要选择恰当的方法(解析式法、图象法、列表法)表示函数;B.了解简单的分段函数,并能简单地应用;1.数学抽象:函数解析法及能由条件求函数的解析式;2.逻辑推理:求函数的解析式;

人教A版高中数学必修一函数的表示法教学设计(2)
课本从引进函数概念开始就比较注重函数的不同表示方法:解析法,图象法,列表法.函数的不同表示方法能丰富对函数的认识,帮助理解抽象的函数概念.特别是在信息技术环境下,可以使函数在形与数两方面的结合得到更充分的表现,使学生通过函数的学习更好地体会数形结合这种重要的数学思想方法.因此,在研究函数时,要充分发挥图象的直观作用.在研究图象时,又要注意代数刻画以求思考和表述的精确性.课本将映射作为函数的一种推广,这与传统的处理方式有了逻辑顺序上的变化.这样处理,主要是想较好地衔接初中的学习,让学生将更多的精力集中理解函数的概念,同时,也体现了从特殊到一般的思维过程.课程目标1、明确函数的三种表示方法;2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;3、通过具体实例,了解简单的分段函数,并能简单应用.

