-

大班数学:新车出厂课件教案
活动准备:数字2、6、8、8四套、记录纸4张车牌号码 活动流程:一、交流城市新车感受城市变化,给生活带来得方便1、师:张老师买了辆新车,你们看!(出示别克凯悦)你还知道别克凯悦啊,那你还知道哪些车?2、新车拿到了,我要上路了,现在能出发了吗?(没有挂牌照)没有牌照会怎么样?排列汽车牌照 教师小结:牌照就象一辆车子的身份、名字,每辆车的车牌都不一样。上海一个牌照很贵呢!

大班数学:小蜻蜓捉害虫课件教案
2、在操作活动中不断探索数的多种分法,并学会记录。3、发展动手操作能力及多维度思维能力。活动准备:教具:稻田背景图一张,木珠做成的虫子一条,刀笔一只,记录卡一张,练习卡片若干。 学具:木珠做成的虫子若干,记录卡人手一份,刀笔人手一份。

大班数学:做棒棒糖课件教案
活动准备:橡皮泥五块,玻璃纸五张(红、两色),木棒五根(四根粗,一根细),5以内加减卡片一套。活动过程:1、做棒糖:让孩子在规定的时间内将橡皮泥捏成球体状或正方体状,插上木棒后在包上玻璃纸(包出自己喜欢的式样)。2、数一数:自己做了几根棒糖?用了几块橡皮泥?几张玻璃纸?几根木棒?

大班数学活动:二等分课件教案
2、体会二等分给我们生活带来的便捷、美化作用。活动材料;教具:小蚂蚁两个、蛋糕一块、二等份图卡10张学具:长方形纸、剪刀、尺、毛线、包装纸;吸管、圆片、三角形、正方形;硬币、蚕豆、雪花片、纽扣、小碗;量杯6个、天平、蛋糕、番茄、豆腐干、刀子、菜板、橡皮泥等。活动过程:1、幼儿将长方形纸进行二等份。(1)班上请来了两位小客人,看看是谁?它们还带来了最喜欢吃的蛋糕,可是只有一块蛋糕,两人都想吃,怎么办?(2)请一位幼儿动手试一试,有什么办法知道这两块一样大呢?(重叠)(3)教师小结:把蛋糕分成一样大的两份,这种方法叫二等份。想想蛋糕除了这样分,还有不一样的分法吗?每位小朋友面前都有一张像蛋糕一样的长方形纸,请你想出和别人不同的方法进行二等份?

大班数学:小鸡搬家课件教案
2、对加减运算感兴趣,在游戏情境中体验快乐。 3、书写和表达、动手操作相结合,积极参加数学加减活动。 二、活动准备: 物质准备:气球上打印7的组成;背景小鸡的家、8的一二组加减(活动的、书写的、游戏的)、记号笔、抹布、花娃娃、夹子、数字1-8 经验准备:学过8的组成,对7以内加减有一定理解。 三、活动过程: (一)复习8的组成(情境——庆祝小鸡搬家) 游戏:放气球(歌曲问答:气球上面有题目,我们大家来放气球,8可以分成1和几,1和几组成8……)

北师大初中数学八年级上册应用二元一次方程组——里程碑上的数2教案
提示:要学会在图表中用含未知数的代数式表示出要分析的量;然后利用相等关系列方程。2.Flash动画,情景再现.3.学法小结:(1)对较复杂的问题可以通过列表格的方法理清题中的未知量、已知量以及等量关系,这样,条理比较清楚.(2)借助方程组解决实际问题.设计意图:生动的情景引入,意在激发学生的学习兴趣;利用图表帮助分析使条理清楚,降低思维难度,并使列方程解决问题的过程更加清晰;学法小结,着重强调分析方法,养成归纳小结的良好习惯。实际效果:动画引入,使数字问题变的更有趣,确实有效地激发了学生的兴趣,学生参与热情很高;借助图表分析,有效地克服了难点,学生基本都能借助图表分析,在老师的引导下列出方程组。4.变式训练师生共同研究下题:有一个三位数,现将最左边的数字移到最右边,则比原来的数小45;又知百位数字的9倍比由十位数字和个位数字组成的两位数小3,试求原来的3位数.

北师大初中数学八年级上册应用二元一次方程组——里程碑上的数1教案
A、B两码头相距140km,一艘轮船在其间航行,顺水航行用了7h,逆水航行用了10h,求这艘轮船在静水中的速度和水流速度.解析:设这艘轮船在静水中的速度为xkm/h,水流速度为ykm/h,列表如下,路程 速度 时间顺流 140km (x+y)km/h 7h逆流 140km (x-y)km/h 10h解:设这艘轮船在静水中的速度为xkm/h,水流速度为ykm/h.由题意,得7(x+y)=140,10(x-y)=140.解得x=17,y=3.答:这艘轮船在静水中的速度为17km/h,水流速度为3km/h.方法总结:本题关键是找到各速度之间的关系,顺速=静速+水速,逆速=静速-水速;再结合公式“路程=速度×时间”列方程组.三、板书设计“里程碑上的数”问题数字问题行程问题数学思想方法是数学学习的灵魂.教学中注意关注蕴含其中的数学思想方法(如化归方法),介绍化归思想及其运用,既可提高学生的学习兴趣,开阔视野,同时也提高学生对数学思想的认识,提升解题能力.
人教版高中语文必修3《杜甫诗三首 咏怀古迹》教案
“千载琵琶作胡语,分明怨恨曲中论。”“怨恨”两字点明全篇主旨。千百年来,琵琶所演奏的总是从匈奴传来的撩人愁思的胡乐,正是昭君在诉说着她的怨恨!这两句从侧面烘托昭君的形象,既有对她的赞扬,又有对她的同情。读到这里,我们的耳边好像又响起了那深沉、幽怨的琵琶声!5、这首诗写的是昭君的怨恨,但首联一开始并没有写她的怨恨,写的是什么?这样写的目的又是什么?明确:群山万壑赴荆门山是群山起伏,连绵不绝;水是万壑争流,奔腾不息,直赴荆门山。其中的“赴”字用了拟人的手法,把迤逦不绝的千山万壑陡然间写活了,既有飞动之势,又有变幻之姿。从侧面烘托昭君的形象。两千多年前,一个青年女子远离父母之邦,嫁到异域,并在那里度过一生,确实需要巨大的勇气和毅力,而这雄伟的山川简直就是她那坚强的性格的象征。6、佳句鉴赏(这首诗歌当中,我认为有两句诗写得非常美,我自己很喜欢,不知道有没有同道中人?)

人教版高中语文必修3《杜甫诗三首 秋兴八首》教案2篇
4、主旨 哪一联明确地点明全诗题旨?表达了作者的什么感情?试做分析 颈联。 菊花开在秋天,所以这 “ 丛菊 ” 回应了诗题中那个 “ 秋 ” 字。 “ 他日 ” 可以指过去也可以指未来,在这里是指过去。“丛菊两开”,指诗人于 765 年离开成都,原打算很快出峡,但这年留居云安,次年又留居夔州,见到丛菊开了两次,还未出峡,故对菊掉泪。秋菊两度盛开,使诗人再次洒下往日流过的眼泪。“开”字双关,一谓菊花开,又言泪眼随之开。此时他仍然滞留在他乡,他始终没有放弃回乡的打算。孤舟可以系住,使其不能泛诸中流,但诗人的心是系不住的。他的心早已越过江河,越过关山,飞到了长安。所以,一叶靠岸系绳的孤舟,始终都牵动着诗人的故园之思。这一联是全篇诗意所在。孤舟本来只能系住自己的行踪,却把诗人的思乡之心也牢牢地系住了,故见舟伤心,引出故园之思,表现出思乡之情的深沉浓烈和欲归不得的无奈与凄伤,为文章的主旨句。

北师大初中七年级数学下册三角形的三边关系教案
方法总结:绝对值的化简首先要判断绝对值符号里面的式子的正负,然后根据绝对值的性质将绝对值的符号去掉,最后进行化简.此类问题就是根据三角形的三边关系,判断绝对值符号里面式子的正负,然后进行化简.三、板书设计1.三角形按边分类:有两边相等的三角形叫做等腰三角形,三边都相等的三角形是等边三角形,三边互不相等的三角形是不等边三角形.2.三角形中三边之间的关系:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既增加了学习兴趣,又增强了学生的动手能力

北师大初中八年级数学下册三角形的全等和等腰三角形的性质教案
证明:过点A作AF∥DE,交BC于点F.∵AE=AD,∴∠E=∠ADE.∵AF∥DE,∴∠E=∠BAF,∠FAC=∠ADE.∴∠BAF=∠FAC.又∵AB=AC,∴AF⊥BC.∵AF∥DE,∴DE⊥BC.方法总结:利用等腰三角形“三线合一”得出结论时,先必须已知一个条件,这个条件可以是等腰三角形底边上的高,可以是底边上的中线,也可以是顶角的平分线.解题时,一般要用到其中的两条线互相重合.三、板书设计1.全等三角形的判定和性质2.等腰三角形的性质:等边对等角3.三线合一:在等腰三角形的底边上的高、中线、顶角的平分线中,只要知道其中一个条件,就能得出另外的两个结论.本节课由于采用了动手操作以及讨论交流等教学方法,有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

人教版高中语文必修3《文学作品的个性化解读》教案2篇
教学目标:1、了解文学作品解读的个性化及其原因。2、探讨个性化解读遵循的基本原则,合理解读文学作品。教学重点:引导学生关注文学现象,培养他们对文学作品理解的多重思维能力。教学难点:把握个性化的度。避免偏激的理解、过度的张扬所谓个性,严重歪曲文学作品。教学方法:导读、计论、合作探究。教学时间:一课时教学过程:一、创设情境、揭题导入:记得有这样一个故事:一个小孩在四岁就能背《登鹳雀楼》,可平时只有在大人的要求下,他才背出来。直到六岁的某一天,他父母带他去旅游,在他登陆上山顶时,竟然随口背出:“欲穷千里目,更上一层楼”来。这说明了什么?……(讨论)文学作品解读的个性化。二、探讨个性化解读的原因1、读者的差异导致解读的个性化A、同一作品,阅读的时间不同,解读不同。如上面的例子。如《从百草园到三味书屋》和《风筝》主题的多元化理解。“温故知新”,名作重读,不但有趣,而且有益。B、同一作品,不同读者,解读不同。

人教版高中语文必修3《学会宽容 学习选择和使用论据》教案2篇
评价分析法,就是引述事例后,对所引述的事例作适当的评价,从而使自己的观点得到印证。例如,在论“节俭”时,引用了“曾国藩以俭戒子,其子曾纪泽终成出色的外交家;方志敏居官不贪,一生清贫,千古留名”的事实后,接着进行分析:是的,“俭者心常富”,节俭能培养人同困难作斗争的勇气和意志,而这正是一个人立业最重要的素质。从这个意义上说,有人说饥饿是人生的佐料,吃苦是一种资本也不无道理,而自觉和戒奢尚俭则更是促人修身养性,磨炼意志的有效途径。这里,作者紧扣论点,对论据进行了评价性分析,这种评价分析使作者的观点得到强化。(四)因果分析法因果分析法,就是抓住论据所述的事实,并据此推求形成原因的一种分析方法。事出必有其因。我们可以依据事物发展变化的因果关系,由事物发展变化的结果,推导出产生这种结果的原因,从而揭示出一定的生活规律,使事例有力地证明观点。

人教版高中语文必修3《一名物理学家的教育历程》教案
①阐发话题式:就是用简练的语言对所给话题材料加以概括和浓缩,并找到一个最佳切入点加以深层次阐述。吉林一考生的满分作文《漫谈“感情”“认知”》的题记是:“同是对‘修墙’‘防盗’的预见,却产生‘聪明’或‘被怀疑’的结果。‘感情’竟能如此地左右着‘认知’,心的小舟啊,在文化的河流中求索。”这个题记通过对材料的简单解释,将“感情”与“认知”二者的关系诠释得非常明白,也点明了作者的态度和议论的中心。②诠释题目式:所拟题目一般都具有深刻性特点,运用题记形式对题目进行巧妙而又全面的诠释。云南一考生的满分作文《与你同行》的题记是:“他们一路同行,一个汲着水,一个负着火,形影相随。在他们携手共进时,就产生了智慧。”这个题记形象而深刻地对“与你同行”这个题目进行了解释,言简意赅,表明了考生对感情和理智关系的认识。
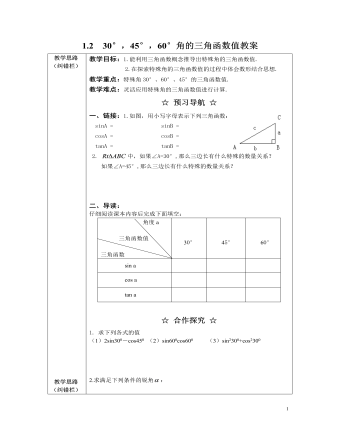
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中七年级数学下册利用“边角边”判定三角形全等教案
AD=CD,∠ADE=∠CDG,DE=GD,∴△ADE≌△CDG(SAS),∴AE=CG;(2)设AE与DG相交于M,AE与CG相交于N.在△GMN和△DME中,由(1)得∠CGD=∠AED,又∵∠GMN=∠DME,∠DEM+∠DME=90°,∴∠CGD+∠GMN=90°,∴∠GNM=90°,∴AE⊥CG.三、板书设计1.边角边:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.两边和其中一边的对角对应相等的两个三角形不一定全等.2.全等三角形判定与性质的综合运用本节课从操作探究入手,具有较强的操作性和直观性,有利于学生从直观上积累感性认识,从而有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边角边”掌握较好,但在探究三角形的大小、形状时不会正确分类,需要在今后的教学和作业中进一步加强分类思想的巩固和训练

北师大初中八年级数学下册等腰三角形的判定与反证法教案
方法总结:本题结合三角形内角和定理考查反证法,解此题关键要懂得反证法的意义及步骤.反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况.如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.三、板书设计1.等腰三角形的判定定理:有两个角相等的三角形是等腰三角形(等角对等边).2.反证法(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.解决几何证明题时,应结合图形,联想我们已学过的定义、公理、定理等知识,寻找结论成立所需要的条件.要特别注意的是,不要遗漏题目中的已知条件.解题时学会分析,可以采用执果索因(从结论出发,探寻结论成立所需的条件)的方法.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册利用三角函数测高2教案
问题2、如何用测角仪测量一个低处物体的俯角呢?和测量仰角的步骤是一样的,只不过测量俯角时,转动度盘,使度盘的直径对准低处的目标,记下此时铅垂线所指的度数,同样根据“同角的余角相等”,铅垂线所指的度数就是低处的俯角.活动三:测量底部可以到达的物体的高度.“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.要测旗杆MN的高度,可按下列步骤进行:(如下图)1.在测点A处安置测倾器(即测角仪),测得M的仰角∠MCE=α.2.量出测点A到物体底部N的水平距离AN=l.3.量出测倾器(即测角仪)的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).根据测量数据,就能求出物体MN的高度.在Rt△MEC中,∠MCE=α,AN=EC=l,所以tanα= ,即ME=tana·EC=l·tanα.又因为NE=AC=a,所以MN=ME+EN=l·tanα+a.

