-

中班语言课件教案:大象救小兔子
教学目标: 1、观察图片,讲述故事中角色对话。 2、懂得同伴之间应该相互关心、相互帮助的道理。 3、初步培养幼儿讲故事和表演故事的能力。 准备: 背景图一幅,小兔、大象、老虎(插入教具),头饰若干。。 过程: 一、进入主题。(音乐响起),带小朋友到树林里去玩玩。出示背景图。 二、演示教具,启发提问,引导幼儿讲述。 1、问:谁在小树林里?干什么?讨论后总结:小白兔、小灰兔、小黑兔在树林里高高兴兴地玩着。(学习词“高高兴兴”)。 2、插入老虎。哎呀!谁来了?它来干什么?小兔子们怎么办?总结:突然,从树林里窜出一只大老虎,它张着大大的嘴,露着尖尖的牙,要来抓小兔子,小兔子吓得转身就逃。(学习词“窜”)。

中班语言课件教案:贪吃水果的多多
2.能大胆创作,充分想象,用已掌握的搓、团圆、捏、压印等技能制作出各种水果,发展其动手能力。准备:1.泥巴若干,各种材料:树叶、牙签、小棒,树枝等。 2.泥蛇一条过程: 一、导入活动 1.(教师出示一条泥做的蛇)“你们看谁来了呀?” “它的名字叫多多。你们想知道多多的故事吗?” 二、欣赏故事 1.教师有表情的讲述故事,幼儿倾听。 2.提问:小蛇多多吃了哪些水果?

中班语言课件教案:米皮皮的“敲敲长”
2、能大胆于在集体面前说话。3、感受故事蕴含的幽默感,体验与同伴游戏的快乐。活动重点:理解故事内容,感受故事蕴含的幽默感,体验与同伴游戏的快乐。活动难点:练习发“Zhang”“SUO”的音。活动准备:米皮皮图片一幅,五彩小棍一根,米皮皮头饰一个,故事图片四张。活动过程:一、 欣赏故事:1、出示米皮皮图片。小朋友们看,今天,教师请来了一只小老鼠来我们班做客,嗯,它叫米皮皮,我们一起来向米皮皮问好吧!(米皮皮好!)“小朋友们好!”2、米皮皮还带来了一样宝贝,叫“敲敲长”。小朋友们跟老师一起来念念看(敲敲长)。3、米皮皮的敲敲长是一根五颜拥六色很漂亮的小棍,我们就叫它五彩小棍吧!“五彩小棍”我们一起说说看!

中班语言课件教案:耳朵上的绿星星
活动准备:1、制作课件《耳朵上的绿星星》、故事录音带;2、教具:小草、玫瑰花、萤火虫、星星头饰;小松鼠指偶等;3、画有小松鼠图像的画纸(与幼儿人数相等)、幼儿画笔若干。活动过程:一、提出疑问,导入课题孩子们,你们你!小朋友们好!(小松鼠)哦,是小松鼠来了,咦,小松鼠你的耳朵上怎么还有星星呀?星星不是在天上吗?这是怎么回事?小松鼠:听了下面的故事,你们就知道了!请听故事《耳朵上的绿星星》!二、教师有感情的讲述第一遍故事。孩子们,你们说这个故事名字叫什么?(〈耳朵上的绿星星〉)师:小松鼠,我们的孩子说得对吗?小松鼠:对!师:那么,萤火虫为什么跑到你的耳朵上呢?小松鼠:要回答这个问题,先请你们看看我带来的图片吧!师:哟,小松鼠还给我们带了好看的图片,让我们快来看吧。三、播放课件,请小朋友欣赏,教师讲述第二遍故事。1、播放第一部分a、小松鼠上台表演节目,他想怎样来打扮自己b、小松鼠打扮了吗?(没有)为什么c、这件事情让谁看到了?(萤火虫)萤火虫怎么说的?它为什么说小松鼠真好?d、小松鼠没有戴用草编成的帽子、也没有戴用花编成的项链,那他是怎样去参加音乐会呢?2、播放第二部分a、晚上,小松鼠是怎样参加音乐会的?b、是呀!小松鼠一点也没打扮,可是幕布一拉开,台下的观众都惊呆了,他们看到了什么?

中班语言课件教案:红圆圆和白团团
活动准备:1、情景布置:线的天地(各种各样的线)2、实物:红、白两种绒线团,一对棒针。用红、白两种绒线编织成的白底红十字图案的编织品。活动过程:一、参观“线的天地”,各种线的用途。二、出示红白两种绒线团,棒针,激发幼儿的兴趣。教师讲第一、二、三段故事,提问:1、故事里有谁?他们去干什么?2、红圆圆和白团团都说了些什么?讨论:红圆圆和白团团走但荒野,发生了什么事?(让幼儿想象,自由讨论)并让幼儿续编。三、教师讲完整个故事,提问:1、红圆圆和白团L'cd欧⑸氖赂忝墙驳氖遣皇且谎f2、她们在路上遇到什么?她们是怎么做的?3、最后,她们怎样了?4、我们听了这个故事,懂得了什道理?四、请幼儿分角色白哦眼并复述。五、师生小结:同伴之间应该互相帮忙、互相关心。

中班语言课件教案:故事创编表演
二、活动的由来: 三间房子搭建好之后,激起了孩子们表演的欲望,大家一起制作道具分配角色表演起来了,每个孩子在表演过程中都很投入,但发现孩子在选择角色时都喜欢扮演小花猪,由于大灰狼最后的遭遇不好,孩子都不喜欢扮演这个角色。有的孩子就提出问题:“大灰狼可不可以不死呀?”“大灰狼最后跟小猪成了好朋友”“大灰狼也很聪明,它也会想办法对付大灰狼的”。随着孩子们表演经验不断丰富,他们对故事的情节提出了新的要求,要求增加新的角色,于是,决定大家一起来改编故事并进行表演。三、活动具体目标:(1)创编故事并制订故事表演的计划,并能按计划去完成故事表演。(2)能运用语调、表情、动作去表现人物的形象和情感变化,发展幼儿的语感,增强语言的表现力。(3)通过表演游戏扩大词汇量,积累语言经验,在日常生活、交往中迁移运用,提高自身的语言能力。(4)培养幼儿自信、勇敢、大方的个性,能积极主动与人交谈、协商、合作与交往。

中班语言课件教案:故事《空气变新鲜了》
1、大森林与城市的背景图。 2、插入教具一套。四、设计思路: 环境保护是我国的基本国策之一。“环境教育”已走进中小学的课堂。作为基础教育的有机组成部分的幼儿教育,也有必要尽早让幼儿——21世纪的主人从小接受环境保护的启蒙教育。故事“空气变新鲜了”通过形象地描述了一只猴子从森林来到大城市,由于大城市的空气污染,而出现了身体上的一系列的不舒服,从而让幼儿知道造成空气污染的一些原因,更激发幼儿保护环境的意识,从小懂得保护环境,热爱自然。《纲要》中也指出,要让幼儿亲近自然,接触社会,初步了解人与环境的相互依存关系,有认识和探索的兴趣。五、流程设计: 创设情境,引出课题——>讲述故事,启发设问,讨论——>完整欣赏故事——>迁移 (一)、创设情境: 师:(出示城市背景图)有一只猴子,从森林来到大城市,小猴非常开心,它为什么很开心?) (二)、讲述故事、启发设问、讨论: 1、师讲述第一、二段。 提问:(1)、小猴为什么会得这种病?(辅:小猴在大森林里从来不生这种病) (2)、医生说最好的药是什么? 2、继续讲述。 提问:(1)、小猴会想什么办法让城市里的那些人也吸到森林的空气? (2)、生病的那些人想怎么样让城里的空气也变新鲜? (启发幼儿讨论,想各种办法) (辅:大烟囱冒烟怎么办?汽车后面排出的尾气有毒怎么办?城里的人还是这么拥挤怎么办?) (三)、完整讲述: 师:城里的人到底怎样让空气变新鲜呢?让我们来完整听一遍。 (四)、迁移: 师:大家让城里的空气变得清清的、香香的,生活在这样的环境里,大家生活愉快,身体一定也 会更好。现在,我们一起到幼儿园找找,看看哪些地方还可以添些什么?怎样使我们幼儿园的空气更新鲜、更美丽。

中班语言课件教案:怪脾气的小乌龟
2、引导幼儿理解故事内容,能和老师一起讲述故事。活动准备:乌龟、蜗牛、请问的木偶各一个,3组图画活动重点:愿意表达自己的感受,能和老师一起讲述故事。活动过程:一、开始部分:1. 律动引入,邀请幼儿观看木偶表演。2. 情景导入:(1)通过木偶剧的名字“怪脾气的小乌龟”引起幼儿观看的兴趣。老师有表情的提出问题:小乌龟为什么是怪脾气?(2)通过入场须知,让幼儿了解看木偶剧的时候应该怎样做。

中班社会教案:自己被别人打了怎么办
二、活动目的: 1.教育幼儿在日常生活中应怎样与人相处。 2.教育幼儿能选择一种处理问题的较好的方式方法。 3.学习初步简单的分析问题。 三、重点难点分析: 重点:教育幼儿在日常生活中应怎样与人相处。 难点:学习初步简单的分析问题,教育幼儿选择一种处理问题的较好的方式方法。 四、活动准备:看录像 五、活动过程: (一)导入 组织幼儿看一段录像。 两个小朋友在玩一盒玩具,玩着玩着,他们同时发现了一件新玩具。为此吵了起来,后来又动手相互打对方。

中班健康:人体的支架骨骼课件教案
2、懂得用多种方法保护骨骼,养成良好的行为习惯,促进骨骼的生长发育。 二、活动准备:动物骨头:鱼骨头、肉骨头;骨骼支架图一幅;操作卡若干;录音机、磁带、投影仪、笔等。三、活动过程: (一)以动物骨骼引起幼儿兴趣。(二)了解人体的支架——骨骼。 1、找找说说哪儿有骨骼?它是怎样的?2、结合图片共同整理,了解人体骨骼的数量和有关名称。3、体验了解骨骼的作用。

中班社会:拾到东西还给别人课件教案
2、引导幼儿体验丢失东西和捡到东西后的着急心情,找到东西和把东西还给别人时的不同情绪情感。准备:动物头饰情景表演过程:开始部分(一)引起兴趣,引出课题。 师:今天,老师要来变个魔术,你们想看吗?(二)基本部分:1、情景表演,让幼儿了解小猫丢了东西着急、难过的心情和小兔把东西还给它以后高兴的心情。提问: 1、小猫丢了什么?心里怎么样?(着急、难过)2、谁捡到了帽子? (小兔)3、小兔捡到了帽子是怎么做的? (他说了什么?)集体练习: 请问,这是你丢的帽子吗?小结: 把帽子还给了小猫,小猫可高兴了,小兔着见小猫这么高兴,他心理也很高兴,我们小朋友要向小兔学习,拾到东西要还给别人。2、讨论,帮助幼儿体验丢了东西、拾到东西还给别人等情况下的不同情感。(1)小朋友有没有无过东西? 丢过什么? 心里怎样?(2)你丢了东西,别人拾了还给你,你心里怎样?(3)你有没有拾到过别人的东西? 你是怎么做的? 心里怎么样?

北师大初中数学八年级上册三角形的外角1教案
探究点二:三角形内角和定理的推论2如图,P是△ABC内的一点,求证:∠BPC>∠A.解析:由题意无法直接得出∠BPC>∠A,延长BP交AC于D,就能得到∠BPC>∠PDC,∠PDC>∠A.即可得证.证明:延长BP交AC于D,∵∠BPC是△ABC的外角(外角定义),∴∠BPC>∠PDC(三角形的一个外角大于任何一个和它不相邻的内角).同理可证:∠PDC>∠A,∴∠BPC>∠A.方法总结:利用推论2证明角的大小时,两个角应是同一个三角形的内角和外角.若不是,就需借助中间量转化求证.三、板书设计三角形的外角外角:三角形的一边与另一边的延长线所组成的 角,叫做三角形的外角推论1:三角形的一个外角等于和它不相邻的两 个内角的和推论2:三角形的一个外角大于任何一个和它不 相邻的内角利用已经学过的知识来推导出新的定理以及运用新的定理解决相关问题,进一步熟悉和掌握证明的步骤、格式、方法、技巧.进一步培养学生的逻辑思维能力和推理能力,特别是培养有条理的想象和探索能力,从而做到强化基础,激发学习兴趣.

北师大初中数学八年级上册一定是直角三角形吗1教案
方法总结:利用三角形三边的数量关系来判定直角三角形,从而推出两线的垂直关系.探究点二:勾股数下列几组数中是勾股数的是________(填序号).①32,42,52;②9,40,41;③13,14,15;④0.9,1.2,1.5.解析:第①组不符合勾股数的定义,不是勾股数;第③④组不是正整数,不是勾股数;只有第②组的9,40,41是勾股数.故填②.方法总结:判断勾股数的方法:必须满足两个条件:一要符合等式a2+b2=c2;二要都是正整数.三、板书设计勾股定理的逆定理: 如果一个三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.勾股数:满足a2+b2=c2的三个正整数,称为勾股数.经历一般规律的探索过程,发展学生的抽象思维能力、归纳能力.体验生活中数学的应用价值,感受数学与人类生活的密切联系,激发学生学数学、用数学的兴趣.

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中数学九年级上册利用两角判定三角形相似1教案
解:方法一:因为DE∥BC,所以∠ADE=∠B,∠AED=∠C,所以△ADE∽△ABC,所以ADAB=DEBC,即44+8=5BC,所以BC=15cm.又因为DF∥AC,所以四边形DFCE是平行四边形,所以FC=DE=5cm,所以BF=BC-FC=15-5=10(cm).方法二:因为DE∥BC,所以∠ADE=∠B.又因为DF∥AC,所以∠A=∠BDF,所以△ADE∽△DBF,所以ADDB=DEBF,即48=5BF,所以BF=10cm.方法总结:求线段的长,常通过找三角形相似得到成比例线段而求得,因此选择哪两个三角形就成了解题的关键,这就需要通过已知的线段和所求的线段分析得到.三、板书设计(1)相似三角形的定义:三角分别相等、三边成比例的两个三角形叫做相似三角形;(2)相似三角形的判定定理1:两角分别相等的两个三角形相似.感受相似三角形与相似多边形、相似三角形与全等三角形的区别与联系,体验事物间特殊与一般的关系.让学生经历从实验探究到归纳证明的过程,发展学生的合情推理能力,培养学生的观察、动手探究、归纳总结的能力.

大班社会教案给予和接受称赞
1 教育幼儿要学会接受称赞,大大方方接受后,说声谢谢。2 丰富一些词汇。活动准备:挂图。活动过程:教师讲述故事:在一座美丽的森林里,有一只可爱的小黄莺,它唱歌唱得非常好听。有一天,森林里开音乐会,小动物们请小黄莺去唱歌。森林音乐会开始了,大家表演的节目可真好。小青蛙拉的小提琴、小麻雀的小合唱团。最后一个节目轮到小黄莺上台,主持人狐狸小姐说:请咱们的歌唱家小黄莺唱一支,它唱的歌可动听了。动物们的目光一下子朝小黄莺看去,小黄莺不好意思的低下了头,红着脸上了台。开始唱歌,可是歌没唱一半,声音就小得几乎听不见,。动物们说?小黄莺的声音太小了。听到动物们的话,歌没唱完就飞走了。回到家里,它把这件事情告诉了妈妈,妈妈听完,微笑着对她说……

大班社会教案:给予和接受称赞
1、教育幼儿要学会接受称赞,大大方方接受后,说声谢谢。2、丰富一些词汇。活动准备:挂图。活动过程 教师讲述故事:在一座美丽的森林里,有一只可爱的小黄莺,它唱歌唱得非常好听。有一天,森林里开音乐会,小动物们请小黄莺去唱歌。森林音乐会开始了,大家表演的节目可真好。小青蛙拉的小提琴、小麻雀的小合唱团。最后一个节目轮到小黄莺上台,主持人狐狸小姐说:请咱们的歌唱家小黄莺唱一支,它唱的歌可动听了。动物们的目光一下子朝小黄莺看去,小黄莺不好意思的低下了头,红着脸上了台。开始唱歌,可是歌没唱一半,声音就小得几乎听不见,。动物们说?小黄莺的声音太小了。听到动物们的话,歌没唱完就飞走了。回到家里,它把这件事情告诉了妈妈,妈妈听完,微笑着对她说……

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业
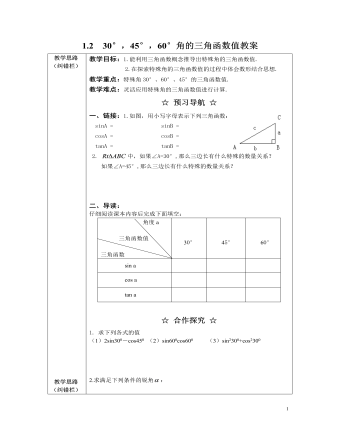
北师大初中九年级数学下册30°,45°,60°角的三角函数值2教案
教学目标:1.能利用三角函数概念推导出特殊角的三角函数值.2.在探索特殊角的三角函数值的过程中体会数形结合思想.教学重点:特殊角30°、60°、45°的三角函数值.教学难点:灵活应用特殊角的三角函数值进行计算.☆ 预习导航 ☆一、链接:1.如图,用小写字母表示下列三角函数:sinA = sinB =cosA = cosB =tanA = tanB =2. 中,如果∠A=30°,那么三边长有什么特殊的数量关系?如果∠A=45°,那么三边长有什么特殊的数量关系?二、导读:仔细阅读课本内容后完成下面填空:

北师大初中数学八年级上册三角形的外角2教案
证法二:(1)延长BD交AC于E(或延长CD交AB于E),如图.则∠BDC是△CDE的一个外角.∴∠BDC>∠DEC.(三角形的一个外角大于任何一个和它不相邻的内角)∵∠DEC是△ABE的一个外角(已作)∴∠DEC>∠A(三角形的一个外角大于任何一个和它不相邻的内角)∴∠BDC>∠A(不等式的性质)(2)延长BD交AC于E,则∠BDC是△DCE的一个外角.∴∠BDC=∠C+∠DEC(三角形的一个外角等于和它不相邻的两个内角的和)∵∠DEC是△ABE的一个外角∴∠DEC=∠A+∠B(三角形的一个外角等于和它不相邻的两个内角的和)∴∠BDC=∠B+∠C+∠BAC(等量代换)活动目的:让学生接触各种类型的几何证明题,提高逻辑推理能力,培养学生的证明思路,特别是不等关系的证明题,因为学生接触较少,因此更需要加强练习.注意事项:学生对于几何图形中的不等关系的证明比较陌生,因此有必要在证明第2小题中,要引导学生找到一个过渡角∠ACB,由∠1>∠ACB,∠ACB>∠2,再由不等关系的传递性得出∠1>∠2。

