-

北师大初中数学九年级上册反比例函数的应用1教案
因为反比例函数的图象经过点A(1.5,400),所以有k=600.所以反比例函数的关系式为p=600S(S>0);(2)当S=0.2时,p=6000.2=3000,即压强是3000Pa;(3)由题意知600S≤6000,所以S≥0.1,即木板面积至少要有0.1m2.方法总结:本题渗透了物理学中压强、压力与受力面积之间的关系p= ,当压力F一定时,p与S成反比例.另外,利用反比例函数的知识解决实际问题时,要善于发现实际问题中变量之间的关系,从而进一步建立反比例函数模型.三、板书设计反比例函数的应用实际问题与反比例函数反比例函数与其他学科知识的综合经历分析实际问题中变量之间的关系,建立反比例函数模型,进而解决问题的过程,提高运用代数方法解决问题的能力,体会数学与现实生活的紧密联系,增强应用意识.通过反比例函数在其他学科中的运用,体验学科整合思想.
北师大初中数学九年级上册概率与游戏的综合运用2教案
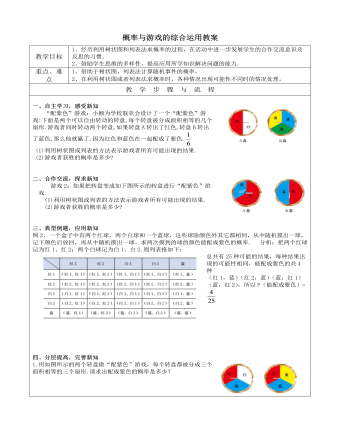
三、典型例题,应用新知例2、一个盒子中有两个红球,两个白球和一个蓝球,这些球除颜色外其它都相同,从中随机摸出一球,记下颜色后放回,再从中随机摸出一球。求两次摸到的球的颜色能配成紫色的概率. 分析:把两个红球记为红1、红2;两个白球记为白1、白2.则列表格如下:总共有25种可能的结果,每种结果出现的可能性相同,能配成紫色的共4种(红1,蓝)(红2,蓝)(蓝,红1)(蓝,红2),所以P(能配成紫色)= 四、分层提高,完善新知1.用如图所示的两个转盘做“配紫色”游戏,每个转盘都被分成三个面积相等的三个扇形.请求出配成紫色的概率是多少?2.设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为 五、课堂小结,回顾新知1. 利用树状图和列表法求概率时应注意什么?2. 你还有哪些收获和疑惑?

北师大初中八年级数学下册一元一次不等式组的解法教案
把解集在数轴上表示出来,并将解集中的整数解写出来.解析:分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集,再找出解集范围内的整数即可.解:x+23<1 ①,2(1-x)≤5 ②,由①得x<1,由②得x≥-32,∴不等式组的解集为-32≤x<1.则不等式组的整数解为-1,0.方法总结:此题主要考查了一元一次不等式组的解法,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件进而求得不等式组的整数解.三、板书设计一元一次不等式组概念解法不等式组的解集利用数轴确定解集利用口诀确定解集解一元一次不等式组是建立在解一元一次不等式的基础之上.解不等式组时,先解每一个不等式,再确定各个不等式组的解集的公共部分.

北师大初中数学九年级上册反比例函数的图象2教案
观察 和 的图象,它们有什么相同点和不同点?学生小组讨论,弄清上述两个图象的异同点。交流讨论反比 例函数图象是中心对称图形吗?如果是,请找出对称中心.反比例函数图象是轴对称图形吗?如果是,请指出它的对称轴.二、随堂练习课本随堂练习 [探索与交流]对于函数 , 两支曲线分别位于哪个象限内?对于函数 ,两支曲线又分别位于哪个象限内?怎样区别这两个函数的图象。学生分四人小组全班探索。 三、课堂总结在进行函数的列表,描点作图的活动中,就已经渗透了反比例函数图象的特征,因此在作图象的过程中,大家要进行积极的探索 。另外,(1)反比例函数的图象是非线性的,它的图象是双曲线;(2)反比例 函数y= 的图像,当k>0时,它的图像位于一、三象限内,当k<0时,它的图像位于二、四象限内;(3)反比例函数既是中心对称图形,又是轴对称图形。

北师大初中八年级数学下册异分母分式的加减教案
分式1x2-3x与2x2-9的最简公分母是________.解析:∵x2-3x=x(x-3),x2-9=(x+3)(x-3),∴最简公分母为x(x+3)(x-3).方法总结:最简公分母的确定:最简公分母的系数,取各个分母的系数的最小公倍数;字母及式子取各分母中所有字母和式子的最高次幂.“所有字母和式子的最高次幂”是指“凡出现的字母(或含字母的式子)为底数的幂的因式选取指数最大的”;当分母是多项式时,一般应先因式分解.【类型二】 分母是单项式分式的通分通分.(1)cbd,ac2b2;(2)b2a2c,2a3bc2;(3)45y2z,310xy2,5-2xz2.解析:先确定最简公分母,找到各个分母应当乘的单项式,分子也相应地乘以这个单项式.解:(1)最简公分母是2b2d,cbd=2bc2b2d,ac2b2=acd2b2d;(2)最简公分母是6a2bc2,b2a2c=3b2c6a2bc2,2a3bc2=4a36a2bc2;(3)最简公分母是10xy2z2,45y2z=8xz10xy2z2,310xy2=3z210xy2z2,5-2xz2=--25y210xy2z2.

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中九年级数学下册弧长及扇形的面积教案
1.了解扇形的概念,理解n°的圆心角所对的弧长和扇形面积的计算公式并熟练掌握它们的应用;(重点)2.通过复习圆的周长、圆的面积公式,探索n°的圆心角所对的弧长l=nπR180和扇形面积S扇=nπR2360的计算公式,并应用这些公式解决一些问题.(难点)一、情境导入如图是圆弧形状的铁轨示意图,其中铁轨的半径为100米,圆心角为90°.你能求出这段铁轨的长度吗(π 取3.14)?我们容易看出这段铁轨是圆周长的14,所以铁轨的长度l≈2×3.14×1004=157(米). 如果圆心角是任意的角度,如何计算它所对的弧长呢?二、合作探究探究点一:弧长公式【类型一】 求弧长如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为()

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

北师大初中九年级数学下册三角函数的计算2教案
解在角度单位状态为“度”的情况下(屏幕显示出 ),按下列顺序依次按键:显示结果为36.538 445 77.再按键:显示结果为36゜32′18.4.所以,x≈36゜32′.例5 已知cot x=0.1950,求锐角x.(精确到1′)分析根据tan x= ,可以求出tan x的值,然后根据例4的方法就可以求出锐角x的值.四、课堂练习1. 使用计算器求下列三角函数值.(精确到0.0001)sin24゜,cos51゜42′20″,tan70゜21′,cot70゜.2. 已知锐角a的三角函数值,使用计算器求锐角a.(精确到1′)(1)sin a=0.2476; (2)cos a=0.4174;(3)tan a=0.1890; (4)cot a=1.3773.五、学习小结内容总结不同计算器操作不同,按键定义也不一样。同一锐角的正切值与余切值互为倒数。在生活中运用计算器一定要注意计算器说明书的保管与使用。方法归纳在解决直角三角形的相关问题时,常常使用计算器帮助我们处理比较复杂的计算。

北师大初中九年级数学下册三角函数的应用1教案
然后,她沿着坡度是i=1∶1(即tan∠CED=1)的斜坡步行15分钟抵达C处,此时,测得A点的俯角是15°.已知小丽的步行速度是18米/分,图中点A、B、E、D、C在同一平面内,且点D、E、B在同一水平直线上.求出娱乐场地所在山坡AE的长度(参考数据:2≈1.41,结果精确到0.1米).解析:作辅助线EF⊥AC于点F,根据速度乘以时间得出CE的长度,通过坡度得到∠ECF=30°,通过平角减去其他角从而得到∠AEF=45°,即可求出AE的长度.解:作EF⊥AC于点F,根据题意,得CE=18×15=270(米). ∵tan∠CED=1,∴∠CED=∠DCE=45°.∵∠ECF=90°-45°-15°=30°,∴EF=12CE=135米.∵∠CEF=60°,∠AEB=30°,∴∠AEF=180°-45°-60°-30°=45°,∴AE=2EF=1352≈190.4(米).所以,娱乐场地所在山坡AE的长度约为190.4米.方法总结:解决本题的关键是能借助仰角、俯角和坡度构造直角三角形,并结合图形利用三角函数解直角三角形.

北师大初中九年级数学下册图形面积的最大值1教案
如图所示,要用长20m的铁栏杆,围成一个一面靠墙的长方形花圃,怎么围才能使围成的花圃的面积最大?如果花圃垂直于墙的一边长为xm,花圃的面积为ym2,那么y=x(20-2x).试问:x为何值时,才能使y的值最大?二、合作探究探究点一:二次函数y=ax2+bx+c的最值已知二次函数y=ax2+4x+a-1的最小值为2,则a的值为()A.3 B.-1 C.4 D.4或-1解析:∵二次函数y=ax2+4x+a-1有最小值2,∴a>0,y最小值=4ac-b24a=4a(a-1)-424a=2,整理,得a2-3a-4=0,解得a=-1或4.∵a>0,∴a=4.故选C.方法总结:求二次函数的最大(小)值有三种方法,第一种是由图象直接得出,第二种是配方法,第三种是公式法.变式训练:见《学练优》本课时练习“课堂达标训练” 第1题探究点二:利用二次函数求图形面积的最大值【类型一】 利用二次函数求矩形面积的最大值

大班健康教育活动:身体的秘密教案
在本月开展多元智能创意课程《变变变,长大了》主题活动时,有一个分题活动是“身体的秘密”,孩子们一看到书中男女小朋友入厕的情景,立即炸开了锅。同时,他们对两性问题表现出的早熟倾向引起了我们的关注:有的孩子在课后扭住我提了很多他关于成人生活的困惑;还有的男孩子竟忍不住好奇,偷偷跑进女厕所想一窥究竟……(略)于是,我们决定对孩子们现阶段最为关注的话题作出正面的、积极的回应,同时对学前教育阶段如何开展启蒙“性教育”进行探索,生成了本次活动“身体的秘密”。活动目标:1、科学、正确地面对性话题,学会尊重自己和别人的身体。2、有初步的自我保护意识,了解基本的防卫方法。3、引导幼儿积极地思维,自由地表达。活动准备:1、幼儿的准备:活动前的调查记录,对两性的区别有了初步的认识;2、教师的准备:l 搜集大量的性教育资料(今日说法、《画说性》等),以应对课堂上孩子们的突发提问;l 角色分工、互助协调; 布置有关两性知识的活动区角(包括人物、动物),提供较为丰富安全的可操作材料。活动过程: 一、谈话引入,讲解什么是“性”。1、请小朋友以性别分为男女两组,两名老师明确分工。幼儿阐述自己对不同性别的看法,即“男女有什么区别”。2、提问引发思考:什么是“性”?小结:“性”是和我们的身体密切相关的,不关是从头发的长短就能判断性别的,更重要的是我们身体的某些部位,是代表着性别差异的。是那些部位呢?就是我们穿衣服遮起来的部位。

20以内的不退位减法教案教学设计
教学目标:1.引导幼儿参与学习活动,经历十几减几计算方法的探索与算理的建构过程。2.根据 11 至 20 各数的组成,掌握 20 以内不进位加法和不进位减法的计算方法。教学重点:十几减几(不退位)的计算。教学过程:一、复习导入复习10以内的数的组合,11~20各数的组成。1.碰球游戏导入,复习10的分解组合2.老师分别出示数字卡片:14、17、12、11。幼儿说数的组成。

大班健康:认识常见的安全标记教案
2、通过寻找生活中的安全标记,了解生活中的安全标记和人的生命安全有着密切的联系。3、在制作安全标记的过程中,加强对安全标记的认识,培养一定的安全意识。活动准备:1、常见的安全标记图;红、绿灯;禁止吸烟;禁止攀爬;禁止通行等。2、幼儿用书人手一册。活动过程:1、教师出示红、绿灯的安全标记图,引导幼儿观察:这是什么,你在什么地方见到过这些标记?这个标记告诉我们什么?然后分别出示其它标记,引导幼儿认识具体方法同上。

幼儿园大班健康教案:牙齿上的洞洞
活动准备: 1、鸡蛋壳、饼干、杯子、醋、镜子 2、课前两天和幼儿一起将鸡蛋壳浸在醋里; 3、产生龋齿的过程图片和牙防五步曲的图片 4、牙模型、牙刷各一、动画片《聪聪王子牙防历险记》活动过程: 一、律动进场,引出情景表演; 牙宝宝在哭,原来是他的小主人喜欢吃甜食,又不刷牙,时间长了,细菌在牙宝宝的身上钻了几个洞洞。

大班健康:身体的哪些部位可以动教案
2、激发幼儿敢于探索和勇于发现的学习兴趣,培养幼儿互相合作,互相谦让的优良品质。 活动准备:音乐 活动过程: 一、游戏《木头人》,指出人不动是很难受的。 二、让幼儿明白人有各种各样的活动,是因为人的许多部位都可以动。 1、听音乐做动作 提问:刚才,我们跟着音乐在干什么?是身体的哪些部位跟着音乐在动? 2、引导幼儿观察周围生活 提问:除了舞蹈是人身体的一种活动外,你还知道人们有些什么样的活动?它们分别是我们身体的哪些部位在动?

幼儿园大班韵律教案:快乐的阿依古丽
2、按舞蹈情节记忆动作顺序。 3、初步体验新疆舞蹈的欢快与民族特色。 活动准备: 1、新疆娃娃或新疆帽一顶。 2、人手一件打击乐器。 活动过程: 1、在《水果丰收》乐曲伴奏下,复习踵趾步及摘果子等动作。 2、了解《葡萄丰收》舞蹈情节。 (1)教师出示新疆娃娃或新疆帽,幼儿观察并说出这是新疆小朋友以及新疆人最爱跳舞的特点。 (2)教师讲解舞蹈情节。 3、学跳舞蹈。 (1)教师示范,幼儿欣赏。 (2)教师再次舞蹈,幼儿观察并说出老师跳了些什么动作。 (3)先练习“手”的动作。在座位上坐着做、站起来站在椅子前面做。 (4)重点练习踮步与进退步。 (5)教师边说故事情节,边示范舞蹈,幼儿跟着老师学习舞蹈。 (6)重点练习在学习过程中有困难的动作,在继续完整练习舞蹈。 (7)教师或一些幼儿戴新疆帽舞蹈,其余幼儿欣赏并拍手伴奏,体验新疆帽舞蹈的欢快情绪和民族特色。

幼儿园大班音乐舞蹈教案《会跳舞的彩纸》
孩子到了大班,有了一定的“舞”的艺术表现能力。对音乐的感受力、想象力有了较大地提高,动手操作能力也在不断完善。特别喜欢自己探索、创造,并有一定的表演欲望。因此,我根据大班孩子的特点设计了这个以幼儿舞蹈为主的综合艺术活动。活动融合了手工、动作、舞蹈、即兴创编、画舞谱,还有本民族音乐、舞蹈的学习和体验的内容。对于大班的孩子,不要求舞姿,只要通过探索-发现、操作-尝试、感受-体验、即兴-创作等活动来品味“舞”的愉悦。 安排的活动流程为:准备活动——探索、发现——结伴创编——展现欣赏一、活动目标: 1、探索发现:彩纸表现的可能性,尝试“画”简单的舞谱。 2、提高身体协调能力,对合作表演产生兴趣。 3、体验飘逸和“舞”的愉悦。二、材料及环境设计: 1、录有欢快本民族音乐的磁带一盘。 2、彩色皱纹纸、竹筷若干。 3、小脚图谱、小剪刀、胶布等。 4、为幼儿提供能自由活动的较宽松的空间。

幼儿园大班美术教案:神奇的海底世界
活动准备: 1、已经绘画过海洋中的生物的造型和特征。 2、带有波浪版画的范图。 3、各色颜料、吹塑纸。 活动过程: 一、幼儿迁移经验,回忆海洋中的生物。 师:“小朋友我们知道海洋是什么样了?” (让幼儿根据自己的经验进行回答,教师提醒幼儿较完整地表达自己的意思,并说说不同生物的样子。) 幼儿尝试设计自己的潜艇或潜水服。

