-

幼儿园大班综合说课稿 魔术师
今天我说课的内容是大班综合活动《魔术师》。这个活动将语言与绘画整合。诗歌富有童趣,具有丰富的想象,各种颜色变出的物体是幼儿日常生活中常见的事物。教材来源于幼儿的生活。为此我选择这个教材,尝试将诗歌与绘画结合,使幼儿多通道的参与。活动的目标是教育活动的起点和归宿,对活动起着导向作用。依据《纲要》中“引导幼儿接触优秀的儿童文学作品,使之感受语言的丰富和优美,并通过多种活动帮助幼儿加深对作品的体验和理解”的要求及大班幼儿年龄特点,我制定了2个教育目标:1、帮助幼儿理解诗歌的内容和表现形式,使幼儿喜欢朗诵儿歌。2、感受生活中丰富多彩的颜色,能大胆想象用画笔表现并根据自己画的内容进行仿编诗歌。本次活动的重点是理解诗歌的内容和表现形式并学会朗诵。难点是用画笔表现生活中丰富的色彩并进行自己画的内容仿编诗歌。

幼儿园大班健康说课稿:心情播报
新《纲要》中指出:“幼儿身体的健康和心理的健康是密切相关的,要高度重视良好人际环境对幼儿身心健康的重要性。”由于现在的孩子大多都是独生子女,在家中是小皇帝,非常受宠,所以当遇到不开心的事时,就会乱发脾气,不会调节自己的心情,也不会照顾他人的情绪,更不懂得如何让自己快乐,并带给他人快乐。因此,设计了这次以幼儿心理健康教育为目的的活动:《心情播报》。 活动以幼儿感兴趣的节目主持人选拔赛为主线,使幼儿在“玩中学,学中乐”,最后达到以下目标: 1、使幼儿懂得理解他人的情绪情感。 2、并学会用各种方法让他人和自己高兴。 3、发展幼儿的想象力及大胆表述的能力。 根据目标,我把活动重点定位于让幼儿知道每个人的心情都有晴天和雨天的时候。把难点定位于让幼儿知道可以用什么方法让他人和自己的心情变成晴天。

幼儿园大班主题说课稿 鸟的家族
“鸟”是动物世界中的一个大的家族。在厦门,到处都可以看到鸟的身影、听到鸟的叫声。而且教育的资源也很丰富:家庭养鸟、花鸟市场、公园,厦门的白鹭洲有鸽子,鼓浪屿上有“百鸟园”等。大班的孩子对鸟的认识有一定的经验,他们喜欢给鸟喂食,还喜欢亲近鸟。这些鸟有着不同的外表,不同的生活习性,不同的生活环境,对人类有不同的作用。那么多的鸟也有相同的特征:有羽毛,有翅膀、会飞……。新《纲要》告诉我们,“要与社区密切合作、综合利用各种教育资源,共同为幼儿的发展创造良好的条件。”因此,我认为,引导幼儿进一步探索鸟与人类的关系,探索不同鸟类的不同的生活环境有着一定的教育价值。 2.目标定位:活动目标是教育活动的起点和归宿,对活动起着导向的作用。依据大班幼儿的年龄特点和教材本身的特点,我从情感态度、能力、认知等方面确定了本次活动的目标,其中既有独立表达的成分,又有相互融和的一面。

幼儿园大班语言说课稿《彩色的雨》
1、教材分析 《彩色的雨》是一首优美动听、充满童真童趣的散文,它运用了比喻、排比、等修辞手法,描写了娃娃心中彩色的雨。散文中形象的把小雨点比喻成亮晶晶的象一粒粒透明的珠子,那黄色的、蓝色的雨衣,象一片片彩色的云,那绿色的、紫色的伞儿象一朵朵彩色的花,那一双双红雨鞋象一艘艘小红船,这些生动的比喻构成了一组组排比句,增添了散文的韵律美。同时,散文中把构成彩色的雨的雨衣、伞儿、红雨鞋在雨中的动态都描绘的有声有色,作品不仅画面感强,想象丰富,而且语言凝练,韵律和谐,有较强的音乐性,即乐意躺幼儿欣赏彩色的雨的美丽景色,又可以让幼儿欣赏散文的意境美、语言美,在这同时又能激发幼儿动手制作彩色的雨的强烈愿望,因此这篇《彩色的雨》适合大班幼儿进行教学。

《巧儿我自幼儿许配赵家》教案
《巧儿我自幼儿许配赵家》这段曾经风靡全国的唱腔采用的是“喇叭牌子”。传统中这个曲牌用唢呐伴奏,唱词虚词衬字多,曲调简单粗糙。 初排《刘巧儿》时这段唱曾遭到非议,徐文华在几种板式都不理想的情况下,提议用这个曲牌,节奏跳跃灵活,但由于旧评剧中此调比较庸俗,所以要推陈出新。 经改革后的这段“小桥送线”,其前半段,伴奏乐器中去掉唢呐,改为弦乐,细腻传情;过门也变化得长短灵活;演唱时也去掉不必要的衬字;后半部有数板,半说半唱,用高低木鱼和三弦衬托;最后几句对桥下景色的描绘与人物此时的心境融合起来,传神传情。

北师大初中数学九年级上册正方形的性质1教案
在Rt△ABC中,AC=AB2+BC2=12+12=2(cm),∴FC=AC-AF=2-1(cm),∴BE=2-1(cm).方法总结:正方形被对角线分成4个等腰直角三角形,因此在正方形中解决问题时常用到等腰三角形的性质与直角三角形的性质.【类型三】 利用正方形的性质证明线段相等如图,已知过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.解析:由PE⊥BC,PF⊥CD知四边形PECF为矩形,故有EF=PC,这时只需说明AP=CP,由正方形对角线互相垂直平分可知AP=CP.证明:连接AC,PC,如图.∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.方法总结:(1)在正方形中,常利用对角线互相垂直平分证明线段相等;(2)无论是正方形还是矩形,经常连接对角线,这样可以使分散的条件集中.

北师大初中七年级数学上册多边形和圆的初步认识教案2
1、 如图4-25,将一个圆分成三个大小相同的扇形,你能算出它们的圆心角的度数吗?你知道每个扇形的面积和整个圆的面积的关系吗?与同伴进行交流2、 画一个半径是2cm的圆,并在其中画一个圆心为60º的扇形,你会计算这个扇形的面积吗?与同伴交流。教师对答案进行汇总,讲解本题解题思路:1、 因为一个圆被分成了大小相同的扇形,所以每个扇形的圆心角相同,又因为圆周角是360º,所以每个扇形的圆心角是360º÷3=120º,每个扇形的面积为整个圆的面积的三分之一。2、 先求出这个圆的面积S=πR²=4π,60÷360=1/6扇形面积=4π×1/6=2π/3【设计意图】运用小组合作交流的方式,既培养了学生的合作意识和能力,又达到了互帮互助以弱带强的目的,使学习比较吃力的同学也能参与到学习中来,体现了学生是学习的主体。

北师大初中七年级数学下册等腰三角形的性质教案
方法总结:在等腰三角形有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.三、板书设计1.等腰三角形的性质:等腰三角形是轴对称图形;等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴;等腰三角形的两个底角相等.2.运用等腰三角性质解题的一般思想方法:方程思想、整体思想和转化思想.本节课由于采用了直观操作以及讨论交流等教学方法,从而有效地增强了学生的感性认识,提高了学生对新知识的理解与感悟,因而本节课的教学效果较好,学生对所学的新知识掌握较好,达到了教学的目的.不足之处是少数学生对等腰三角形的“三线合一”性质理解不透彻,还需要在今后的教学和作业中进一步巩固和提高

北师大初中七年级数学下册利用“边边边”判定三角形全等教案
解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n边形的一个顶点可以作(n-3)条对角线,把多边形分成(n-2)个三角形,所以,要使一个n边形木架不变形,至少需要(n-3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.三、板书设计1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”.2.三角形的稳定性本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练

北师大初中七年级数学下册利用“边角边”判定三角形全等教案
AD=CD,∠ADE=∠CDG,DE=GD,∴△ADE≌△CDG(SAS),∴AE=CG;(2)设AE与DG相交于M,AE与CG相交于N.在△GMN和△DME中,由(1)得∠CGD=∠AED,又∵∠GMN=∠DME,∠DEM+∠DME=90°,∴∠CGD+∠GMN=90°,∴∠GNM=90°,∴AE⊥CG.三、板书设计1.边角边:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.两边和其中一边的对角对应相等的两个三角形不一定全等.2.全等三角形判定与性质的综合运用本节课从操作探究入手,具有较强的操作性和直观性,有利于学生从直观上积累感性认识,从而有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边角边”掌握较好,但在探究三角形的大小、形状时不会正确分类,需要在今后的教学和作业中进一步加强分类思想的巩固和训练

北师大初中数学九年级上册相似三角形判定定理的证明1教案
当Δ=l2-4mn<0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的一个点P;当Δ=l2-4mn=0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的两个点P;当Δ=l2-4mn>0时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个点P.方法总结:由于相似情况不明确,因此要分两种情况讨论,注意要找准对应边.三、板书设计相似三角形判定定理的证明判定定理1判定定理2判定定理3本课主要是证明相似三角形判定定理,以学生的自主探究为主,鼓励学生独立思考,多角度分析解决问题,总结常见的辅助线添加方法,使学生的推理能力和几何思维都获得提高,培养学生的探索精神和合作意识.

北师大初中数学九年级上册正方形的判定2教案
三:巩固新知1、判断对错:(1)如果一个菱形的两条对角线相等,那么它一定是正方形. ( )(2)如果一个矩形的两条对角线互相垂直,那么它一定是正方形.( )(3)两条对角线互相垂直平分且相等的四边形,一定是正方形. ( )(4)四条边相等,且有一个角是直角的四边形是正方形. ( )2、已知:点E、F、G、H分别是正方形ABCD四条边上的中点,并且E、F、G、H分别是AB、BC、CD、AD的中点.求证:四边形EFGH是正方形.3、自己完成课本P23的议一议四、小结1.正方形的判定方法.2.了解正方形、矩形、菱形之间的联系与区别,体验事物之间是相互联系但又有区别的辩证唯物主义观点.3.本节的收获与疑惑.

北师大初中数学九年级上册正方形的性质2教案
1)正方形的边长为4cm,则周长为( ),面积为( ) ,对角线长为( );2))正方形ABCD中,对角线AC、BD交于O点,AC=4 cm,则正方形的边长为( ), 周长为( ),面积为( )3)在正方形ABCD中,AB=12 cm,对角线AC、BD相交于O,OA= ,AC= 。4) 1、正方形具有而矩形不一定具有的性质是( ) A、四个角相等 B、对角线互相垂直平分 C、对角互补 D、对角线相等. 5)、正方形具有而菱形不一定具有的性质( ) A、四条边相等 B对角线互相垂直平分 C对角线平分一组对角 D对角线相等. 6)、正方形对角线长6,则它的面积为_________ ,周长为________. 7)、顺次连接正方形各边中点的小正方形的面积是原正方形面积的( )A.1/2 B.1/3 C.1/4 D.1/ 5四:范例讲解:1、(课本P21例1)学生自己阅读课本内容、注意证明过程的书写2、 如图,分别以△ABC的边AB,AC为一边向外画正方形AEDB和正方形ACFG,连接CE,BG.求证:BG=CE

北师大初中七年级数学上册从三个方向看物体的形状教案1
1.经历从不同方向观察物体的活动过程,发展空间观念.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的形状.3.能识别从三个方向看到的简单物体的形状,会画立方体及简单组合体从三个方向看到的形状,并能根据看到的形状描述基本几何体或实物原型.一、情境导入观察图中不同方向拍摄的庐山美景.你能从苏东坡《题西林壁》诗句:“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”体验出其中的意境吗?你能挖掘出其中蕴含的数学道理吗?让我们一起探索新知吧!二、合作探究探究点一:从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的,从上面看到的平面图形是()解析:这个几何体从上面看,共有2行,第一行能看到3个小正方形,第二行能看到2个小正方形.故选D.
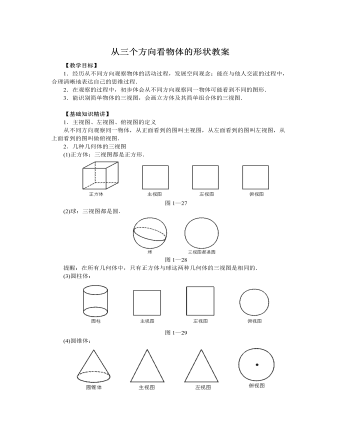
北师大初中七年级数学上册从三个方向看物体的形状教案2
【教学目标】1.经历从不同方向观察物体的活动过程,发展空间观念;能在与他人交流的过程中,合理清晰地表达自己的思维过程.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的图形.3.能识别简单物体的三视图,会画立方体及其简单组合体的三视图.【基础知识精讲】1.主视图、左视图、俯视图的定义从不同方向观察同一物体,从正面看到的图叫主视图,从左面看到的图叫左视图,从上面看到的图叫做俯视图.2.几种几何体的三视图(1)正方体:三视图都是正方形.圆锥的主视图、左视图都是三角形,而俯视图的图中有一个点表示圆锥的顶点,因为从上往下看圆锥时先看到圆锥的顶点,再看到底面的圆.3.如何画三视图 当用若干个小正方体搭成新的几何体,如何画这个新的几何体的三视图?

北师大初中七年级数学上册多边形和圆的初步认识教案1
方法总结:在分辨一个图形是否为多边形时,一定要抓住多边形定义中的关键词语,如“线段”“首尾顺次连接”“封闭”“平面图形”等.如此,对于某些似是而非的图形,只要根据定义进行对照和分析,即可判定.探究点二:确定多边形的对角线一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是()A.2015 B.2016 C.2017 D.2018解析:这个多边形的边数为2015+3=2018.故选D.方法总结:过n边形的一个顶点可以画出(n-3)条对角线.本题只要逆向求解即可.探究点三:求扇形圆心角将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,求这三个扇形圆心角的度数.解析:用扇形圆心角所对应的比去乘360°即可求出相应扇形圆心角的度数.解:三个扇形的圆心角度数分别为:360°×22+3+4=80°;360°×32+3+4=120°;

北师大初中七年级数学下册利用“角边角”“角角边”判定三角形全等教案
1.理解并掌握三角形全等的判定方法——“角边角”“角角边”;(重点)2.能运用“角边角”“角角边”判定方法解决有关问题.(难点) 一、情境导入如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪块去?学生活动:学生先自主探究出答案,然后再与同学进行交流.教师点拨:显然仅仅带①或②是无法配成完全一样的玻璃的,而仅仅带③则可以,为什么呢?本节课我们继续研究三角形全等的判定方法.二、合作探究探究点一:全等三角形判定定理“ASA”如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用“ASA”可得到△ADF≌△CBE.

北师大初中七年级数学下册三角形的内角和教案
解:∵CE⊥AF,∴∠DEF=90°,∴∠EDF=90°-∠F=90°-40°=50°.由三角形的内角和定理得∠C+∠DBC+∠CDB=∠F+∠DEF+∠EDF,又∵∠CDB=∠EDF,∴30°+∠DBC=40°+90°,∴∠DBC=100°.方法总结:本题主要利用了“直角三角形两锐角互余”的性质和三角形的内角和定理,熟记性质并准确识图是解题的关键.三、板书设计1.三角形的内角和定理:三角形的内角和等于180°.2.三角形内角和定理的证明3.直角三角形的性质:直角三角形两锐角互余.本节课通过一段对话设置疑问,巧设悬念,激发起学生获取知识的求知欲,充分调动学生学习的积极性,使学生由被动接受知识转为主动学习,从而提高学习效率.然后让学生自主探究,在教学过程中充分发挥学生的主动性,让学生提出猜想.在教学中,教师通过必要的提示指明学生思考问题的方向,在学生提出验证三角形内角和的不同方法时,教师注意让学生上台演示自己的操作过程和说明自己的想法,这样有助于学生接受三角形的内角和是180°这一结论

北师大初中七年级数学下册三角形的三边关系教案
方法总结:绝对值的化简首先要判断绝对值符号里面的式子的正负,然后根据绝对值的性质将绝对值的符号去掉,最后进行化简.此类问题就是根据三角形的三边关系,判断绝对值符号里面式子的正负,然后进行化简.三、板书设计1.三角形按边分类:有两边相等的三角形叫做等腰三角形,三边都相等的三角形是等边三角形,三边互不相等的三角形是不等边三角形.2.三角形中三边之间的关系:三角形任意两边之和大于第三边,三角形任意两边之差小于第三边.本节课让学生经历一个探究解决问题的过程,抓住“任意的三条线段能不能围成一个三角形”引发学生探究的欲望,围绕这个问题让学生自己动手操作,发现有的能围成,有的不能围成,由学生自己找出原因,为什么能?为什么不能?初步感知三条边之间的关系,重点研究“能围成三角形的三条边之间到底有什么关系”.通过观察、验证、再操作,最终发现三角形任意两边之和大于第三边这一结论.这样教学符合学生的认知特点,既增加了学习兴趣,又增强了学生的动手能力

北师大初中七年级数学下册用尺规作三角形教案
【类型三】 已知三边作三角形已知三条线段a、b、c,用尺规作出△ABC,使BC=a,AC=b、AB=c.解:作法:1.作线段BC=a;2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.三、板书设计1.已知两边及其夹角作三角形2.已知两角及其夹边作三角形3.已知三边作三角形本节课学习了有关三角形的作图,主要包括两种基本作图:作一条线段等于已知线段,作一个角等于已知角.作图时,鼓励学生一边作图,一边用几何语言叙述作法,培养学生的动手能力、语言表达能力

