-

北师大初中数学九年级上册相似三角形的周长和面积之比2教案
●教学目标(一)教学知识点1.相似三角形的周长比,面积比与相似比的关系.2. 相似三角形的周长比,面积比在实际中的应用.(二)能 力训练要求1.经历探索相似三角形的 性质的过程,培养学生的探索能力.2.利用相似三角形的性质解决实际问题训练学生的运用能力.(三)情 感与价值观要求1.学 生通过交流、归纳,总结相似三角形的周长比、面积比与相似比的关系,体会知识迁移、温故知新的好处.2.运用相似多边形的周长比,面积比解决实际问题,增强学生对知识的应用意识.●教学重点1.相似三角形的周长比、面积比与相似比关系的推导.2.运用相似三角形的比例关系解决实际问题.●教学难点相似三角形周长比、面积比与相似比的关系的推导及运用.●教学方法引导启发式通过温故知新,知识迁移,引导学生发现新的结论,通过比较、分析,应用获得的知识达到理解并掌握的 目的.●教具准备投影片两张第一张:(记作§4.7.2 A)第二张:(记作§4.7.2 B)

北师大初中九年级数学下册圆周角和圆心角的关系教案
解析:点E是BC︵的中点,根据圆周角定理的推论可得∠BAE=∠CBE,可证得△BDE∽△ABE,然后由相似三角形的对应边成比例得结论.证明:∵点E是BC︵的中点,即BE︵=CE︵,∴∠BAE=∠CBE.∵∠E=∠E(公共角),∴△BDE∽△ABE,∴BE∶AE=DE∶BE,∴BE2=AE·DE.方法总结:圆周角定理的推论是和角有关系的定理,所以在圆中,解决相似三角形的问题常常考虑此定理.三、板书设计圆周角和圆心角的关系1.圆周角的概念2.圆周角定理3.圆周角定理的推论本节课的重点是圆周角与圆心角的关系,难点是应用所学知识灵活解题.在本节课的教学中,学生对圆周角的概念和“同弧所对的圆周角相等”这一性质较容易掌握,理解起来问题也不大,而对圆周角与圆心角的关系理解起来则相对困难,因此在教学过程中要着重引导学生对这一知识的探索与理解.还有些学生在应用知识解决问题的过程中往往会忽略同弧的问题,在教学过程中要对此予以足够的强调,借助多媒体加以突出.

《夏日泛舟海上》教案
创设情景 学唱歌曲 1、导入:刚才老师给同学们看的是哪个季节的景色?我们都知道一年有四个季节,哪四个?你最喜欢哪个季节?为什么? 2、我们大家都知道威尼斯是著名的水上城市。今天老师就带同学们去看看世界著名的水上城市。看威尼斯水景的课件听歌曲《夏日泛舟海上》。 3、这部音乐作品什么地方最吸引你?(情绪、力度、速度、旋律、节奏等) 4、教师范唱歌曲,请同学们小声跟唱。 5、教师慢速弹旋律学生视谱练唱。 6、放录音学生跟唱歌曲, 让同学们思考用哪种声音演唱歌曲最为合适? 7、同学们用自然亲切的声音有感情的演唱歌曲。

《夏日里最后一朵玫瑰》教案
教学理念:本节课突出的是通过学习爱尔兰民歌,体会和认识爱尔兰的传统乐器——竖琴、风笛。并且通过竖笛训练,更好地体会歌曲的情感和内涵。引导学生认识东西方音乐的共通为之生死的永恒主题。教学目标:学会听辨其传统乐器——竖琴、风笛的音色,并且通过竖笛训练,引导学生认识东西方音乐的共通为之生死的永恒主题。教材分析:《夏日里最后一朵玫瑰》是一首古老的爱尔兰民歌。一八一三年托马斯·穆尔重新填词。贝多芬和门德尔松都曾根据它优美的旋律写过改编曲。 《夏日里最后一朵玫瑰》,词曲交融,倾注了作者们的无限深情。这首古老的西方民歌,引起了当代无数东方人的情感共鸣。必须承认,在东、西方民族的精神世界里,确有共通为之生死的永恒主题和文化价值观念。这首歌曲的结构特点是(A A B A )四个乐句。感受其切分音的节奏。X X.

《夏日泛舟海上》教案
教学目标 1.学唱歌曲《夏日泛舟海上》以及配乐散文朗诵《荷塘月色》。 2.通过不同的演唱形式,让学生感受欢快、活泼的风格特点,使学生了解音乐与文化作品在描绘夏日景象上异曲同工之妙笔,感受其审美意境。教学重点: 1.启发学生用自然、流畅、舒展的声音演唱《夏口泛舟海上》,并能准确的表达歌曲的情感。 2.掌握三拍子的特征及歌曲中音乐表情记号的作用。教学过程:第一环节:导入:1.播放歌曲《宁夏》;2.用语言导人。第二环节:学唱歌曲《夏日泛舟海上》1.接下来,老师要带同学们到美丽的大海上泛舟,请同学们在感受大自然美景的过程当中,也感受一下音乐的情绪。2.引导学生边听边感受歌曲的旋律、情绪有什么特点,播放录音范唱。3.请同学谈谈对歌曲的感受。

《夏日里最后一朵玫瑰》教案
教学目标:1、运用歌声和竖笛演奏,更深地体会这首世界名曲的委婉情绪,透过优美的旋律,感受人们对花开花谢,沧海桑田的人格化寄托,更好地体会歌曲的情感和内涵。2、通过学唱歌曲,采用聆听、体验、分析、师生互动的形式,更好地引导学生分析旋律的乐句和音乐情绪。设计意图:本课教学主要运用不同版本的音乐欣赏,让学生更好地体会世界人民对这首歌的喜爱。教学重点与难点:难点是吹准第三乐句的切分音节奏和变化音“#5”。教学过程:学习爱尔兰民歌《夏日里最后一朵玫瑰》师:今天我们一起来欣赏两个不同版本的歌曲,它们所表达的音乐情感有何异同?1、欣赏女声二重唱《夏日里最后一朵玫瑰》(怀念友人)2、欣赏德国电影《英俊少年》中的主题曲《夏日里最后一朵玫瑰》。(怀念母亲)3、导入主题:学习《夏日里最后一朵玫瑰》。学生用“LU”轻声哼唱旋律,并学唱歌曲和乐谱。4、分析乐句结构:(A A B A)分成四个乐句。典型的欧洲音乐风格特点。教师弹奏《故乡的亲人》进行对比分析音乐结构。

《夏日里最后一朵玫瑰》教案
教学理念:本课的音乐教学中主要围绕爱尔兰的民族音乐,有目的地选择最优秀的音乐音响作为教学研究的对象,采用“聆听”、“体验”、“分析”、“师生互动”的形式,运用歌声和竖笛演奏,更深地体会这首世界名曲的委婉情绪,透过优美的旋律,感受人们对花开花谢,沧海桑田的人格化寄托。教学过程:一、组织教学听音乐《伦敦德里小调》进课室。导入:这首音乐运用了什么乐器?你们知道哪个国家的国徽是一种乐器的图案?(师):简介爱尔兰的传统乐器(竖琴)。二、听《夏日里最后一朵玫瑰》。二、活动与练习:师生共同用歌声演绎这首《夏日里最后一朵玫瑰》。三、总结:今天我们通过学唱《夏日里最后一朵玫瑰》,让我们了解了哪个国家的音乐?(爱尔兰)它的传统乐器是什么?(竖琴)“花谢花开,沧海桑田。”我们的作曲家能够捕捉这个共通为之生死的主题,创作出朗朗上口的旋律,给予我们莫大的精神熏陶。

《夏日泛舟海上》教案
教学过程 :1、直接导入:今天我给同学们带来了一首歌曲,你们听一听,歌曲表现的是哪个季节?歌词唱出了什么内容?(1)播放音乐(学生听音乐,思考问题)(2)歌词唱出了什么内容?(学生稍作讨论回答问题)(3)你还能不能用语言来概括一下夏天是什么样子的?(学生讨论)2、为了使同学们更深刻的感受夏日情怀,老师将带领同学们乘上小舟,去享受夏日泛舟的乐趣。在出发之前,我们先来学一首歌曲。大家看大屏幕听歌曲,注意听这首歌曲是几拍子的?能不能听出它的强弱关系来?(1)播放《夏日泛舟海上》。(2)找学生回答歌曲是几拍子的、强弱规律。(3)歌曲的情绪是怎样的?(4)复听一遍歌曲,考虑一下八三拍的这种强弱规律表现了歌曲的什么意境?3、那么同学们想不想用一种喜悦的心情来唱一唱呢?(1)第三遍播放歌曲,学生跟唱。(2)在演唱时出现的难点处理:结束句、三连音的处理。(3)共同处理难点。(4)带上歌词唱一唱更准确的掌握节奏。(5)下面跟老师来唱一唱。你想用什么样的声音唱呢?(6)你们发现了吗?歌曲里还有很多特殊的记号呢,他们可是为歌曲的情绪起了很大的作用啊。你们能说一说都有哪些记号?作用是什么?(7)把各种力度记号融合在歌曲里用乐观、充满活力的情绪唱一唱歌曲。(8)变换演唱形式。(分组等)4、大家想一想当我们学唱了歌曲《夏日泛舟海上》后,还可以通过什么形式和方法,抒发我们对明媚的夏季情怀呢?

大班美术教案夏夜
2、尝试用喷刷做画的游戏方法绘出美丽的夜色,感受色彩的变化美,培养幼儿初步的审美能力。准 备: 1、做画工具牙刷,废塑料筐残片剪成的喷刷用具每人一个,三色水粉(蓝、绿、青)、剪纸若干份,颜色卡幼儿人手一份,教师示范用纸、录音机、磁带各一。 2、课前让幼儿认识剪影并观察美丽的夏夜。过 程: 1、引出课题:放音乐《夏夜》将幼儿带到夜暮降临、万物寂静的特定环境中,提问: ①请小朋友听一段音乐,你在音乐中听到了什么?这段音乐表现的是什么时候?(如小蟋蟀叫、月亮、星星出来了等、晚上)

小班主题:夏天课件教案
二、 活动目标:1、 通过活动使幼儿感知夏天的特征,能够区分夏天与春天的不同之处。2、 知道夏天热了,要多喝水、勤洗澡,注意个人卫生。3、 能够知道几种避暑的方法。三、 活动与指导:学习活动方案(一)内 容认识夏天活动目标1、通过观察夏天的景色和各种树叶、小草的变化,初步知道夏天到了。2了解夏天的特征,萌发幼儿对大自然的热爱之情。活动准备活动前让父母带幼儿去公园帮助观察夏天的景色和各种树叶、小草的变化,散步活动时引导幼儿观赏幼儿园的风景。流 程谈话活动----欣赏图片----布置墙面

北师大初中七年级数学上册生活中的立体图形教案1
解析:此题作为一道开放型题,分类的方法非常多,只要能说明分类的理由即可.但要注意:按某一标准分类时,要做到不重不漏,分类标准不同时,分类的结果也就不尽相同.解:本题答案不唯一,如按柱体、锥体、球体分类:(2)(3)(5)和(6)都是柱体,(4)(7)是锥体,(1)是球体.方法总结:生活中常见几何体有两种分类:一种按柱体、锥体、球体分类;一种按平面和曲面分类.探究点二:几何体的形成笔尖画线可以理解为点动成线.使用数学知识解释下列生活中的现象:(1)流星划破夜空,留下美丽的弧线;(2)一条拉直的细线切开了一块豆腐;(3)把一枚硬币立在桌面上用力一转,形成一个球.解析:解释现象关键是看其属于什么运动.解:(1)点动成线;(2)线动成面;(3)面动成体.方法总结:生活中的很多现象都可以用数学知识来解释,关键是要找到生活实例与数学知识的连接点,如第(1)题可将流星看作一个点,则“点动成线”.如图所示,将平面图形绕轴旋转一周,得到的几何体是()
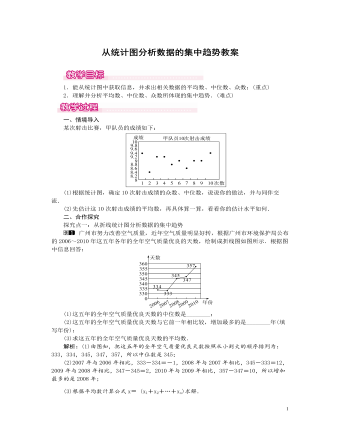
北师大初中数学八年级上册从统计图分析数据的集中趋势1教案
1.能从统计图中获取信息,并求出相关数据的平均数、中位数、众数;(重点)2.理解并分析平均数、中位数、众数所体现的集中趋势.(难点)一、情境导入某次射击比赛,甲队员的成绩如下:(1)根据统计图,确定10次射击成绩的众数、中位数,说说你的做法,并与同伴交流.(2)先估计这10次射击成绩的平均数,再具体算一算,看看你的估计水平如何.二、合作探究探究点一:从折线统计图分析数据的集中趋势广州市努力改善空气质量,近年空气质量明显好转,根据广州市环境保护局公布的2006~2010年这五年各年的全年空气质量优良的天数,绘制成折线图如图所示.根据图中信息回答:(1)这五年的全年空气质量优良天数的中位数是________;(2)这五年的全年空气质量优良天数与它前一年相比较,增加最多的是________年(填写年份);(3)求这五年的全年空气质量优良天数的平均数.解析:(1)由图知,把这五年的全年空气质量优良天数按照从小到大的顺序排列为:333,334,345,347,357,所以中位数是345;

北师大初中数学九年级上册投影的概念与中心投影1教案
∴∠AEP=∠ACB,∠APE=∠ABC,∴△AEP∽△ACB.∴PECB=APAB,即1.89=2AB,解得AB=10(m).∴QB=AB-AP-PQ=10-2-6.5=1.5(m),即小明站在点Q时在路灯AD下影子的长度为1.5m;(2)同理可证△HQB∽△DAB,∴HQDA=QBAB,即1.8AD=1.510,解得AD=12(m).即路灯AD的高度为12m.方法总结:解决本题的关键是构造相似三角形,然后利用相似三角形的性质求出对应线段的长度.三、板书设计投影的概念与中心投影投影的概念:物体在光线的照射下,会 在地面或其他平面上留 下它的影子,这就是投影 现象中心投影概念:点光源的光线形成的 投影变化规律影子是生活中常见的现象,在探索物体与其投影关系的活动中,体会立体图形与平面图形的相互转化关系,发展学生的空间观念.通过在灯光下摆弄小棒、纸片,体会、观察影子大小和形状的变化情况,总结规律,培养学生观察问题、分析问题的能力.

北师大初中九年级数学下册三角函数的计算1教案
如图,课外数学小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直.他们在A处测得塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,小山坡坡顶E的仰角∠EBN=25.6°.现在请你帮助课外活动小组算一算塔高DE大约是多少米(结果精确到个位).解析:根据锐角三角函数关系表示出BF的长,进而求出EF的长,得出答案.解:延长DE交AB延长线于点F,则∠DFA=90°.∵∠A=45°,∴AF=DF.设EF=x,∵tan25.6°=EFBF≈0.5,∴BF=2x,则DF=AF=50+2x,故tan61.4°=DFBF=50+2x2x=1.8,解得x≈31.故DE=DF-EF=50+31×2-31=81(米).所以,塔高DE大约是81米.方法总结:解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形.

北师大初中数学九年级上册正方形的性质1教案
在Rt△ABC中,AC=AB2+BC2=12+12=2(cm),∴FC=AC-AF=2-1(cm),∴BE=2-1(cm).方法总结:正方形被对角线分成4个等腰直角三角形,因此在正方形中解决问题时常用到等腰三角形的性质与直角三角形的性质.【类型三】 利用正方形的性质证明线段相等如图,已知过正方形ABCD的对角线BD上一点P,作PE⊥BC于点E,PF⊥CD于点F,求证:AP=EF.解析:由PE⊥BC,PF⊥CD知四边形PECF为矩形,故有EF=PC,这时只需说明AP=CP,由正方形对角线互相垂直平分可知AP=CP.证明:连接AC,PC,如图.∵四边形ABCD为正方形,∴BD垂直平分AC,∴AP=CP.∵PE⊥BC,PF⊥CD,∠BCD=90°,∴四边形PECF为矩形,∴PC=EF,∴AP=EF.方法总结:(1)在正方形中,常利用对角线互相垂直平分证明线段相等;(2)无论是正方形还是矩形,经常连接对角线,这样可以使分散的条件集中.

北师大初中七年级数学上册比较线段的长短教案1
1.了解“两点之间,线段最短”.2.能借助尺、规等工具比较两条线段的大小,能用圆规作一条线段等于已知线段.3.了解线段的中点及线段的和、差、倍、分的意义,并能根据条件求出线段的长.一、情境导入爱护花草树木是我们每个人都应具备的优秀品质.从教学楼到图书馆,总有少数同学不走人行道而横穿草坪(如图),同学们,你觉得这样做对吗?为了解释这种现象,学习了下面的知识,你就会知道.二、合作探究探究点一:线段长度的计算【类型一】 根据线段的中点求线段的长如图,若线段AB=20cm,点C是线段AB上一点,M、N分别是线段AC、BC的中点.(1)求线段MN的长;(2)根据(1)中的计算过程和结果,设AB=a,其它条件不变,你能猜出MN的长度吗?请用简洁的话表达你发现的规律.

北师大初中七年级数学上册从三个方向看物体的形状教案1
1.经历从不同方向观察物体的活动过程,发展空间观念.2.在观察的过程中,初步体会从不同方向观察同一物体可能看到不同的形状.3.能识别从三个方向看到的简单物体的形状,会画立方体及简单组合体从三个方向看到的形状,并能根据看到的形状描述基本几何体或实物原型.一、情境导入观察图中不同方向拍摄的庐山美景.你能从苏东坡《题西林壁》诗句:“横看成岭侧成峰,远近高低各不同.不识庐山真面目,只缘身在此山中.”体验出其中的意境吗?你能挖掘出其中蕴含的数学道理吗?让我们一起探索新知吧!二、合作探究探究点一:从不同的方向看物体如图所示的几何体是由一些小正方体组合而成的,从上面看到的平面图形是()解析:这个几何体从上面看,共有2行,第一行能看到3个小正方形,第二行能看到2个小正方形.故选D.

北师大初中七年级数学上册代数式的求值教案1
(1)请你用代数式表示水渠的横断面面积;(2)计算当a=3,b=1时,水渠的横断面面积.解析:(1)根据梯形面积=12(上底+下底)×高,即可用含有a、b的代数式表示水渠横断面面积;(2)把a=3、b=1带入到(1)中求出的代数式中,其结果即为水渠的横断面面积.解:(1)∵梯形面积=12(上底+下底)×高,∴水渠的横断面面积为:12(a+b)b(m2);(2)当a=3,b=1时水渠的横断面面积为12(3+1)×1=2(m2).方法总结:解答本题时需搞清下列几个问题:(1)题目中给出的是什么图形?(2)这种图形的面积公式是什么?(3)根据公式求图形的面积需要知道哪几个量?(4)这些量是否已知或能求出?搞清楚了这些问题,求解就水到渠成.三、板书设计教学过程中,应通过活动使学生感知代数式运算在判断和推理上的意义,增强学生学习数学的兴趣,培养学生积极的情感和态度,为进一步学习奠定坚实的基础.

北师大初中七年级数学上册等式的基本性质教案1
方法总结:对等式进行变形,必须在等式的两边同时进行,即同加或同减,同乘或同除,不能漏掉一边,且同加或同减,同乘或同除的数必须相同.探究点二:利用等式的基本性质解方程用等式的性质解下列方程:(1)4x+7=3; (2)12x-13x=4.解析:(1)在等式的两边都减7,再在等式的两边都除以4,可得答案;(2)在等式的两边都乘以6,再合并同类项,可得答案.解:(1)方程两边都减7,得4x=-4.方程两边都除以4,得x=-1;(2)方程两边都乘以6,得3x-2x=24,x=24.方法总结:解方程时,一般先将方程变形为ax=b的形式,然后再变形为x=c的形式.三、板书设计教学过程中,强调学生自主探索和合作交流,通过观察、操作、归纳等数学活动,感受数学思想的条理性和数学结论的严密性.

北师大初中七年级数学上册多边形和圆的初步认识教案1
方法总结:在分辨一个图形是否为多边形时,一定要抓住多边形定义中的关键词语,如“线段”“首尾顺次连接”“封闭”“平面图形”等.如此,对于某些似是而非的图形,只要根据定义进行对照和分析,即可判定.探究点二:确定多边形的对角线一个多边形从一个顶点最多能引出2015条对角线,这个多边形的边数是()A.2015 B.2016 C.2017 D.2018解析:这个多边形的边数为2015+3=2018.故选D.方法总结:过n边形的一个顶点可以画出(n-3)条对角线.本题只要逆向求解即可.探究点三:求扇形圆心角将一个圆分割成三个扇形,它们的圆心角的度数之比为2:3:4,求这三个扇形圆心角的度数.解析:用扇形圆心角所对应的比去乘360°即可求出相应扇形圆心角的度数.解:三个扇形的圆心角度数分别为:360°×22+3+4=80°;360°×32+3+4=120°;

