-
人教版高中政治必修3坚持先进文化的前进方向精品教案
一、教材分析这一课对学生来说还是有点难度的，比较抽象，和同学们的生活离得比较远。这一课也是第四单元的点睛一课，重点。可以列举当前我国社会主义精神文明建设的事例，说明必须坚持马克思主义的指导地位，用“三个代表”重要思想统领社会主义文化建设；理解发展先进文化，就是发展面向现代化、面向世界、面向未来的，民族的科学的大众的社会主义文化。例如，“五个一工程”等奖项；“希望工程”等活动。让学生来理解我国社会主义文化的发展。二、教学目标（一）知识目标（1）当代中国先进文化的科学内涵及文化建设的指导思想理解：（2）社会主义核心价值体系的地位、内容及要求，（3）坚持马克思主义指导地位的必要性和重要性（4）引领中国先进文化前进方向的永不退色的旗帜分析：运用相关知识，，说明必须用“三个代表”重要思想统领社会主义文化建设
人教版高中历史必修1夏、商、西周的政治制度教案3篇
【大宗与小宗的关系：君臣关系、兄弟关系】4、影响：宗法制保证了贵族在政治上的垄断和特权地位，也有利于统治集团内部的稳定和团结。【合作探究】分封制与宗法制的关系两者互为表里、相辅相成：从根本上说，分封制就是宗法制作用于国家地方政治制度的重要举措和体现。宗法制是分封制的内核和纽带，维护贵族统治集团内部的稳定与团结。宗法制与分封制结合紧密，宗法制是西周政治制度的基础，分封制基于宗法制而产生，与宗法制互为表里。小结：我国早期政治制度（夏商周）发展脉络：起源于夏——初步建立于夏商——完善于西周——瓦解于西周末年到春秋——崩溃于战国★问题解答⊙【学思之窗】从这段记载，你能看出商朝的相权有多大吗？答案提示：相是商朝中央最高官吏，相权很大，包括参定政制、主持政务、辅佐商王等，甚至有时可废立商王。
人教版高中历史必修3建国以来的重大科技成就教案
思考：1）材料1、2反映了一个什么样的严重问题？（饥饿和粮食问题）2）材料3中，中国农民为什么那样说？（邓小平在全国实行的以家庭联产承包责任制为主要形式的责任制调动了农民生产的积极性，解放了农村生产力，推动了农业的发展；袁隆平的杂交水稻提高了水稻产量，增加了农民的收入，解决了农民的吃饭问题）3）据以上材料指出，袁隆平研究的交水稻有何重大意义？（杂交稻不仅解决了中国人的吃饭问题；而且其在世界范围的推广，也有助于解决世界性的饥饿问题）四、计算机技术与生物技术的发展1、20世纪50年代，我国开始了计算机的研制工作；2、1983年，我国成功研制出巨型计算机“银河-Ⅰ号”，加速了国家信息化的发展；3、1965年，中国首次人工合成结晶牛胰岛素(在世界上第一次用人工方法合成出具有生物活性的蛋白质——结晶牛胰岛素) 。4、积极参与人类基因的研究(唯一的发展中国家)。
人教版高中政治必修3传统文化的继承精品教案
一、教材分析在文化传承的过程中，如果说文化传播是文化横向积累过程，那么文化继承就是文化纵向积累的过程，第四课围绕文化继承与文化发展的关系，继续讲述文化传承的过程。本框内容主要解析中华传统文化在现实生活中的作用，阐述继承传统文化，发挥传统文化的积极作用的正确态度是“取其精华，去其糟粕”。一、 教学目标1、知识目标通过介绍传统习俗、传统建筑、传统文艺、传统思想在现代社会生活各方面的延续及其影响，让学生了解文化的继承性。分析传统文化的相对稳定性和鲜明的民族性，解析中华民族传统文化在现实生活中的作用，知道符合社会发展规律的传统文化对社会与人的发展的积极作用，而一成不变的传统文化则会起阻碍社会进步、妨害发展的消极作用。明确一个民族、一个国家只有发挥传统文化的积极作用，克服传统文化的消极作用，才能兴旺发达的道理；阐述继承传统文化，发挥传统文化的积极作用的正确态度是“取其精华，去其糟粕”。
人教版高中政治必修4用对立统一的观点看问题精品教案
1、重点：如何处理主次矛盾、矛盾主次方面的关系，具体问题具体分析2、难点：弄清主次矛盾、矛盾主次方面的含义四、学情分析高二学生具备了一定的抽象思维和综合分析的能力,但实践能力普遍较弱。本框所学知识理论性较强，主次矛盾和矛盾的主次方面这两个概念极易混淆，学生较难理解。而且本框内容属方法论要求，需要学生将理论与实践紧密结合，学生在运用理论分析实际问题上还比较薄弱。五、教学方法：1、探究性学习法。组织学生课后分小组进行探究性学习。在探究性学习中进行：“自主学习”、“合作学习”。让学生进行自主学习的目的是：让学生作学习的主人，“爱学、乐学”，并培养学生终身学习的能力；让学生进行合作学习的目的是：在小组分工合作中，在生生互动（ 学生与学生互动）中，促使学生克服“以自我为中心，合作精神差，实践能力弱“等不足，培养综合素质。2、理论联系实际法。关注生活，理论联系实际,学以致用。
人教版高中政治必修2民主选举：投出理性的一票教案
教师活动：那种“选举与我无关”，“选谁都可以”的想法，是公民意识不强、主人翁意识不强的表现。那么，怎样才能行使好自己的选举权呢？请同学们根据上面的学习，谈谈自己的想法。学生活动：思考讨论教师点评：2、 如何行使好自己的选举权（1）要不断提高自己参与民主选举的素养，端正参加选举的态度，提高选举能力，选出切实能代表人民利益的人。（2）要增强主人翁责任感和公民参与意识，积极参加选举，认真行使自己的选举权。（3）要不断提高政治参与能力，在理性判断基础上，郑重投出自己的一票。（三）课堂总结、点评本节内容讲述了我国的选举方式以及如何珍惜自己的选举权利的有关知识，懂得我国是人民民主专政的社会主义国家，人民当家作主，应该增强主人翁责任感，自觉珍惜并运用好选举权，以促进我国的民主政治建设，维护人民的根本利益。
人教版高中政治必修2处理民族关系的原则-平等、团结、共同繁荣说课稿
环节四 情感升华，感悟生活播放《爱我中华》，感受祖国的伟大，民族的团结。设计意图：使学生感受伟大的中华民族的精神，内心产生共鸣，抒发强烈的爱国热情。教师带领学生一起合唱，用歌声结束本堂课内容，能再次唤起学生的爱国情感，使学生认识到：维护国家统一和民族团结是每个公民的义务。环节五 课堂小结 巩固知识本节课我采用线索性的板书，整个知识结构一目了然，为了充分发挥学生在课堂的主体地位，我将课堂小结交由学生完成，请学生根据课堂学习的内容，结合我的板书设计来进行小结，以此来帮助教师在第一时间掌握学生学习信息的反馈，同时培养学生归纳分析能力、概括能力。本节课，我根据建构主义理论，强调学生是学习的中心，学生是知识意义的主动建构者，是信息加工的主体，要强调学生在课堂中的参与性、以及探究性，不仅让他们懂得知识，更让他们相信知识，并且将知识融入到实践当中去，最终达到知、情、意、行的统一。
人教版高中政治必修2国际社会的主要成员-主权国家和国际组织说课稿
【教师总结：联合国的会徽的世界地图象征着联合国是一个世界性的国际组织；图案中得橄榄枝象征着和平。联合国采取了很多措施以实现它的宗旨，如对于朝鲜违反国际法规进行核试验，联合国给予警告和制裁，充分体现了它维护国际和平与安全，促进国际合作与发展的宗旨。】对于中国与联合国的关系这部分内容，我将请阅读教材92页几幅图片及材料内容，设置活动探究课中国在联合国的声音和身影，请合作讨论思考以下两个问题，中国与联合国的关系；列举事实说明中国在国际社会中的重要作用。 教师通过剖析中国在联合国的地位和作用，引导学生理解中国在国际社会中发挥着重要作用，是负责任的国家；同时培养学生综合运用知识分析说明问题的能力，使学生感受作为中国人的自豪。【教师总结：中国是联合国的创始国之一，中国作为联合国的创始国和安理会常任理事国之一，一贯遵循联合国宪章的宗旨和原则，积极参与联合国及其专门机构有利于世界和平和发展的活动。】
XX年上期第三周国旗下讲话稿：不做熊孩子
老师们，同学们，大家早上好。这是一个由乐高积木拼成的尼克狐的头部。这是完成的下半身。现在，中间的身子和下半身拼在了一起，就等安上头部就ok了。哇呀！终于完成了。一个高将近1.8米的尼克狐，由上万块乐高积木组成，价值10万多元。年轻的作者陈叔叔为了制作它，三天三夜不眠不休。但是，这件作品展出了1个小时后，有个4、5岁的小男孩钻进隔离区域，在合影的过程中，他推了一下尼克。尼克狐瞬间碎成了一堆渣子。有个正在8楼屋内看动画片《喜羊羊》的10岁男孩，因嫌楼外施工的电钻声太吵，一气之下，用小刀子将施工者下方的安全绳割断，致使其悬在半空动弹不得，经消防大队紧急出动后才将人安全救下。去年4月，有一个成都的女子在机场出境时被拦，原来是自家孩子在港澳通行证上涂鸦，不能使用了。
人教A版高中数学必修一对数的运算教学设计（1）
本节课是新版教材人教A版普通高中课程标准实验教科书数学必修1第四章第4.3.2节《对数的运算》。其核心是弄清楚对数的定义，掌握对数的运算性质，理解它的关键就是通过实例使学生认识对数式与指数式的关系，分析得出对数的概念及对数式与指数式的 互化，通过实例推导对数的运算性质。由于它还与后续很多内容，比如对数函数及其性质,这也是高考必考内容之一，所以在本学科有着很重要的地位。解决重点的关键是抓住对数的概念、并让学生掌握对数式与指数式的互化；通过实例推导对数的运算性质，让学生准确地运用对数运算性质进行运算，学会运用换底公式。培养学生数学运算、数学抽象、逻辑推理和数学建模的核心素养。1、理解对数的概念，能进行指数式与对数式的互化；2、了解常用对数与自然对数的意义，理解对数恒等式并能运用于有关对数计算。
人教A版高中数学必修一对数的概念教学设计（2）
对数与指数是相通的，本节在已经学习指数的基础上通过实例总结归纳对数的概念，通过对数的性质和恒等式解决一些与对数有关的问题.课程目标1、理解对数的概念以及对数的基本性质；2、掌握对数式与指数式的相互转化；数学学科素养1.数学抽象：对数的概念；2.逻辑推理：推导对数性质；3.数学运算：用对数的基本性质与对数恒等式求值；4.数学建模：通过与指数式的比较，引出对数定义与性质.重点：对数式与指数式的互化以及对数性质；难点：推导对数性质．教学方法：以学生为主体，采用诱思探究式教学，精讲多练。教学工具：多媒体。一、 情景导入已知中国的人口数y和年头x满足关系 中，若知年头数则能算出相应的人口总数。反之，如果问“哪一年的人口数可达到18亿，20亿，30亿......”，该如何解决？要求：让学生自由发言，教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修一函数的概念教学设计（2）
函数在高中数学中占有很重要的比重，因而作为函数的第一节内容，主要从三个实例出发，引出函数的概念.从而就函数概念的分析判断函数，求定义域和函数值，再结合三要素判断函数相等.课程目标1.理解函数的定义、函数的定义域、值域及对应法则。2.掌握判定函数和函数相等的方法。3.学会求函数的定义域与函数值。数学学科素养1.数学抽象：通过教材中四个实例总结函数定义；2.逻辑推理：相等函数的判断；3.数学运算：求函数定义域和求函数值；4.数据分析：运用分离常数法和换元法求值域；5.数学建模：通过从实际问题中抽象概括出函数概念的活动，培养学生从“特殊到一般”的分析问题的能力，提高学生的抽象概括能力。重点：函数的概念，函数的三要素。难点：函数概念及符号y=f(x)的理解。
人教A版高中数学必修一对数的运算教学设计（2）
学生已经学习了指数运算性质，有了这些知识作储备，教科书通过利用指数运算性质，推导对数的运算性质，再学习利用对数的运算性质化简求值。课程目标1、通过具体实例引入，推导对数的运算性质；2、熟练掌握对数的运算性质，学会化简，计算.数学学科素养1.数学抽象：对数的运算性质；2.逻辑推理：换底公式的推导；3.数学运算：对数运算性质的应用；4.数学建模：在熟悉的实际情景中，模仿学过的数学建模过程解决问题.重点：对数的运算性质，换底公式，对数恒等式及其应用；难点：正确使用对数的运算性质和换底公式．教学方法：以学生为主体，采用诱思探究式教学，精讲多练。教学工具：多媒体。一、 情景导入回顾指数性质：(1)aras＝ar＋s(a＞0，r，s∈Q)．(2)(ar)s＝ (a＞0，r，s∈Q)．(3)(ab)r＝ (a＞0，b＞0，r∈Q)．那么对数有哪些性质？如 要求：让学生自由发言，教师不做判断。而是引导学生进一步观察.研探.
人教A版高中数学必修一集合的概念教学设计（2）
例7 用描述法表示抛物线y＝x2＋1上的点构成的集合．【答案】见解析 【解析】 抛物线y＝x2＋1上的点构成的集合可表示为：{(x，y)|y＝x2＋1}．变式1．[变条件，变设问]本题中点的集合若改为“{x|y＝x2＋1}”，则集合中的元素是什么？【答案】见解析 【解析】集合{x|y＝x2＋1}的代表元素是x，且x∈R，所以{x|y＝x2＋1}中的元素是全体实数．变式2．[变条件，变设问]本题中点的集合若改为“{y|y＝x2＋1}”，则集合中的元素是什么？【答案】见解析 【解析】集合{ y| y＝x2＋1}的代表元素是y，满足条件y＝x2＋1的y的取值范围是y≥1，所以{ y| y＝x2＋1}＝{ y| y≥1}，所以集合中的元素是大于等于1的全体实数．解题技巧（认识集合含义的2个步骤）一看代表元素，是数集还是点集，二看元素满足什么条件即有什么公共特性。
高中物理必修1教案高中物理必修二圆周运动教案
一、描述圆周运动的物理量 探究交流 打篮球的同学可能玩过转篮球，让篮球在指尖旋转，展示自己的球技，如图5-4-1所示.若篮球正绕指尖所在的竖直轴旋转，那么篮球上不同高度的各点的角速度相同吗?线速度相同吗? 【提示】 篮球上各点的角速度是相同的.但由于不同高度的各点转动时的圆心、半径不同，由v=ωr可知不同高度的各点的线速度不同.
高中物理必修二圆周运动教案
1、知识与技能 (1)认识匀速圆周运动的概念，理解线速度的概念，知道它就是物体做匀速圆周运动的瞬时速度;理解角速度和周期的概念，会用它们的公式进行计算; (2)理解线速度、角速度、周期之间的关系：v=rω=2πr/T; (3)理解匀速圆周运动是变速运动。 2、过程与方法 (1)运用极限法理解线速度的瞬时性.掌握运用圆周运动的特点如何去分析有关问题; (2)体会有了线速度后.为什么还要引入角速度.运用数学知识推导角速度的单位。
必修一牛顿第一定律教案
(二)?过程与方法? 4.?观察生活中的惯性现象，了解力和运动的关系? 5.?通过实验加深对牛顿第一定律的理解? 6.?理解理想实验是科学研究的重要方法? (三)?情感态度与价值观? 7.?通过伽利略和亚里士多德对力和运动关系的不同认识，了解人类认识事物本质的曲折性? 8.?感悟科学是人类进步的不竭动力
人教版新课标高中物理必修1匀变速直线运动的速度与时间的关系教案2篇
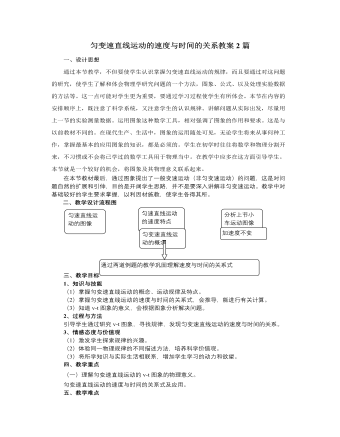
一、设计思想通过本节教学，不但要使学生认识掌握匀变速直线运动的规律，而且要通过对这问题的研究，使学生了解和体会物理学研究问题的一个方法，图象、公式、以及处理实验数据的方法等。这一点可能对学生更为重要，要通过学习过程使学生有所体会。本节在内容的安排顺序上，既注意了科学系统，又注意学生的认识规律。讲解问题从实际出发，尽量用上一节的实验测量数据。运用图象这种数学工具，相对强调了图象的作用和要求。这是与以前教材不同的。在现代生产、生活中，图象的运用随处可见，无论学生将来从事何种工作，掌握最基本的应用图象的知识，都是必须的。学生在初学时往往将数学和物理分割开来，不习惯或不会将已学过的数学工具用于物理当中。在教学中应多在这方面引导学生。本节就是一个较好的机会，将图象及其物理意义联系起来。
人教版新课标高中物理必修1匀变速直线运动的位移与时间的关系教案2篇
一、教学目标1．知识与技能：(1)知道匀速直线运动的位移x＝υt对应着 图象中的矩形面积．(2)掌握匀变速直线运动的位移与时间关系的公式 ,及其简单应用．(3)掌握匀变速直线运动的位移与速度关系的公式 ,及其简单应用．2．过程与方法：(1)让学生初步了解探究学习的方法．(2)培养学生运用数学知识-----函数图象的能力．(3)培养学生运用已知结论正确类比推理的能力．3．情感态度与价值观：(1)培养学生认真严谨的科学分析问题的品质．(2)从知识是相互关联、相互补充的思想中，培养学生建立事物是相互联系的唯物主义观点．(3)培养学生应用物理知识解决实际问题的能力．二、教学重点、难点1．教学重点及其教学策略：重点：(1)匀变速直线运动的位移与时间关系的公式 及其应用．(2)匀变速直线运动的位移与速度关系的公式 及其应用．教学策略：通过思考讨论和实例分析来加深理解．
人教版新课标高中物理必修1匀变速直线运动的速度与时间的关系教案2篇
一、设计思想通过本节教学，不但要使学生认识掌握匀变速直线运动的规律，而且要通过对这问题的研究，使学生了解和体会物理学研究问题的一个方法，图象、公式、以及处理实验数据的方法等。这一点可能对学生更为重要，要通过学习过程使学生有所体会。本节在内容的安排顺序上，既注意了科学系统，又注意学生的认识规律。讲解问题从实际出发，尽量用上一节的实验测量数据。运用图象这种数学工具，相对强调了图象的作用和要求。这是与以前教材不同的。在现代生产、生活中，图象的运用随处可见，无论学生将来从事何种工作，掌握最基本的应用图象的知识，都是必须的。学生在初学时往往将数学和物理分割开来，不习惯或不会将已学过的数学工具用于物理当中。在教学中应多在这方面引导学生。本节就是一个较好的机会，将图象及其物理意义联系起来。