-

北师大初中七年级数学下册多项式除以单项式教案
一、情境导入1.计算:(1)-6x3y4z2÷(-23x2y2);(2)9mn÷(-6mn)2·(13n2);(3)6(a-b)3c5÷[-35(a-b)2c]·[-2(a-b)3c4].2.m(a+b+c)=am+bm+cm,(am+bm+cm)÷m=am÷m+bm÷m+cm÷m=a+b+c.你能根据多项式乘以单项式的运算归纳出多项式除以单项式的运算法则吗?二、合作探究探究点:多项式除以单项式【类型一】 直接利用多项式除以单项式进行计算计算:(72x3y4-36x2y3+9xy2)÷(-9xy2).解析:根据多项式除以单项式,先用多项式的每一项分别除以这个单项式,然后再把所得的商相加.解:原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)+9xy2÷(-9xy2)=-8x2y2+4xy-1.方法总结:多项式除以单项式,先把多项式的每一项都分别除以这个单项式,然后再把所得的商相加.

北师大初中七年级数学下册利用“边边边”判定三角形全等教案
解析:由于多边形(三边以上的)不具有稳定性,将其转化为三角形后木架的形状就不变了.根据具体多边形转化为三角形的经验及题中所加木条可找到一般规律.解:过n边形的一个顶点可以作(n-3)条对角线,把多边形分成(n-2)个三角形,所以,要使一个n边形木架不变形,至少需要(n-3)根木条固定.方法总结:将多边形转化为三角形时,所需要的木条根数,可从具体到一般去发现规律,然后验证求解.三、板书设计1.边边边:三边对应相等的两个三角形全等,简写成“边边边”或“SSS”.2.三角形的稳定性本节课从操作探究活动入手,有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边边边”掌握较好,达到了教学的预期目的.存在的问题是少数学生在辅助线的构造上感到困难,不知道如何添加合理的辅助线,还需要在今后的教学中进一步加强巩固和训练

北师大初中七年级数学下册利用“边角边”判定三角形全等教案
AD=CD,∠ADE=∠CDG,DE=GD,∴△ADE≌△CDG(SAS),∴AE=CG;(2)设AE与DG相交于M,AE与CG相交于N.在△GMN和△DME中,由(1)得∠CGD=∠AED,又∵∠GMN=∠DME,∠DEM+∠DME=90°,∴∠CGD+∠GMN=90°,∴∠GNM=90°,∴AE⊥CG.三、板书设计1.边角边:两边及其夹角分别相等的两个三角形全等,简写成“边角边”或“SAS”.两边和其中一边的对角对应相等的两个三角形不一定全等.2.全等三角形判定与性质的综合运用本节课从操作探究入手,具有较强的操作性和直观性,有利于学生从直观上积累感性认识,从而有效地激发了学生的学习积极性和探究热情,提高了课堂的教学效率,促进了学生对新知识的理解和掌握.从课堂教学的情况来看,学生对“边角边”掌握较好,但在探究三角形的大小、形状时不会正确分类,需要在今后的教学和作业中进一步加强分类思想的巩固和训练

北师大初中七年级数学下册利用“角边角”“角角边”判定三角形全等教案
1.理解并掌握三角形全等的判定方法——“角边角”“角角边”;(重点)2.能运用“角边角”“角角边”判定方法解决有关问题.(难点) 一、情境导入如图所示,某同学把一块三角形的玻璃不小心打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带哪块去?学生活动:学生先自主探究出答案,然后再与同学进行交流.教师点拨:显然仅仅带①或②是无法配成完全一样的玻璃的,而仅仅带③则可以,为什么呢?本节课我们继续研究三角形全等的判定方法.二、合作探究探究点一:全等三角形判定定理“ASA”如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用“ASA”可得到△ADF≌△CBE.

北师大初中七年级数学下册用尺规作三角形教案
【类型三】 已知三边作三角形已知三条线段a、b、c,用尺规作出△ABC,使BC=a,AC=b、AB=c.解:作法:1.作线段BC=a;2.以点C为圆心,以b为半径画弧,再以B为圆心,以c为半径画弧,两弧相交于点A;3.连接AC和AB,则△ABC即为所求作的三角形,如图所示.方法总结:已知三角形三边的长,根据全等三角形的判定“SSS”,知三角形的形状和大小也就确定了.作三角形相当于确定三角形三个顶点的位置.因此可先确定三角形的一条边(即两个顶点),再分别以这条边的两个端点为圆心,以已知线段长为半径画弧,两弧的交点即为另一个顶点.三、板书设计1.已知两边及其夹角作三角形2.已知两角及其夹边作三角形3.已知三边作三角形本节课学习了有关三角形的作图,主要包括两种基本作图:作一条线段等于已知线段,作一个角等于已知角.作图时,鼓励学生一边作图,一边用几何语言叙述作法,培养学生的动手能力、语言表达能力

北师大初中八年级数学下册变形后提公因式因式分解教案
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+x(x+1)n(n为正整数).解析:(1)根据已知计算过程直接得出因式分解的方法即可;(2)根据已知分解因式的方法可以得出答案;(3)由(1)中计算发现规律进而得出答案.解:(1)因式分解的方法是提公因式法,共应用了3次;(2)分解因式1+x+x(x+1)+x(x+1)2+…+x(x+1)2015,需应用上述方法2016次,结果是(1+x)2015;(3)1+x+x(x+1)+x(x+1)2+…+x(x+1)n=(1+x)n+1.方法总结:解决此类问题需要认真阅读,理解题意,根据已知得出分解因式的规律是解题关键.三、板书设计1.提公因式分解因式的一般步骤:(1)观察;(2)适当变形;(3)确定公因式;(4)提取公因式.2.提公因式法因式分解的应用本课时是在上一课时的基础上进行的拓展延伸,在教学时要给学生足够主动权和思考空间,突出学生在课堂上的主体地位,引导和鼓励学生自主探究,在培养学生创新能力的同时提高学生的逻辑思维能力.

北师大初中八年级数学下册直接提公因式因式分解教案
解析:(1)首先提取公因式13,进而求出即可;(2)首先提取公因式20.15,进而求出即可.解:(1)39×37-13×91=3×13×37-13×91=13×(3×37-91)=13×20=260;(2)29×20.15+72×20.15+13×20.15-20.15×14=20.15×(29+72+13-14)=2015.方法总结:在计算求值时,若式子各项都含有公因式,用提取公因式的方法可使运算简便.三、板书设计1.公因式多项式各项都含有的相同因式叫这个多项式各项的公因式.2.提公因式法如果一个多项式的各项有公因式,可以把这个公因式提到括号外面,这种因式分解的方法叫做提公因式法.本节中要给学生留出自主学习的空间,然后引入稍有层次的例题,让学生进一步感受因式分解与整式的乘法是逆过程,从而可用整式的乘法检查错误.本节课在对例题的探究上,提倡引导学生合作交流,使学生发挥群体的力量,以此提高教学效果.
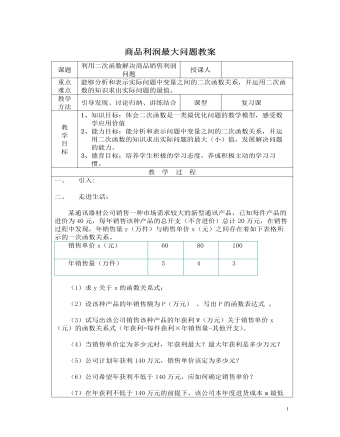
北师大初中九年级数学下册商品利润最大问题2教案
(8)物价部门规定,此新型通讯产品售价不得高于每件80元。在此情况下,售价定为多少元时,该公司可获得最大利润?最大利润为多少万元?若该公司计划年初投入进货成本m不超过200万元,请你分析一下,售价定为多少元,公司获利最大?售价定为多少元,公司获利最少?三、小练兵:某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,销售量y(件)与销售单价x(元)之间的函数关系式为y= –20 x +1800.(1)写出销售该品牌童装获得的利润w(元)与销售单价x(元)之间的函数关系式;(2)若童装厂规定该品牌童装销售单价不低于76元,不高于78元,那么商场销售该品牌童装获得的最大利润是多少元?(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,那么商场销售该品牌童装获得的最大利润是多少元?

北师大初中九年级数学下册解直角三角形1教案
方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.变式训练:见《学练优》本课时练习“课后巩固提升” 第7题【类型三】 构造直角三角形解决面积问题在△ABC中,∠B=45°,AB=2,∠A=105°,求△ABC的面积.解析:过点A作AD⊥BC于点D,根据勾股定理求出BD、AD的长,再根据解直角三角形求出CD的长,最后根据三角形的面积公式解答即可.解:过点A作AD⊥BC于点D,∵∠B=45°,∴∠BAD=45°,∴AD=BD=22AB=22×2=1.∵∠A=105°,∴∠CAD=105°-45°=60°,∴∠C=30°,∴CD=ADtan30°=133=3,∴S△ABC=12(CD+BD)·AD=12×(3+1)×1=3+12. 方法总结:解答此类题目的关键是根据题意构造直角三角形,然后利用所学的三角函数的关系进行解答.

北师大初中九年级数学下册解直角三角形2教案
首先请学生分析:过B、C作梯形ABCD的高,将梯形分割成两个直角三角形和一个矩形来解.教师可请一名同学上黑板板书,其他学生笔答此题.教师在巡视中为个别学生解开疑点,查漏补缺.解:作BE⊥AD,CF⊥AD,垂足分别为E、F,则BE=23m.在Rt△ABE中,∴AB=2BE=46(m).∴FD=CF=23(m).答:斜坡AB长46m,坡角α等于30°,坝底宽AD约为68.8m.引导全体同学通过评价黑板上的板演,总结解坡度问题需要注意的问题:①适当添加辅助线,将梯形分割为直角三角形和矩形.③计算中尽量选择较简便、直接的关系式加以计算.三、课堂小结:请学生总结:解直角三角形时,运用直角三角形有关知识,通过数值计算,去求出图形中的某些边的长度或角的大小.在分析问题时,最好画出几何图形,按照图中的边角之间的关系进行计算.这样可以帮助思考、防止出错.四、布置作业

北师大初中九年级数学下册商品利润最大问题1教案
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?解析:(1)分1≤x<50和50≤x≤90两种情况进行讨论,利用利润=每件的利润×销售的件数,即可求得函数的解析式;(2)利用(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000;当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000.综上所述,y=-2x2+180x+2000(1≤x<50),-120x+12000(50≤x≤90);(2)当1≤x<50时,y=-2x2+180x+2000,二次函数开口向下,对称轴为x=45,当x=45时,y最大=-2×452+180×45+2000=6050;当50≤x≤90时,y=-120x+12000,y随x的增大而减小,当x=50时,y最大=6000.综上所述,销售该商品第45天时,当天销售利润最大,最大利润是6050元.方法总结:本题考查了二次函数的应用,读懂表格信息、理解利润的计算方法,即利润=每件的利润×销售的件数,是解决问题的关键.

北师大初中九年级数学下册圆内接正多边形教案
解析:正多边形的边心距、半径、边长的一半正好构成直角三角形,根据勾股定理就可以求解.解:(1)设正三角形ABC的中心为O,BC切⊙O于点D,连接OB、OD,则OD⊥BC,BD=DC=a.则S圆环=π·OB2-π·OD2=πOB2-OD2=π·BD2=πa2;(2)只需测出弦BC(或AC,AB)的长;(3)结果一样,即S圆环=πa2;(4)S圆环=πa2.方法总结:正多边形的计算,一般是过中心作边的垂线,连接半径,把内切圆半径、外接圆半径、边心距,中心角之间的计算转化为解直角三角形.变式训练:见《学练优》本课时练习“课后巩固提升”第4题【类型四】 圆内接正多边形的实际运用如图①,有一个宝塔,它的地基边缘是周长为26m的正五边形ABCDE(如图②),点O为中心(下列各题结果精确到0.1m).(1)求地基的中心到边缘的距离;(2)已知塔的墙体宽为1m,现要在塔的底层中心建一圆形底座的塑像,并且留出最窄处为1.6m的观光通道,问塑像底座的半径最大是多少?

内蒙古呼和浩特市2016年中考文综(历史部分)真题试题(含解析)
材料 传说神农氏尝百草,首开中医发展先河.甲骨文记载的疾病有数十种,西周时开始分科治病,后期的中医学发展见表: 时期医学家主要成就文化发展阶段先秦扁鹊用针刺、按摩、汤药治疗,采用望、闻、问、切诊断疾病.勃兴秦汉张仲景著作《伤寒杂病论》,阐述中医理论和治病原则.发展、昌盛隋唐孙思邈人称“药王”,著作《千金方》,在医药学史上占有重要地位. 辉煌 明清李时珍著作《本草纲目》广为流传,成为世界医药学的重要文献总结

2015年中考真题精品解析 语文 (山东济南卷) 精编word版(原卷版)
⑦在仰韶文化时期,我国就有了对竹利用的确切记载。竹自竹简、珠笔到竹纸,在保存和传播我们中华民族的古老文化上立下了汗马功劳。以竹为题材的诗词歌赋,用竹编织和雕刻的艺术品,竹制的笙管笛箫奏出的音乐,无不给人类美的享受。⑧在我国文化史上,竹蕴含着中华民族重要的精神价值。人们在长期的劳动实践和文化活动中,把竹的生物特征逐渐升华为一种做人的美德。竹四季常青,不畏逆境,和松、梅并誉为“岁寒三友”;竹中空外直,虚怀若谷,和梅、兰、菊并称为“四君子”。⑨无论是魏晋嵇康、向秀等“竹林七贤”,还是唐朝李白、韩准等“竹溪六逸”,莫不对竹有一份执着和憧憬,清代郑板桥,与竹为邻,以竹为友,爱竹、写竹、画竹、赞竹。“千磨万击还坚韧,任尔东西南北风”,正是他坚忍不拔、超凡脱俗的人格写照。

2015年中考真题精品解析 语文(黑龙江大庆卷)精编word版(原卷版)
①2014年年中,世界卫生组织(WHO)公布了《2013年全球气候状况报告》。报告显示,2013年全球陆地和海洋表面平均温度为14.5℃,比1961-1990年的平均温度升高0.5℃。自有温度记录以来,全球14个最热年份中有13个出现在本世纪,而过去30年中每个10年都比前十年更热。②厄尔尼诺是发生在热带太平洋上海温异常增暖的气候现象,大范围热带太平洋增暖会造成全球气候变化。进入20世纪70年代后,全球出现的异常天气,都有范围广、灾情重、时间长等特点,而在这一系列异常天气的背后,厄尔尼诺暖流都起着重要作用。

广西玉林市、防城港市2015年中考语文真题试题(含答案)
那天的晚饭、吴老师一直给我夹莱、夸我作丈修改得好,还说我各方面都有进步,下个学期能进班委会、我熟械地吃着饭、饭菜是什么味道却没留下一点印象,不知道为为什么,我高兴不起来。一个月后,学校在通告栏里用一整张红纸发布了喜报,庆祝我校学生第一次在全县小学文竞赛中获二等奖。全班都拉我去看,我那篇作文竟然真的得了奖。我死活都不肯去,小利说我脸都红了。害羞吗?当然不是,谦虚吗?更不是。可是第二天的全校表彰会、我就躲不过去了,那次大会本来是表彰上学期的优秀学生的,没想到,最后是隆重给我颁发作文二等奖,我想找个地缝钻进去都来及。在全校师生面前,我捧着大红面的获奖证书、奖品,却低着头,像犯了错误。校长亲自给我颁奖之后,还宣布本学期每周一的全校升旗仪式由我来领队。不知怎的,我突然放声大哭。吴老师带着在台下拼命鼓掌。大家都很感动,觉得我是真情流露,是激动。可是谁也不会相信,我真不激动,而是莫名其妙地羞愧难当。我觉得那篇作文跟我一点关系也没有,可是每个字又的确是我写的。那种感觉,我怎么也说不清楚。(选自《小小说选刊》2015年第3期)

新疆乌鲁木齐市2017年中考语文真题试题(含答案)
直到今天,我依旧最喜欢一个姓,高;最喜欢一个字,翔;超喜欢一个词儿,高翔。抬头,天蓝云白,鸟儿高翔,再没有比这更美的意境了。回眸,凝视,三十年前清晰如昨。记得是个午自习,我们刚升入初三的第二周。正在做作业,突然听见几声响亮的击掌,用脚趾头想想都知道是老班。

2016年中考真题精品解析 语文(山东济南卷)精编word版(原卷版)
青蒿素治疗疟疾效果显著,是抵抗疟疾耐药性最好的药物。中国发现青蒿素时,美国也研制出一种抗疟新药—化学合成的甲氟喹,但疟原虫很快就适应了它,产生耐药性,临床使用后患者还出现了明显的不良反应。而对于青蒿素这种从中草药中提取的药物,疟原虫对它完全没有抵抗能力。1976 年1月,柬埔寨爆发疟疾,因疟原虫已经产生耐药性,疫情一时难以控制。中国医疗队携带一批青蒿素在柬埔寨大显神威,挽救了一大批疟疾患者的生命。

2021年内蒙古包头市、巴彦淖尔市中考语文真题(解析版)
2020年,联合国发布了一份关于全球气候变化的报告。报告指出,由于气候变化,全球各地的冰原和冰川发生减少。2006年至2015年,平均每年全球海平面上升至少3.6毫米。2020年上半年,二氧化碳等温室气体浓度达到了三百万年以来的最高水平,并且还在持续上升。

广西北部湾经济开发区2021年中考语文试题(原卷版)
许慎的《说文》中讲:“亭,亭也,人所停集也。凡驿亭、邮亭、园亭,并取此义为名。”亭的历史十分悠久,一直可以上溯到商周以前。但是亭字的出现,却相对较晚,大致始于春秋战国前后。甲骨文,金文中均未见有亭字,现在发现的最早的亭字,是先秦时期的古陶文和古玺文。因此,在秦以前,亭的基本形制或许并不是十分成熟,但是到秦汉时,亭已经十分普遍了,是一种有着多种用途,实用性很强的建筑。

