-

人教版高中政治必修3源远流长的中华文化精品教案
(一)知识目标(1)识记中华 文化源远流长的主要见证是文字和史学典籍 ,文字的作用、意义 ,史学典籍 ,中华文化的包容性。(2)说明中华文化源远流长的发展过程,是世界上唯一没有中断的文明 ,汉字与史学典籍是中华文化源远流长和见证,如何再创中华文化新的辉煌(3)分析说明中华文化源远流长,是当今世界上唯一没有中断的文明(二)能力目标通过学生课外探究、信息资源的收集整合,培养学生的信息素养、实践能力,激发学生的生活智慧与学习智慧、时代创新精神与团队合作精神。培养同学们综合思维能力,全面、辩证、历史地分析中华文化的基本特征。培养同学们辩证分析能力,辨析中华文化的区域特征,说明中华文化是中国各族人民共同创造的;展现源远流长的中华文化是中华民族延续和发展的重要标识。
初中化学人教版九年级下册《实验活动7溶液酸碱性的检验》教案
1.自己选择植物的花瓣(牵牛花、月季花)、蔬菜(紫卷心菜、胡萝卜) 在研钵中捣烂,加入酒精(它有消毒作用,可使制得的指示剂长期 保存)浸泡,用纱布将浸泡出的汁液过滤或挤出,就得到指示剂, 2.把制好的指示剂装入试剂瓶,贴上标签备用。 把食醋、稀盐酸、稀氢氧化钠、澄清石灰水,分别滴在两个 白色点滴板上,用石蕊、酚酞分别滴在上述溶液上,通过颜 色变化检验它们的酸碱性。 用玻璃棒分别蘸取上述溶液,滴在pH试纸上,然后对照标准 比色卡比较,得出pH值,也就是酸碱度。 把上述溶液滴在白色点滴板上,用滴管吸一下你自制的指示剂,滴在滴板的溶液里,观察颜色变化,每用一种指示剂,换一下滴板的溶液。 把所得到颜色变色变化的信息和pH值数据填入教材第70页的表中。 3.取少量土壤样品,将土壤样品与蒸馏水按1∶5的质量比在烧杯中混合, 充分搅拌后静置,用玻璃棒蘸澄清的液体,滴在pH试纸上,然后对照 标准比色卡记录读数。

人教版高中地理必修1自然地理环境的差异性教案
注:号码代表自然带类型【讨论问题】(1)请将板图中符号与你所在的自然带“对号入座”(提问几位同学)。(2)哪些属于温带森林?哪些属于热带森林?(3)南半球缺少哪些自然带?(4)气 候类型相同而自然带不同的是哪种气候类型,哪些自然带?(5)自然带相同,气候类型不同的是哪种自然带,哪些气候类型?(6)两组同学“通道”之间所处的是什么自然带?(答:过渡带,说明自然带没有严格界线,整个自然界是非常和谐地过渡、相互联系结成的有机整体)。【放录像片】《各自然带景观》,看一段录像增加感性认识(教师可以使用自己编辑的录像资料)。【学生讨论】阅读课本P98“世界陆地自然带分布图”了解自然 带的基本分布情况:【学生回答】略。【教师总结】

高教版中职数学基础模块下册:8.2《直线的方程》教学设计
课程名称数学课题名称8.2 直线的方程课时2授课日期2016.3任课教师刘娜目标群体14级五高班教学环境教室学习目标知识目标: (1)理解直线的倾角、斜率的概念; (2)掌握直线的倾角、斜率的计算方法. 职业通用能力目标: 正确分析问题的能力 制造业通用能力目标: 正确分析问题的能力学习重点直线的斜率公式的应用.学习难点直线的斜率概念和公式的理解.教法、学法讲授、分析、讨论、引导、提问教学媒体黑板、粉笔

高教版中职数学基础模块下册:9.1《平面的基本性质》教学设计
课题序号 授课班级 授课课时2授课形式新课授课章节 名称§9-1 平面基本性质使用教具多媒体课件教学目的1.了解平面的定义、表示法及特点,会用符号表示点、线、面之间的关系—基础模块 2.了解平面的基本性质和推论,会应用定理和推论解释生活中的一些现象—基础模块 3.会用斜二测画法画立体图形的直观图—基础模块 4.培养学生的空间想象能力教学重点用适当的符号表示点、线、面之间的关系;会用斜二测画法画立体图形的直观图教学难点从平面几何向立体几何的过渡,培养学生的空间想象能力.更新补充 删节内容 课外作业 教学后记能动手画,动脑想,但立体几何的语言及想象能力差
高教版中职数学基础模块下册:6.1《数列的概念》教案设计
【教学目标】1. 理解数列的通项公式的意义,能根据通项公式写出数列的任意一项,以及根据其前几项写出它的一个通项公式.2. 了解数列的递推公式,会根据数列的递推公式写出前几项.3.培养学生积极参与、大胆探索的精神,培养学生的观察、分析、归纳的能力.教学重点 数列的通项公式及其应用.教学难点 根据数列的前几项写出满足条件的数列的一个通项公式.教学方法 本节课主要采用例题解决法.通过列举实例,进一步研究数列的项与序号之间的关系.通过三类题目,使学生深刻理解数列通项公式的意义,为以后学习等差数列与等比数列打下基础.【教学过程】 环节教学内容师生互动设计意图导 入⒈数列的定义 按一定次序排列的一列数叫做数列. 注意:(1)数列中的数是按一定次序排列的; (2)同一个数在数列中可以重复出现. 2. 数列的一般形式 数列a1,a2,a3,…,an,…,可记作{ an }. 3. 数列的通项公式: 如果数列{ an }的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式. 教师引导学生复习. 为学生进一步理解通项公式,应用通项公式解决实际问题做好准备.

【高教版】中职数学拓展模块:1.1《两角和与差的正弦公式与余弦公式》教案
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 1.1两角和与差的余弦公式与正弦公式. *创设情境 兴趣导入 问题 我们知道,显然 由此可知 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 10*动脑思考 探索新知 在单位圆(如上图)中,设向量、与x轴正半轴的夹角分别为和,则点A的坐标为(),点B的坐标为(). 因此向量,向量,且,. 于是 ,又 , 所以 . (1) 又 (2) 利用诱导公式可以证明,(1)、(2)两式对任意角都成立(证明略).由此得到两角和与差的余弦公式 (1.1) (1.2) 公式(1.1)反映了的余弦函数与,的三角函数值之间的关系;公式(1.2)反映了的余弦函数与,的三角函数值之间的关系. 总结 归纳 仔细 分析 讲解 关键 词语 思考 理解 记忆 启发引导学生发现解决问题的方法 25

高教版中职数学基础模块下册:8.3《两条直线的位置关系》教案设计
教 学 过 程教师 行为学生 行为教学 意图 *揭示课题 8.3 两条直线的位置关系(二) *创设情境 兴趣导入 【问题】 平面内两条既不重合又不平行的直线肯定相交.如何求交点的坐标呢? 图8-12 介绍 质疑 引导 分析 了解 思考 启发 学生思考 *动脑思考 探索新知 如图8-12所示,两条相交直线的交点,既在上,又在上.所以的坐标是两条直线的方程的公共解.因此解两条直线的方程所组成的方程组,就可以得到两条直线交点的坐标. 观察图8-13,直线、相交于点P,如果不研究终边相同的角,共形成四个正角,分别为、、、,其中与,与为对顶角,而且. 图8-13 我们把两条直线相交所成的最小正角叫做这两条直线的夹角,记作. 规定,当两条直线平行或重合时,两条直线的夹角为零角,因此,两条直线夹角的取值范围为. 显然,在图8-13中,(或)是直线、的夹角,即. 当直线与直线的夹角为直角时称直线与直线垂直,记做.观察图8-14,显然,平行于轴的直线与平行于轴的直线垂直,即斜率为零的直线与斜率不存在的直线垂直. 图8-14 讲解 说明 讲解 说明 引领 分析 仔细 分析 讲解 关键 词语 思考 思考 理解 思考 理解 记忆 带领 学生 分析 带领 学生 分析 引导 式启 发学 生得 出结 果

人教版高中地理必修2人口的空间变化精品教案
经济因素对人口迁移是主要的,经常起作用的因素,是人口迁移的基本动因。通常情况下,经济发展水平的差异决定着人们迁移的方向,人们迁移是为了追求更好的就业机会和更高的经济收入。经济发展水平高的地区往往成为人口迁入地,人口的迁移量取决于迁入地对劳动力的需求状况和迁出地人口相对过剩的状况。师:20世纪80年代深圳、珠海等地设立了经济特区’吸I了大量的人口迁入。这又说明了什么问题? (生回答,师总结)从宏观上看,经济布局也会造成大量的人口迁移。说明经济越发达,对人口的吸引力(即拉力)越大。经济发展水平、规模和速度决定着人口迁移的流向、流量和流速。师:交通和通讯又如何影响着人口的迁移呢?生:交通和通讯的发展,缩小了地区之间的距离,促进了人口迁移。
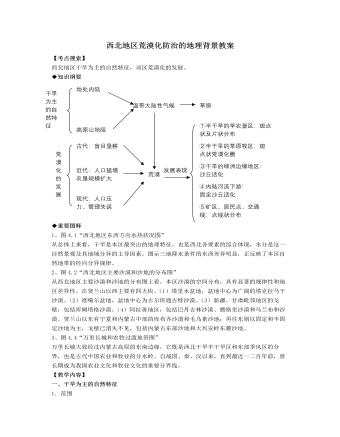
人教版高中地理选修2西北地区荒漠化防治的地理背景教案
【知能训练】一、选择题(第1-4题为单项选择题,第5-6题为双项选择题)1、斑点状土地荒漠化圈主要分布的地方是()A.塔里木河下游绿洲B.呼伦贝尔草原和锡林郭勒草原C.居民点、工矿区及交通线附近D.科尔沁沙地2、近年来,西北地区环境发展的趋势是A.随着人口增加和经济发展,绿洲环境总体趋于好转B.风沙活动增强,盐碱地面积增加C.绿洲经济以农业为主,无环境污染问题D.随着人类对环境影响的加强,绿洲环境向良性方向发展3、我国沙漠沙地所处纬度最高的是()A.科尔沁沙地B.呼伦贝尔沙地C.古尔班通古特沙漠D.乌兰布和沙漠4、我国西北地区干旱为主的自然景观的主要成因是()A.地处北半球亚洲高压的范围之内B.地处东南季风的背风坡C.深居内陆又隔崇山峻岭D.气候干旱、植被稀少、河短水少

人教A版高中数学必修二复数的三角表示教学设计
本节内容是复数的三角表示,是复数与三角函数的结合,是对复数的拓展延伸,这样更有利于我们对复数的研究。1.数学抽象:利用复数的三角形式解决实际问题;2.逻辑推理:通过课堂探究逐步培养学生的逻辑思维能力;3.数学建模:掌握复数的三角形式;4.直观想象:利用复数三角形式解决一系列实际问题;5.数学运算:能够正确运用复数三角形式计算复数的乘法、除法;6.数据分析:通过经历提出问题—推导过程—得出结论—例题讲解—练习巩固的过程,让学生认识到数学知识的逻辑性和严密性。复数的三角形式、复数三角形式乘法、除法法则及其几何意义旧知导入:问题一:你还记得复数的几何意义吗?问题二:我们知道,向量也可以由它的大小和方向唯一确定,那么能否借助向量的大小和方向这两个要素来表示复数呢?如何表示?

人教A版高中数学必修一三角函数的应用教学设计(2)
本节课是在学习了三角函数图象和性质的前提下来学习三角函数模型的简单应用,进一步突出函数来源于生活应用于生活的思想,让学生体验一些具有周期性变化规律的实际问题的数学“建模”思想,从而培养学生的创新精神和实践能力.课程目标1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.2.实际问题抽象为三角函数模型. 数学学科素养1.逻辑抽象:实际问题抽象为三角函数模型问题;2.数据分析:分析、整理、利用信息,从实际问题中抽取基本的数学关系来建立数学模型; 3.数学运算:实际问题求解; 4.数学建模:体验一些具有周期性变化规律的实际问题的数学建模思想,提高学生的建模、分析问题、数形结合、抽象概括等能力.
人教A版高中数学必修二总体离散程度的估计教学设计
问题二:上述问题中,甲、乙的平均数、中位数、众数相同,但二者的射击成绩存在差异,那么,如何度量这种差异呢?我们可以利用极差进行度量。根据上述数据计算得:甲的极差=10-4=6 乙的极差=9-5=4极差在一定程度上刻画了数据的离散程度。由极差发现甲的成绩波动范围比乙的大。但由于极差只使用了数据中最大、最小两个值的信息,所含的信息量很少。也就是说,极差度量出的差异误差较大。问题三:你还能想出其他刻画数据离散程度的办法吗?我们知道,如果射击的成绩很稳定,那么大多数的射击成绩离平均成绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击成绩离平均成绩会比较远。因此,我们可以通过这两组射击成绩与它们的平均成绩的“平均距离”来度量成绩的波动幅度。

《百年风华启新程,以史为鉴创未来》国旗下的讲话范文
大家好!我是xxxx,今天我演讲的题目是《百年风华启新程,以史为鉴创未来》。 “世之奇伟、瑰怪,非常之观,常在于险远”,唯有以青春作注,不断探索开辟新发现,勇于走在时代前列,才能发现常人所目不及的新事物,才不会因虚度年华而悔恨,因碌碌无为而羞耻。 当国泰民安,丰衣足食,当国家强盛,傲视群雄,中国的青年在顺境中逆风而走,在平安中奔赴隐藏的危难。“以青春之我,创造青春之家庭,青春之国家,青春之民族”。北大90后学子宋玺,剪掉长发,穿上戎装,正姿护航亚丁湾;22岁抗疫医生李思思,用生命践行了对祖国的铮铮誓言;26岁年轻调度员高健,用一声声“北京明白”证明着征途是星辰大海…… 一代人又一代人的长征,一代人又一代人的担当。过往几代青年,皆以梦为马,以铁肩担道义,以不断探索中华之未来的脚步,铸就了如今这伟大的时代。青年的发展应该与时代环境同向而行,同频共振,时代昂扬向上的曲线,即是中国青年的生命轨迹。时间是变化的标尺,空间是更迭的参照,时空为证,见证了发展飞跃向前。每个时代有每个时代的气质,一代人有一代人的使命。但英雄从未远去,精神从不过时。无论是为抗击新冠肺炎疫情献出生命的医护人员,还是将生命定格在脱贫攻坚征程上的扶贫干部,在他们身上,同样矗立着直冲霄汉的英风浩气。

《点滴铸就成功,习惯成就未来》国旗下的讲话范文
我今天讲话的题目是“点滴铸就成功,习惯成就未来”,生活中,我们仰慕优秀的人,我们都渴望自己也成为一个优秀的人,但又似乎感觉优秀是一个遥不可及的目标,很难达到。其实,优秀离我们并不遥远,优秀体现在你我的一言一行之中,体现在一件件不起眼的小事之中。著名教育家叶圣陶先生说过这样一句话:“什么是教育?简单一句话,就是要养成习惯。”我们在学校,不仅要学好科学文化知识,更要进行能力培养,良好习惯的养成。怎样培养自己的好习惯?首先需要检查一下自己,反省一下自身的一些坏习惯。你是否留意到居家学习的这段时间以来,时间总是不知不觉中就过去了?我们刚打开书本想要认真学习,突然被旁边的琐碎事情吸引了注意力,就无法再专心学习?这一些都是阻止我们变优秀的坏习惯。那我们应该如何改正自己的缺点,培养良好的行为习惯呢?简单来说就是用好习惯代替坏习惯,这里给大家几点建议:
人教A版高中数学必修二总体取值规律的估计教学设计
可以通过下面的步骤计算一组n个数据的第p百分位数:第一步:按从小到大排列原始数据;第二步:计算i=n×p%;第三步:若i不是整数,而大于i的比邻整数位j,则第p百分位数为第j项数据;若i是整数,则第p百分位数为第i项与第i+1项的平均数。我们在初中学过的中位数,相当于是第50百分位数。在实际应用中,除了中位数外,常用的分位数还有第25百分位数,第75百分位数。这三个分位数把一组由小到大排列后的数据分成四等份,因此称为四分位数。其中第25百分位数也称为第一四分位数或下四分位数等,第75百分位数也称为第三四分位数或上四分位数等。另外,像第1百分位数,第5百分位数,第95百分位数,和第99百分位数在统计中也经常被使用。例2、根据下列样本数据,估计树人中学高一年级女生第25,50,75百分位数。

(12月5日国际志愿者日)国旗下讲话:让爱洒满世界的每一个角落
谈到志愿者,相信大家并不陌生。联合国将它定义为“不以利益、金钱、扬名为目的,而是为了近邻乃至全世界进行贡献的活动者”,并于1985年12月17日,第40届联合国大会上,把每年12月5日定为“国际志愿者日”,目的是为了在全世界范围内弘扬志愿者精神。如今已有100多个国家积极响应,我国也在此之列。中国是礼仪之邦,自古就有“君子贵人贱己,先人而后己”之说,依靠自己的力量去帮助他人,将爱的温暖在人与人之间传递,让社会更和谐,这本身也是个人价值的社会体现,又何乐而不为呢?我们都还记得那不平凡的XX年,中国经历的年初的特大雪灾,地震和8月在京举行的奥林匹克运动会。这些考验,向全世界展示了一个崛起强国的巨大力量,和国人伟大的民族精神。在这些重大事件中,都可以见到活跃着的一些身影,是的,他们是志愿者。他们奋不顾身赶赴灾区,运输救灾物质,帮助受难群众。他们不计名利,默默奉献,为人们重建家园,他们用爱心、关怀、抚慰人们受伤的心灵。他们以热情、礼貌、智慧向来自四面八方的宾朋展示中国的魅力。当我们再回想起这一幕幕场景时,怎能忘记这些可爱的志愿者们,所付出的一切呢?

(校长)国旗下讲话:《做一个“崇尚廉洁、诚信守法”的好少年》
同学们,听说过《两袖清风》这个成语故事吗?这个成语故事说的是明朝正统年间,宦官王振以权谋私,每逢朝会,各地官僚为了讨好他,都献以珠宝白银,巡抚于谦每次进京奏事,总是不带任何礼品。他的同僚劝他说:“你虽然不献金宝、攀求权贵,也应该带一些著名的土特产如线香、蘑菇、手帕等物,送点人情呀!”于谦笑着举起两袖,风趣地说:“带有清风!”以示对那些阿谀奉承之贪官的嘲弄。两袖清风的成语从此便流传下来。古往今来,有多少清正廉洁、务实为民的清官受到百姓的崇敬与爱戴,他们的形象深入人心,他们的故事久久传颂。一代清官包公、海瑞的故事热映荧屏,久演不衰;人民公仆孔繁森、牛玉儒、任长霞的事迹震撼人心,影响甚广。是的,无论历史如何变迁,无论时代怎样发展,廉洁永远是时代的呼唤,廉洁永远是人民的期盼。

(新任校长)国旗下讲话:让自己的成长因进取而健康
因徐校长退休,上个星期我来到了学校,又成为了东山实验小学的一员,担任校长工作。我姓吴,以后大家可以叫我吴校长或吴老师。在13年前,我就是我们学校的数学老师。在这里我工作了整整20年,我的儿子也是在本校毕业。这是一所了不起的小学,是XX省首批办好的老牌实验小学,也是XX省“模范学校”。这是一所办学近200年的学校,多少年来为中学输送了一批批优秀的毕业生,为生国家培养了一大批优秀的人才,院士、科学家等数以百计。我的儿子后来也考取了北京大学,现在国家公派在国外留学。我说儿子并不是自我夸耀,而是想告诉同学们一点,能在东山实验小学学习与工作是幸福的、光荣的。因为,东山实验小学有一个个关爱你们,为同学们的获得良好的学习成长、优良的品德形成,健康的身心发展的敬业、爱岗、乐于奉献的老师。在此我建议,让我们用最热烈的掌声向老师们表示最衷心的感谢!

“世界艾滋病日”国旗下的讲话:增强自我保护意识
作为一个青少年,应该认识到:艾滋病的传播没有国界,我国是世界上的人口大国,是国际社会的一员,有责任和世界各国携手共同努力控制艾滋病的蔓延;学习预防艾滋病的知识,不仅使青少年能及时了解与掌握预防艾滋病的知识、增强自我保护意识和抵御艾滋病侵袭的能力;更重要的是培养预防艾滋病的社会责任感、使命感。青少年是社会和国家的未来,是全社会预防艾滋病的主力军。青少年参与预防艾滋病的活动意义深远,不仅是为了青少年自己的生存与健康,而且是为了全社会、全人类的发展。青少年有责任成为抵御艾滋病在二十一世纪猖獗流行的最有生气的社会力量。