-

人教版高中语文必修3《学会宽容 学习选择和使用论据》教案2篇
评价分析法,就是引述事例后,对所引述的事例作适当的评价,从而使自己的观点得到印证。例如,在论“节俭”时,引用了“曾国藩以俭戒子,其子曾纪泽终成出色的外交家;方志敏居官不贪,一生清贫,千古留名”的事实后,接着进行分析:是的,“俭者心常富”,节俭能培养人同困难作斗争的勇气和意志,而这正是一个人立业最重要的素质。从这个意义上说,有人说饥饿是人生的佐料,吃苦是一种资本也不无道理,而自觉和戒奢尚俭则更是促人修身养性,磨炼意志的有效途径。这里,作者紧扣论点,对论据进行了评价性分析,这种评价分析使作者的观点得到强化。(四)因果分析法因果分析法,就是抓住论据所述的事实,并据此推求形成原因的一种分析方法。事出必有其因。我们可以依据事物发展变化的因果关系,由事物发展变化的结果,推导出产生这种结果的原因,从而揭示出一定的生活规律,使事例有力地证明观点。
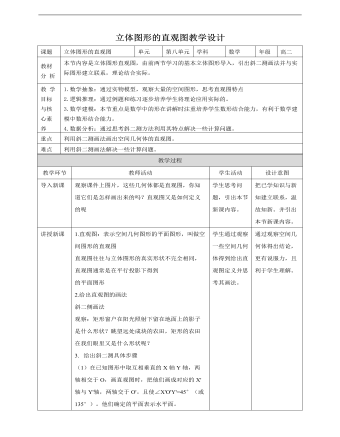
人教A版高中数学必修二立体图形直观图教学设计
1.直观图:表示空间几何图形的平面图形,叫做空间图形的直观图直观图往往与立体图形的真实形状不完全相同,直观图通常是在平行投影下得到的平面图形2.给出直观图的画法斜二侧画法观察:矩形窗户在阳光照射下留在地面上的影子是什么形状?眺望远处成块的农田,矩形的农田在我们眼里又是什么形状呢?3. 给出斜二测具体步骤(1)在已知图形中取互相垂直的X轴Y轴,两轴相交于O,画直观图时,把他们画成对应的X'轴与Y'轴,两轴交于O'。且使∠X'O'Y'=45°(或135°)。他们确定的平面表示水平面。(2)已知图形中平行于X轴或y轴的线段,在直观图中分别画成平行于X'轴或y'轴的线段。(3)已知图形中平行于X轴的线段,在直观图中保持原长度不变,平行于Y轴的线段,在直观图中长度为原来一半。4.对斜二测方法进行举例:对于平面多边形,我们常用斜二测画法画出他们的直观图。如图 A'B'C'D'就是利用斜二测画出的水平放置的正方形ABCD的直观图。其中横向线段A'B'=AB,C'D'=CD;纵向线段A'D'=1/2AD,B'C'=1/2BC;∠D'A'B'=45°,这与我们的直观观察是一致的。5.例一:用斜二测画法画水平放置的六边形的直观图(1)在六边形ABCDEF中,取AD所在直线为X轴,对称轴MN所在直线为Y轴,两轴交于O',使∠X'oy'=45°(2)以o'为中心,在X'上取A'D'=AD,在y'轴上取M'N'=½MN。以点N为中心,画B'C'平行于X'轴,并且等于BC;再以M'为中心,画E'F'平行于X‘轴并且等于EF。 (3)连接A'B',C'D',E'F',F'A',并擦去辅助线x轴y轴,便获得正六边形ABCDEF水平放置的直观图A'B'C'D'E'F' 6. 平面图形的斜二测画法(1)建两个坐标系,注意斜坐标系夹角为45°或135°;(2)与坐标轴平行或重合的线段保持平行或重合;(3)水平线段等长,竖直线段减半;(4)整理.简言之:“横不变,竖减半,平行、重合不改变。”
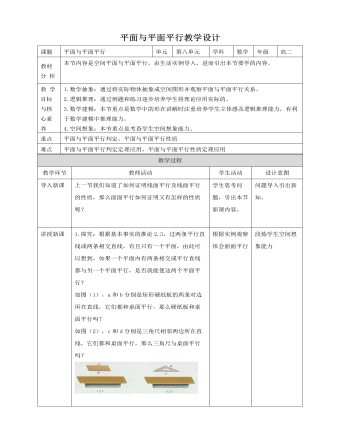
人教A版高中数学必修二平面与平面平行教学设计
1.探究:根据基本事实的推论2,3,过两条平行直线或两条相交直线,有且只有一个平面,由此可以想到,如果一个平面内有两条相交或平行直线都与另一个平面平行,是否就能使这两个平面平行?如图(1),a和b分别是矩形硬纸板的两条对边所在直线,它们都和桌面平行,那么硬纸板和桌面平行吗?如图(2),c和d分别是三角尺相邻两边所在直线,它们都和桌面平行,那么三角尺与桌面平行吗?2.如果一个平面内有两条平行直线与另一个平面平行,这两个平面不一定平行。我们借助长方体模型来说明。如图,在平面A’ADD’内画一条与AA’平行的直线EF,显然AA’与EF都平行于平面DD’CC’,但这两条平行直线所在平面AA’DD’与平面DD’CC’相交。3.如果一个平面内有两条相交直线与另一个平面平行,这两个平面是平行的,如图,平面ABCD内两条相交直线A’C’,B’D’平行。

人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.③符号语言:任意a?α,都有l⊥a?l⊥α.
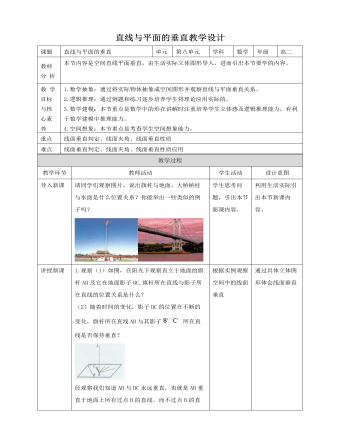
人教A版高中数学必修二直线与平面垂直教学设计
1.观察(1)如图,在阳光下观察直立于地面的旗杆AB及它在地面影子BC,旗杆所在直线与影子所在直线的位置关系是什么?(2)随着时间的变化,影子BC的位置在不断的变化,旗杆所在直线AB与其影子B’C’所在直线是否保持垂直?经观察我们知道AB与BC永远垂直,也就是AB垂直于地面上所有过点B的直线。而不过点B的直线在地面内总是能找到过点B的直线与之平行。因此AB与地面上所有直线均垂直。一般地,如果一条直线与一个平面α内所有直线均垂直,我们就说l垂直α,记作l⊥α。2.定义:①文字叙述:如果直线l与平面α内的所有 直线都垂直,就说直线l与平面α互相垂直,记作l⊥α.直线l叫做平面α的垂线,平面α叫做直线l的垂面.直线与平面垂直时,它们唯一的公共点P叫做交点.②图形语言:如图.画直线l与平面α垂直时,通常把直线画成与表示平面的平行四边形的一边垂直.
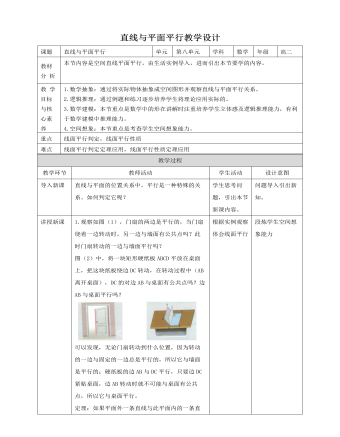
人教A版高中数学必修二直线与直线垂直教学设计
6.例二:如图在正方体ABCD-A’B’C’D’中,O’为底面A’B’C’D’的中心,求证:AO’⊥BD 证明:如图,连接B’D’,∵ABCD-A’B’C’D’是正方体∴BB’//DD’,BB’=DD’∴四边形BB’DD’是平行四边形∴B’D’//BD∴直线AO’与B’D’所成角即为直线AO’与BD所成角连接AB’,AD’易证AB’=AD’又O’为底面A’B’C’D’的中心∴O’为B’D’的中点∴AO’⊥B’D’,AO’⊥BD7.例三如图所示,四面体A-BCD中,E,F分别是AB,CD的中点.若BD,AC所成的角为60°,且BD=AC=2.求EF的长度.解:取BC中点O,连接OE,OF,如图。∵E,F分别是AB,CD的中点,∴OE//AC且OE=1/2AC,OF//AC且OF=1/2BD,∴OE与OF所成的锐角就是AC与BD所成的角∵BD,AC所成角为60°,∴∠EOF=60°或120°∵BD=AC=2,∴OE=OF=1当∠EOF=60°时,EF=OE=OF=1,当∠EOF=120°时,取EF的中点M,连接OM,则OM⊥EF,且∠EOM=60°∴EM= ,∴EF=2EM=

人教版高中数学选择性必修二变化率问题教学设计
导语在必修第一册中,我们研究了函数的单调性,并利用函数单调性等知识,定性的研究了一次函数、指数函数、对数函数增长速度的差异,知道“对数增长” 是越来越慢的,“指数爆炸” 比“直线上升” 快得多,进一步的能否精确定量的刻画变化速度的快慢呢,下面我们就来研究这个问题。新知探究问题1 高台跳水运动员的速度高台跳水运动中,运动员在运动过程中的重心相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+4.8t+11.如何描述用运动员从起跳到入水的过程中运动的快慢程度呢?直觉告诉我们,运动员从起跳到入水的过程中,在上升阶段运动的越来越慢,在下降阶段运动的越来越快,我们可以把整个运动时间段分成许多小段,用运动员在每段时间内的平均速度v ?近似的描述它的运动状态。

人教版高中数学选修3离散型随机变量及其分布列(1)教学设计
4.写出下列随机变量可能取的值,并说明随机变量所取的值表示的随机试验的结果.(1)一个袋中装有8个红球,3个白球,从中任取5个球,其中所含白球的个数为X.(2)一个袋中有5个同样大小的黑球,编号为1,2,3,4,5,从中任取3个球,取出的球的最大号码记为X.(3). 在本例(1)条件下,规定取出一个红球赢2元,而每取出一个白球输1元,以ξ表示赢得的钱数,结果如何?[解] (1)X可取0,1,2,3.X=0表示取5个球全是红球;X=1表示取1个白球,4个红球;X=2表示取2个白球,3个红球;X=3表示取3个白球,2个红球.(2)X可取3,4,5.X=3表示取出的球编号为1,2,3;X=4表示取出的球编号为1,2,4;1,3,4或2,3,4.X=5表示取出的球编号为1,2,5;1,3,5;1,4,5;2,3,5;2,4,5或3,4,5.(3) ξ=10表示取5个球全是红球;ξ=7表示取1个白球,4个红球;ξ=4表示取2个白球,3个红球;ξ=1表示取3个白球,2个红球.

人教版高中数学选修3分类变量与列联表教学设计
一、 问题导学前面两节所讨论的变量,如人的身高、树的胸径、树的高度、短跑100m世界纪录和创纪录的时间等,都是数值变量,数值变量的取值为实数.其大小和运算都有实际含义.在现实生活中,人们经常需要回答一定范围内的两种现象或性质之间是否存在关联性或相互影响的问题.例如,就读不同学校是否对学生的成绩有影响,不同班级学生用于体育锻炼的时间是否有差别,吸烟是否会增加患肺癌的风险,等等,本节将要学习的独立性检验方法为我们提供了解决这类问题的方案。在讨论上述问题时,为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.分类变量的取值可以用实数表示,例如,学生所在的班级可以用1,2,3等表示,男性、女性可以用1,0表示,等等.在很多时候,这些数值只作为编号使用,并没有通常的大小和运算意义,本节我们主要讨论取值于{0,1}的分类变量的关联性问题.

人教版高中数学选修3离散型随机变量及其分布列(2)教学设计
温故知新 1.离散型随机变量的定义可能取值为有限个或可以一一列举的随机变量,我们称为离散型随机变量.通常用大写英文字母表示随机变量,例如X,Y,Z;用小写英文字母表示随机变量的取值,例如x,y,z.随机变量的特点: 试验之前可以判断其可能出现的所有值,在试验之前不可能确定取何值;可以用数字表示2、随机变量的分类①离散型随机变量:X的取值可一、一列出;②连续型随机变量:X可以取某个区间内的一切值随机变量将随机事件的结果数量化.3、古典概型:①试验中所有可能出现的基本事件只有有限个;②每个基本事件出现的可能性相等。二、探究新知探究1.抛掷一枚骰子,所得的点数X有哪些值?取每个值的概率是多少? 因为X取值范围是{1,2,3,4,5,6}而且"P(X=m)"=1/6,m=1,2,3,4,5,6.因此X分布列如下表所示

音乐老师钢琴老师艺术老师简历
220xx.01 -20xx.12 广州XXX智慧少年宫 职位:音乐老师工作描述:根据课程教案、教学视频等,为学员提供专业的钢琴、合唱、歌唱表演等兴趣学习体验;带动学员达成课程目标;指导智慧少年宫学生参加比赛或汇演活动;配合教务部门,与学生和家长保持良好沟通;组织学员参加智慧少年宫组织的相关比赛或汇演活动。

公司管理制度(适用于信息技术公司)
一、董事会职责1、负责召集股东会,并向股东报告工作;2、执行股东会的决议;3、审定公司的经营计划和投资方案;4、制订公司的年度财务预算方案;5、制订公司的利润分配方案和弥补亏损方案;6、制订公司增加或者减少注册资本方案;7、拟订公司合并、分立、变更公司形式、解散的方案;8、决定公司内部管理机构的设置;二、综合管理部基本工作职责1、行政事务:⑴ 拟定公司行政管理制度并监督实施;⑵ 公司会议管理;⑶ 档案管理;⑷ 印章管理;⑸ 合同管理;⑹ 办公设备及办公用品采买和管理;⑺ 车辆管理;⑻ 消防、安全卫生管理;⑼ 资产管理;⑽ 公司经营所需的各种信息资源管理;⑾ 公司对外关系管理;⑿ 公司各项年检工作;⒀ 企业文化建设及企业形象策划;⒁ 完成总经理及副总经理交办的其他任务。2、人事管理事务:综合管理部的人事职责是负责公司各级员工的聘用、考核、监察、调动、离职、社会保险等。具体职责如下:⑴ 组织拟定公司各机构的人员编制计划;⑵ 负责公司各职位薪酬规划、福利制度制订与修订;⑶ 负责公司人员选聘、考核、监察、调动等工作;⑷ 对拟招聘的公司人员进行面试调查,并办理有关入职手续;⑸ 办理人员任免、调薪、迁调、奖惩等各项事务;⑹ 负责公司员工劳动合同、社会保险、请假等工作;⑺ 定期组织对员工的考核、评议;⑼ 员工考勤管理及劳动纪律管理;⑿ 负责落实执行公司的各种规章制度;⒀ 完成领导交办的其他任务。三、财务部职责1、对公司的财务管理负全责,具体负责公司日常财务管理及核算工作。2、根据公司资金运作情况合理调配资金,确保公司资金正常运转;3、搜集公司经营活动情况、资金动态、营业收入和费用开支的资料并进行分析、提出建议,定期向总经理报告;4、组织编制公司月、季、年度营业计划和财务计划,对资金运作情况进行检查和分析;5、严格财务管理、加强财务监督,督促财务人员严格执行各项财务制度和财经纪律;6、负责公司各项财产的登记、核对、抽查和调拨,按规定计算折旧费用,保证资产的来去分明;7、了解公司所有对外经济合同的内容;8、负责公司现有固定资产管理工作;9、会计意见反映及督促,税务及税法研究;10、完成领导交办的其他任务。四、工程技术部职责1、工程技术部立足于信息系统维护与新项目开发;2、立足行业客户软件定制开发;3、在项目经理带动下,实施项目;4、系统维护以及内部网的开发和维护;5、公司信息化建设的其它工作。
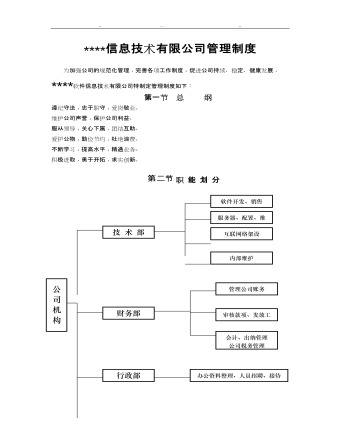
公司管理制度(适用于信息技术公司)
员工守则一、公司全体员工必须遵守公司的各项规章制度和决定。二、凡事以公司利益为重,有集体荣誉感。禁止任何部门、个人做有损公司利益、形象、声誉或破坏公司发展的事情。三、员工在上班时间应保持仪表整洁,举止端庄,行为检点,谈吐得体。特别在代表公司对外业务联系时应树立公司良好形象。四、员工应发扬求真务实的工作作风,提高工作效率;团结互助,同舟共济,发扬集体合作和集体创造精神,增强团体的凝聚力和向心力。在工作当中应多发挥主观能动性,为公司出谋划策,多提合理化建议。各部门、各员工之间应互相配合,真诚协作,互相信任,互相学习,同心协力解决问题;注重对工作的主动性及创造性的培养,提高工作效率,不断提高个人的自身素质,每位员工都应尽职尽责,一切工作为求做到最好的效果。五、员工必须服从公司的组织领导与管理,对上级领导安排的工作应按质按量地完成,对未经明示事项的处理,应及时请示,遵照指示办理;员工必须尽职尽责、精诚合作、敬业爱岗、积极进取。六、每位员工都有义务爱护公司财产,遵守公司关于设备使用的规定。管理、保养好所使用的设备并使之处于完好状态。损坏或遗失公司财物要立即报告上级,并主动赔偿由本人原因造成的全部或部分损失。不得将公司的财物据为已有。未经允许,不得随意翻看其它同事或公司的物品和资料。七、节约就是美德,节约就是利润。从自身做起,从节约一张纸、一滴水、一度电、一分钱做起,反对浪费。八、维护公共环境卫生,随时保持办公区域的整洁,个人的办公桌和办公用品要每天整理,垃圾应扔到垃圾篓,不得随地吐痰,乱抛杂物、纸屑果皮等;七、上班时间应保持良好的工作气氛及环境,严禁打闹、嬉笑、高声喧哗、吃零食、看小说及与专业无关的报刊、杂志;不得利用公司电脑打游戏、聊天或做其它与工作无关的事情。办公室内严禁打牌、下棋,酗酒、吸烟等。

公司管理制度(适用于信息技术公司)
一、董事会职责1、负责召集股东会,并向股东报告工作;2、执行股东会的决议;3、审定公司的经营计划和投资方案;4、制订公司的年度财务预算方案;5、制订公司的利润分配方案和弥补亏损方案;6、制订公司增加或者减少注册资本方案;7、拟订公司合并、分立、变更公司形式、解散的方案;8、决定公司内部管理机构的设置;二、综合管理部基本工作职责1、行政事务:⑴ 拟定公司行政管理制度并监督实施;⑵ 公司会议管理;⑶ 档案管理;⑷ 印章管理;⑸ 合同管理;⑹ 办公设备及办公用品采买和管理;⑺ 车辆管理;⑻ 消防、安全卫生管理;⑼ 资产管理;⑽ 公司经营所需的各种信息资源管理;⑾ 公司对外关系管理;⑿ 公司各项年检工作;⒀ 企业文化建设及企业形象策划;⒁ 完成总经理及副总经理交办的其他任务。2、人事管理事务:综合管理部的人事职责是负责公司各级员工的聘用、考核、监察、调动、离职、社会保险等。具体职责如下:⑴ 组织拟定公司各机构的人员编制计划;⑵ 负责公司各职位薪酬规划、福利制度制订与修订;⑶ 负责公司人员选聘、考核、监察、调动等工作;⑷ 对拟招聘的公司人员进行面试调查,并办理有关入职手续;⑸ 办理人员任免、调薪、迁调、奖惩等各项事务;⑹ 负责公司员工劳动合同、社会保险、请假等工作;⑺ 定期组织对员工的考核、评议;⑼ 员工考勤管理及劳动纪律管理;⑿ 负责落实执行公司的各种规章制度;⒀ 完成领导交办的其他任务。三、财务部职责1、对公司的财务管理负全责,具体负责公司日常财务管理及核算工作。2、根据公司资金运作情况合理调配资金,确保公司资金正常运转;3、搜集公司经营活动情况、资金动态、营业收入和费用开支的资料并进行分析、提出建议,定期向总经理报告;4、组织编制公司月、季、年度营业计划和财务计划,对资金运作情况进行检查和分析;5、严格财务管理、加强财务监督,督促财务人员严格执行各项财务制度和财经纪律;6、负责公司各项财产的登记、核对、抽查和调拨,按规定计算折旧费用,保证资产的来去分明;7、了解公司所有对外经济合同的内容;8、负责公司现有固定资产管理工作;9、会计意见反映及督促,税务及税法研究;10、完成领导交办的其他任务。四、工程技术部职责1、工程技术部立足于信息系统维护与新项目开发;2、立足行业客户软件定制开发;3、在项目经理带动下,实施项目;4、系统维护以及内部网的开发和维护;5、公司信息化建设的其它工作。五、产品研发部职责1、负责新产品的研制开发、引进及消化吸收;2、现有产品的改进;3、对公司内外相关部门提供技术服务和技术支持;4、做好各类技术信息和资料收集、整理、分析、研究汇总、归档保管工作,为逐步实现公司现代化销售的目标,提供可靠的指导依据;5、负责制定公司产品的企业统一标准,实现产品的规范化管理;6、及时指导、处理、协调和解决产品出现的技术问题;7、负责编制公司技术开发计划,抓好技术管理人才培养,技术队伍的管理。有计划的推荐引进、培养专业技术人员,搞好业务培训和管理工作;

软件技术人员外包服务合作框架协议
(以下简称甲方),与(以下简称乙方) 就乙方愿意成为甲方的签约外包服务供应商,为甲方提供技术人员外包服务,双方本着平等互利的原则,根据《中华人民共和国合同法》、《中华人民共和国民法通则》及其他相关法律、法规,本着诚实守信的原则,经友好协商,同意按下列条款签订本协议及相应附件,并共同遵守。第一条软件技术人员外包服务合作框架协议(以下简称本协议),本协议的附件构成本协议不可分割的一部分,本协议包括以下附件:附件一 外包服务的内容、规范与付费标准;附件二 技术服务补充协议——人员名单及使用期限;附件三 人员考核、考勤及工作规范要求;附件四 人员考勤记录单;附件五 人员考核记录单;本协议为外包服务之人员派遣框架协议,甲乙双方合作只需要签署本协议即可开展工作。第二条外包服务的具体内容、规范与付费标准详见附件一。乙方根据甲方需求确定附件二中的人员单价与服务期限,服务完成后或到三个月的结算期后根据考核与考勤再次确认具体支付费用。甲方需要终止或暂停某个人员的服务需要提前十五日以书面或邮件形式通知乙方,乙方有权将终止或暂停的相关服务人员派遣到别的项目组服务。合同期内,甲方可以根据需要增加工程师,乙方接到请求后十五日内安排到位。增加的工程师双方以附件二的形式进行确认。

提供数据处理专业技术服务合同书
一、合同标的1.1乙方同意向甲方提供、甲方同意接受乙方提供本合同项下所列的专业技术服务(以下简称专业服务)。 1.2 一方未获另一方事先书面许可,不得将本合同所述的权利、义务及/或责任转让予第三方。1.3 乙方需将本合同项下的专业技术服务项目分包其他方提供时,应在本合同规定的项目启动前30个工作日,以书面形式通知甲方,甲方同意后双方签署合同变更书,方可生效。否则,甲方有权视分包商提供的服务为无效服务。1.4 《专业技术服务说明书》应确定乙方提供的专业技术服务项目、专业技术范围、服务实施前提、工作项目、乙方及甲方责任、服务水准、专业技术服务完成标志以及提供专业技术服务的时间。1.5 《专业技术服务说明书》服务项目中每一项服务完成时,双方将依照双方共同约定的验收方式和标准进行验收后,签署《验收备忘录》。

转让技术秘密和补偿贸易合作生产合同
第一条 技术名称、资料1.技术名称、权属: 2.“技术文件资料”的定义、范围及交付: (1)一般技术资料包括: (2)产品设计图纸: (3)生产技术资料: (4)资料的修改: (5)资料的提供方式: a.对一般技术文件应提供三份蓝图或同等数量的清晰的复制图;b.对产品设计图纸应提供一份生产底图及两份蓝图;c.对生产技术资料应提供两份蓝图;d.对已提供过的完全相同的重复资料,可免于提供,但需在清单中予以注明。(6)资料的交付进度: a.根据资料定义的规定,在签订合同后30天需交付合同产品的全部技术资料和图纸;b.根据资料定义的规定,在签订合同后于 年 月 日前需向 交付合同产品的全部技术资料和图纸。第二条 合作期限1.以补偿贸易进行使用生产期限为2年,2年后若合资经营条件不成熟,则可延长合作生产期限,但最长不得超过5年。

【高教版】中职数学拓展模块:3.4《二项分布》教案设计
教 学 过 程教师 行为学生 行为教学 意图时间 *揭示课题 3.4 二项分布. *创设情境 兴趣导入 我们来看一个问题:从100件产品中有3件不合格品,每次抽取一件有放回地抽取三次,抽到不合格品的次数用表示,求离散型随机变量的概率分布. 由于是有放回的抽取,所以这种抽取是是独立的重复试验.随机变量的所有取值为:0,1,2,3.显然,对于一次抽取,抽到不合格品的概率为0.03,抽到合格品的概率为1-0.03.于是的概率(仅求到组合数形式)分别为: , , , . 所以,随机变量的概率分布为 0123P 介绍 播放 课件 质疑 了解 观看 课件 思考 引导 启发学生得出结果 0 10*动脑思考 探索新知 一般地,如果在一次试验中某事件A发生的概率是P,随机变量为n次独立试验中事件A发生的次数,那么随机变量的概率分布为: 01…k…nP…… 其中. 我们将这种形式的随机变量的概率分布叫做二项分布.称随机变量服从参数为n和P的二项分布,记为~B(n,P). 二项分布中的各个概率值,依次是二项式的展开式中的各项.第k+1项为. 二项分布是以伯努利概型为背景的重要分布,有着广泛的应用. 在实际问题中,如果n次试验相互独立,且各次实验是重复试验,事件A在每次实验中发生的概率都是p(0<p<1),则事件A发生的次数是一个离散型随机变量,服从参数为n和P的二项分布. 总结 归纳 分析 关键 词语 思考 理解 记忆 引导学生发现解决问题方法 20

人教版高中语文必修3《劝学》教案2篇
五.研习第一段:1.诵读指导要处理好句中停顿2.请学生对照注释翻译本段重点词句:学不可以已已:停止。青,取之于蓝而青于蓝于:从;比。木直中绳中:zhàng符合,合于。虽有槁暴,不复挺者,揉使之然也有通又,揉通煣,以火烘木,使其弯曲。然:这样。翻译:故木受绳则直,金就砺则利,君子博学而日参省乎己,则知明而行无过矣。所以木材经墨线画过(再用斧锯加工)就直了,金属刀剑拿到磨刀石上(磨过)就锋利了,君子广博地学习并且每天对自己检验反省,就能智慧明达,行为没有过错了。3.本段是从哪个角度论述中心论点的?明确:本段是从学习的意义这个角度论述中心论点的。荀子认为人的知识、道德、才能都不是天生成的,而是后天不断学习获得的,学习的意义十分重大,所以学习不能停止。4.本段中几个比喻句是为了说明什么道理?学生讨论发言,教师明确:

人教版高中历史必修3宋明理学教案2篇
二、程朱理学:1、宋代“理学”的产生:(1)含义:所谓“理学”,就是用“理学”一词来指明当时两宋时期所呈现出来的儒学。广义的理学,泛指以讨论天道问题为中心的整个哲学思潮,包括各种不同的学派;狭义的理学,专指程颢、程颐、朱熹为代表的,以“理”为最高范畴的学说,称为“程朱理学”。理学是北宋政治、社会、经济发展的理论表现,是中国古代哲学长期发展的结果,是批判佛、道学说的产物。他们把“理”或“天理”视作哲学的最高范畴,认为理无所不在,不生不灭,不仅是世界的本原,也是社会生活的最高准则。在穷理方法上,程颢“主静”,强调“正心诚意”;程颐“主敬”,强调“格物致知”。在人性论上,二程主张“去人欲,存天理”,并深入阐释这一观点使之更加系统化。二程学说的出现,标志着宋代“理学”思想体系的正式形成。【合作探究】宋代“理学”兴起的社会条件:

